一题看尽长安花*——2018年全国高考数学Ⅰ卷文21题的多证

广东省惠州市第一中学 (516007) 郭煜辉

有关导数压轴题一直是高考研究的热点.与往年相比，2018年的文科导数题少了一份彷徨，多了一分亲切.初次尝试，使人兴趣盎然；细细体会，让人意犹未尽；再三品味，解法多种，欲罢不能.可从这一道题，展现出证明导数不等式的多种常用解题思路.

一、题目

评注：本题与2016年广州一模文科压轴题几乎如出一辙，让人倍感亲切.哪怕没有做过，但本题的函数是考试中最常见的“ex”与“lnx”的结合，对考生而言，实在是“最熟悉的陌生人”.

二、解法分析

评注：本解法单刀直入，进行放缩，构造出形式较简单的函数.但学生较难掌握放缩的度，普遍对放缩法存在畏惧，学生反而不易想到.

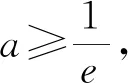
评注：当需要求解参数取值范围时，优先考虑将式子参变分离，得到平行于x轴的函数图像y=a，容易画图解决问题.本题中，经参变分离后的函数表达式结构不复杂，对分子进行二次求导求最值点.

评注：本题采用虚设零点的解法，即在导数问题中，遇到导函数有零点，但无法求出时，则可将零点只设不求，利用一阶导数为零的等式，在原函数中进行整体代换.其步骤有三：(1)构造合适的可导函数(若原函数结构复杂，可将一阶导数的局部函数构造新函数)；(2)利用零点存在性定理，判定一阶导函数零点的大致位置，寻找到使函数值一正一负的区间；(3)利用方程f′(x)=0为零，用x0或含x0的式子进行整体代换，转化成便于求最值的函数.

本题运用这种解法的关键，是能挖掘出存在零点.解题中有2处难点：一是利用极限探求出零点的大致位置；二是利用一阶导数为零的方程整体代换.本题为虚设零点的解法作出了很好的示范.

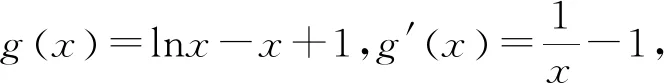
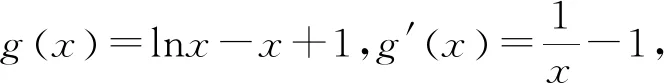
评注：解法四和解法五中的不等式“ex≥x+1”和“lnx≤x+1”是函数不等式中的重要结论.课本中该不等式并没有以定理形式呈现的，所以在规范性的答题中结论还需先证明，再使用.

解法六：由于a·ex-lnx-1≥0⟺a·ex≥lnx+1，令h(x)=lnx+1，过(0,0)作切线为y=kx，设切点为(x0,y0)，

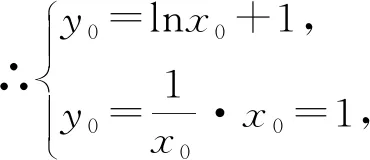
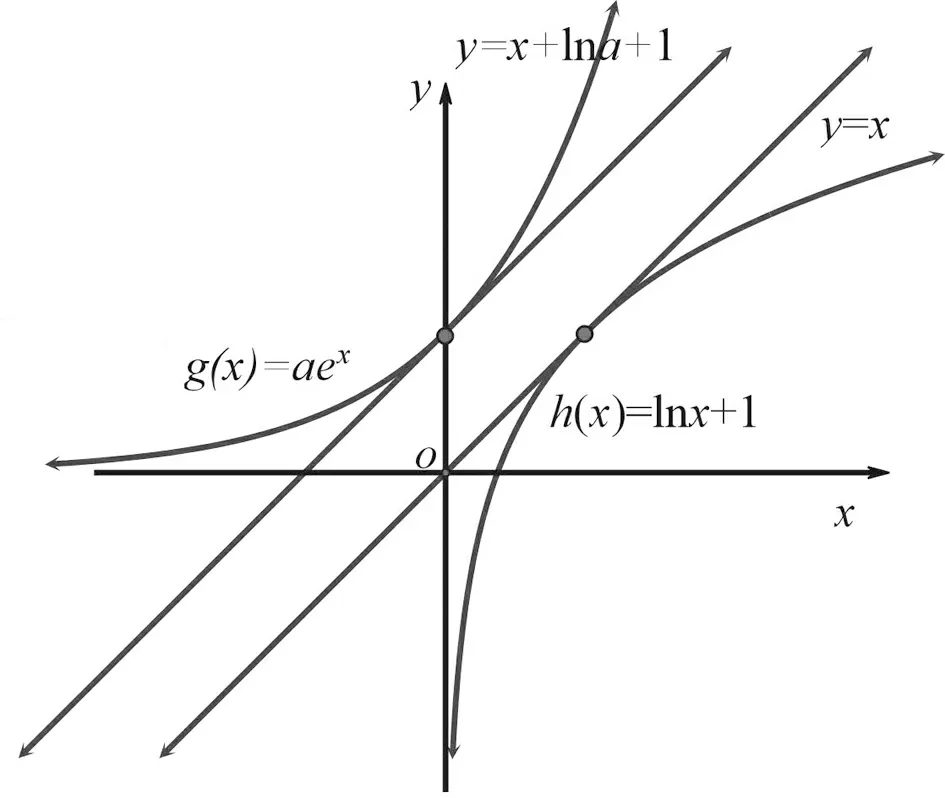
图1

评注：构造切线比较大小，是利用函数图象的几何意义证明不等式，是证明不等式的常用手段.本解法恰是对法四在几何意义上的具体运用：即y=ex的图象在切线y=x+1之上(y=lnx的图象在切线y=x-1之下).

在比较大小的题目中，往往寻找中间量进行对比，得出大小.本解法恰恰是以切线作为中间量，通过对比两条切线的位置，比较得出.此法也可理解为对法一放缩法的几何运用.(放缩成切线对比.)

本解法步骤主要有三步：(1)寻找易于求切线的点(对数函数常找(0,0)、(0,1)，指数函数常找(1,0))，过该点求出已知曲线的切线；(2)利用平行关系，求出另一函数的平行切线；(3)把两切线作为中间变量，对比两者位置关系比较大小.

高考试题都是匠心之作，是核心素养和数学知识的综合载体.除具备选拔功能，也具备良好的教学功能.作为教师，不仅仅需要解题，更需要对问题深入探究，挖掘出隐藏在题目中的内涵，找到解决问题在思想和方法上的共性.研究高考试题亦是把握高考方向的重要途径.从2019、2020年的高考命题规律来看，导数题难度下降，已不再是压轴题的必然选择.回头来看，2018年的这道文数21题，亦像是对以往导数压轴题的致敬，集通法于一身，为日后高三的导数复习，作出示范和铺垫.