构造函数法求解导数题中的不等问题
浙江省嘉兴市秀水高级中学 (314000) 冯雪莲
解决导数中的不等问题有很多的方法,而通过构造函数,利用求导数解决问题就是一个非常有效的方法,本文中通过分析、点评几个典型题例,介绍此法在解题中的一些运用方法和解题体会,希望能对读者朋友有所帮助.
一、求不等式的解
此处的不等式是通过求导判断某函数的单调性来解的.
例1 已知函数的定义域为R,f(-1)=2,对任意x∈R,f′(x)>2,则f(x)>2x+4的解集为.
解析:设g(x)=f(x)-2x-4,由f′(x)>2得g′(x)=f′(x)-2>0,于是g(x)是R上的增函数,又由f(-1)=2得g(-1)=f(-1)+2-4=0,由f(x)>2x+4得g(x)>0=g(-1),所以有x>-1.
评注:本题中解决问题的关键是如何利用给出的导数条件为解不等式服务,通过构造一个与它们都有联系的函数化解了难点,此处新构造一个函数是解题的最重要的环节.
例2 已知定义在R上的函数f(x)满足f(1)=2,f′(x)<1,则不等式f(x2) 解析:由于f′(x)<1,则f′(x)-1<0,设g(x)=f(x)-x+C(C为常数),则g′(x)=f′(x)-1<0,所以g(x)是单调减函数,由f(1)=2知g(1)=f(1)-1+C=1+C,由于f(x2) 评注:此题虽然也是解不等式问题,但破解函数的复合环节也比较重要,如果按照例1的方法直接构造与欲解不等式相关的函数会遇到很多的麻烦. 通过构造函数将需要比较的两式大小问题转化为求函数最值问题. 例3 已知f(x)=xlnx,g(x)=-x2+ax-3,若对一切x∈(0,+∞),2f(x)≥g(x)恒成立,试确定实数a与4的大小. 评注:此题是用分离变量法解题的典型题目,a≤h(x)恒成立就是a≤h(x)min,a≥h(x)恒成立就是a≥h(x)max,这里要注意变量分离时的等价性. 例4 设函数f(x)在R上的导函数为f′(x),且2f(x)+xf′(x)>x2,试比较f(x)与0的大小. 解析:由2f(x)+xf′(x)>x2知:当x=0时,f(0)>0;当x>0时,不等式两边同乘以x,则2xf(x)+x2f′(x)>x3>0,即(x2f(x))′>0,设h(x)=x2f(x),则h′(x)<0,所以h(x)在(0,+∞)上单调递增,又h(0)=0,故h(x)=x2f(x)>0,于是f(x)>0;当x<0时,不等式两边同乘以x,则2xf(x)+x2f′(x) 评注:通过抓住题意,利用两式积的函数的求导法则构造出函数h(x)=x2f(x),通过分类讨论机智地解决了大小的判断,有根有据,推理顺畅. 先将待证的不等式转化为一个函数不等式,然后利用求导方法解题. 例5 已知实数a>ln2-1,当x>0时,证明:ex>x2-2ax+1. 证明:设f(x)=ex-x2+2ax-1,则f′(x)=ex-2x+2a,再设g(x)=ex-2x+2a,则g′(x)=ex-2,当x∈(0,ln2)时,g′(x)<0;当x∈(ln2,+∞)时,g′(x)>0,所以[g(x)]min=g(ln2)=2-2ln2+2a,由a>ln2-1得[g(x)]min>0,即f′(x)>0,于是f(x)是单调增函数,则当x>0时,有f(x)>f(0)=0,即ex>x2-2ax+1. 评注:通过构造函数,将证明不等式转化为求函数最值问题,经过两次求导数,利用函数单调性解决了判断问题,这是求相关导数综合题中的常见方法. 评注:题中针对x∈N*的重要特征,机智地将要证明的不等式f(x)≤x-1,转化为证明1+ln(x-1)≥x-1,破解了解题难点,简化了解题过程. 通过求某函数的最值构造不等式或者对参数分段讨论解决. 例7 已知函数f(x)=(a+1)lnx+ax2+1,设a<-1,若对任意x1,x2∈(0,+∞),都有|f(x1)-f(x2)|≥4|x1-x2|,求a的取值范围. 评注:解题时先根据函数f(x)的单调性,将已知不等式转化为另一个函数的单调性问题,再由导数列出不等式,然后得到参数范围,整个解题过程设计精巧,令人耳目一新. 例8 已知f(x)=ae2x+(a-2)ex-x.若f(x)有两个零点,求a的取值范围. 评注:解题中的取点过程用到了放缩的技巧,而完成大小比较时是通过两次建立函数,然后再求导、判断单调性、求值解决的,充分体现了函数的解题作用.二、判断大小

三、证明不等式

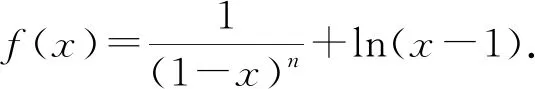
四、求参数范围