HPM视角下深度学习课例开发
——以点到直线距离公式再证明为例
甘肃天水市一中 (741000) 文贵双
浅层学习以知识获取和记忆训练为主要特征,学习处于相对较低的认知水平;深度学习则以知识深度加工、意义建构和深度思维为主要特征,以理解、应用、分析、推理、综合、评价、创造等高层次认知活动为主要学习活动,学习处于高认知水平.深度学习是一种主动的、探究式的、有意义的学习过程,是深入内容本质的概念理解、知识探究、问题解决等相对复杂的学习过程,学生能够将学到的知识迁移与应用,实现知识的深层加工、深刻理解以及长久保持,并实现“高层次认知能力”和“高阶思维”的发展,促进深刻理解的同时帮助他们把握学习内容的核心与联系.
怎样让学生进入深度学习的状态?郭华教授认为,在教师引领下,教学中围绕具有挑战性的主题,引导学生围绕学习内容深入思考、积极对话,表达与展示自己的思维过程,形成深层次的认知参与和积极的情感体验.而挑战性的主题哪里来?HPM案例就是深度学习的好素材.
HPM(数学史与数学教育)中的历史发生法就是通过数学史料的研究,发现数学对象和数学思维的发生发展规律,为解决数学教学的现实问题提供历史的借鉴和支持.因为任何数学知识都是人类数学认识不断建构的结果,从简单到复杂,从直观到抽象,从经验概括到形式构造,经历漫长的历史过程,这是数学家或几代数学家独特而深邃的高级思维方式的成果.他们的高级思维过程是学生进行思维活动的典范,他们的思维通过教师的加工处理来示范引导学生的深度学习.本人在高三复习交流会上上了一节“点到直线距离公式的再证明”的观摩课,示范借力HPM来引领学生深度学习,引起大家的热评.
1 课堂实录
师:我们在高一学习了点到直线的距离公式,由于当时受到所学知识的限制,该定理的证明方法单一,现在我们已经学完了高中数学全部内容,掌握了许多工具,今天我们再证“点到直线的距离公式”,公式如下:

1.1 再现教材公式的推导过程


图1

哪位同学得到启发?


图2
师:19世纪末,英国数学家约翰斯顿(W.J.ohnston),将点线距离转化成三角形的高,其证明和上面证法一样.下面我们从不同的视角探讨其他证法.
1.2 多视角寻找证法,培养学生思维的发散性

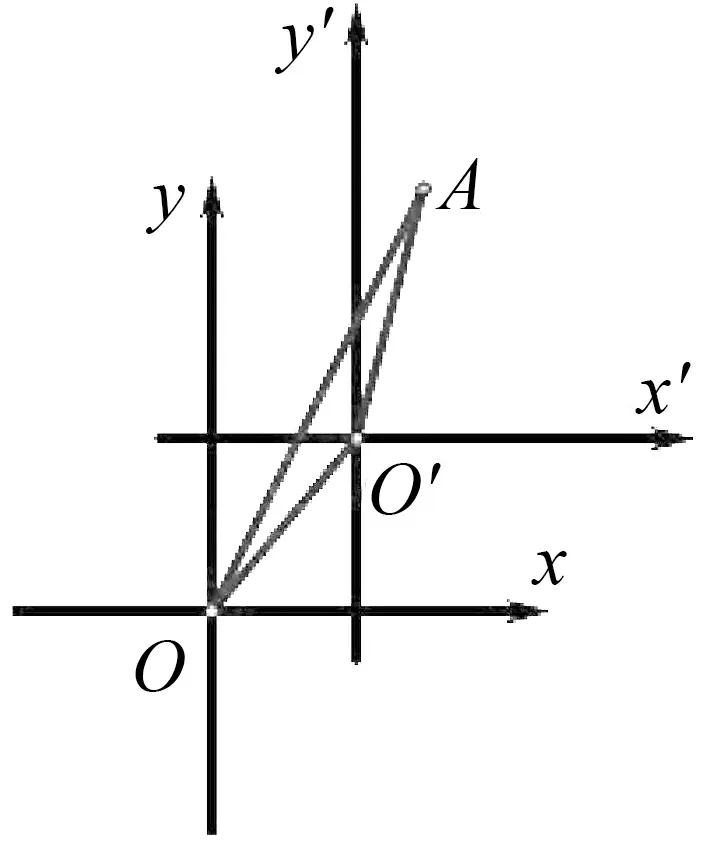
图3
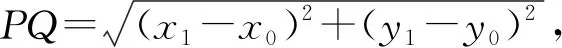
生:我有一个不需求Q的坐标的证法.

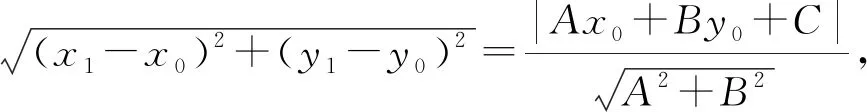

师:不错,回到点线距离的定义,配凑出目标.19世纪的英国数学家杨格(J.R.Young)是从方程组中解出(x1-x0),(y1-y0),代入距离公式得到公式.到了20世纪,有人在杨格的基础上采用设而不求的方法,将方程组两边平方,从而简化了运算,和本解法一样.
生:类比斜面上物体受力分析图,本题作如图4的图形,直角△PQM中,∠QPM等于直线的倾斜角或其补角.
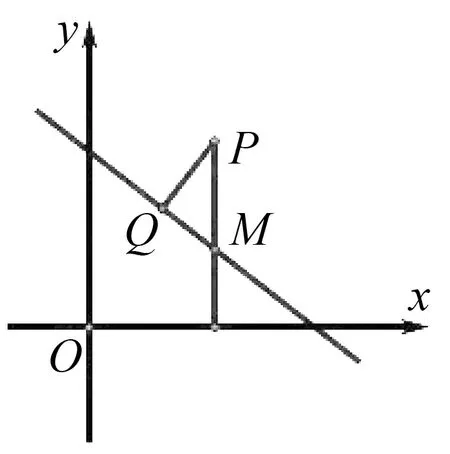
图4

师:这个证明与19世纪英国著名数学家托德亨特(I.Todhunter)证法一样,真是英雄所见略同.
生:受到空间向量求点到面距离的启发,可以用向量证明.
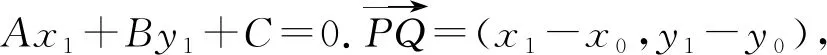
师:20世纪40年代,向量知识逐渐出现在西方教科书中,教科书的编者给出了这样的证法.
生:由于点P到直线l的距离是点P到直线l上任意一点距离的最小值,故可以得出目标函数,利用二次函数的最值求得点P到直线l的距离公式,但推导比较复杂.
师:想法自然,但运算复杂.把展示的机会留给老师啊,老师提供如下证法:

20世纪,美国数学家泰勒(A.E.Taylor)在其《微积分与解析几何》著作中提供上述证法.抓住距离概念的本质,巧用柯西不等式是难点.
星移物换,穿过浩渺的时空,发现古代数学家们的证法与我们的相同,为同学们的聪明才智点赞.
2 结语
《普通高中数学课程标准》指出,定理教学的意义不仅在于学生掌握“书本知识”,更重要的是让他们从中体验数学家概括数学定理的心路历程,通过典型问题的设置和学生的探索,使学生理解定理逐步形成的过程,体会蕴含在其中的思想,追寻数学发展的历史足迹.然而实际教学中,教师通常为了挤出时间多做练习,“轻松”地给出定理,学生失去了“自主探索定理产生的背景及蕴含的思想,亲身经历定理的发生、发展的过程”,失去了“深刻体验、直观感知、观察发现、抽象概括、归纳类比、反思与建构等思维历程”,失去了提升学生核心素养的大好时机.加之,学生学习受内容的制约,后续学习的方法用不到定理的证明中,这就需要我们在恰当的时间点,把定理放在更大的系统中,根据学生学习的不断深入,对定理(公式)二度认识,从不同的角度推导证明.本节课所有的证法只要教师启发得当,学生全身心投入探究,大家合作交流都能发现,教师不失时机说明这是历史上那位数学家的证法,并对学生赞扬,使学生产生成果的喜悦,增强学习的兴趣.这正是华东师大汪晓勤教授提出的,数学史融入数学教学六种教育价值:知识之谐、方法之美、探究之乐、能力之助、德育之效、文化之魅.
美国著名数学家和数学史学家M·克莱因认为,历史上数学家遇到的困难和挫折,课堂上同样学生也会遇到,因而历史对于课堂教学具有借鉴和指导作用.教材往往按照数学知识的逻辑体系进行编写,而这种逻辑体系下的知识呈现与知识的历史真实发生过程往往不一样,在这样的过程中学生很难体会到数学家的思维历程,学生的思维完全被老师的讲解所代替,学生的认知是低水平,思维得不到最大的优化,因此,在教学中我们可以适当借用HPM案例展示数学家如何思考问题,在遇到困难时如何选用合适的思维方式解决问题,让学生感受到数学家的卓越智慧,学习他们研究数学问题的思维方式方法.

