建构两类基本模型 突破电学教学难点

摘 要：建构模型是解决物理问题的重要方法，在电学中建构两类基本模型，能有效解决电学中电表示数变化、电路故障、误差分析、动态电路和安全电路的计算、设计电路等系列难题.本文主要阐述教师如何在教学中通过建构两类基本模型并对其进行变式训练，帮助学生深化理解电学内容.

关键词：物理模型;电学;教学难点

中图分类号：G633.7 文献标识码：B 文章编号：1008-4134（2021）08-0033-03

基金项目：江苏省教育科学“十三五”规划课题“指向物理学科核心素养的‘单元设计”（项目编号：R-c/2016/07）.

作者简介：吉临荣（1966-），男，江苏海安人，本科，中学正高级教师，江苏省特级教师，物理教研员，研究方向：低成本实验和中考评价的研究.

电学是初中物理的教学难点，由于电学内容公式多、方法多、题型多，因此导致教师怕教，学生难学.笔者潜心研究电学试题，发现在教学中建构两类基本模型，并通过对其进行变式练习、拓展提升，能解决一系列电学难题，有效突破电学教学难点.现举例说明如下.

1 建构两类基本模型

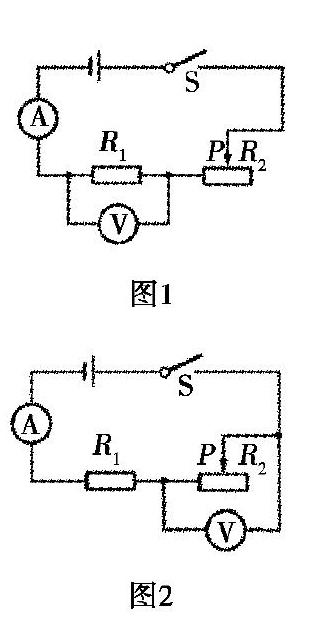
模型一：如图1所示，当滑动变阻器滑片P向左滑动时，电流表示数，电压表示数（选填“变大”“不变”“变小”）.

解析：当P向左滑时，电阻R2阻值变小，电路中总电阻R阻值也变小，根据欧姆定律I=U/R可知，当电源电压U不变时，电路中电流I变大，即电流表示数变大;又由于电阻R1阻值不变，所以其两端电压U1变大，即电压表示数变大.

模型二：如图2所示，当滑动变阻器滑片P向左滑动时，电流表示数，电压表示数（选填“变大”“不变”“变小”）.

解析：当P向左滑时，同理可推知电流表示数变大;再用欧姆定律I=U/R分析，R2两端电压U2=I2R2，由于电流I2变大，电阻R2阻值变小，所以电阻R2两端电压U2无法判断.

电学题的分析思路一般有三种：一是利用欧姆定律分析，如上述分析;二是利用串联或并联电路特点分析，根据U2=U-U1可知，电源电压U不变，而电阻R1两端的电压U1变大，所以电阻R2两端的电压U2变小，即电压表示数变小;三是利用串联分压或并联分流规律分析，电阻R2阻值变小，其两端分得的电压也随之变小.

归纳：模型一有“定阻电流电压同向变”， 模型二有“变阻电流电压反向变”.

2 变式练习、拓展提升

变式1：（扬州中考题）如图3甲所示，R2为酒精气体传感器，其阻值随酒精气体浓度的变化曲线如图3乙所示，当酒精气体浓度增大时，电流表示数，电压表示数.

解析：此题R2是一只酒精气体传感器，其阻值随酒精气体浓度的变化曲线如图3乙所示.也就是当酒精气体浓度变化时，其阻值也相应发生变化，起到滑动变阻器的作用，由于电压表测量定值电阻R1的阻值，所以此题属于模型一.

由图3乙可知，当酒精气体浓度增大时，电阻R2阻值变小，电流表示数变大，学生直接利用模型一的归纳结论便可以得出电压表示数也变大.

變式2：（宿迁中考题）如图4所示为油量表（由电流表改装而成）电路，当油面上升时，油量表示数，电压表示数.

解析：此题R2是一只滑动变阻器，由于电压表测量的是变化电阻R2的阻值，所以此题属于模型二.

由图4可知，当油量上升时，浮标也上升，在杠杆的作用下电阻R2的滑片向下移动，电阻R2阻值变小，电流表示数变大，学生直接利用模型二的归纳结论就可以得出电压表示数变小.

变式3：（徐州模拟中考题）小红设计了测量某定值电阻的阻值实验，通过改变滑动变阻器的电阻大小，测量并记录了多组电压表和电流表的读数，根据表格中记录的数据分析，小红所连接的电路可能是下列电路图中的哪一个.

解析：此题由表格中的数据分析可知，当电压增大时，电流反而减小，这是模型二的电表示数变化的特征，也是模型二归纳结论的逆向运用.由此可知电压表错接在滑动变阻器两端，所以本题选A选项.

变式4：（山东菏泽中考题）小军采用如图6所示的电路，研究“通过某导体的电流与它的电阻关系”，他分别用5Ω和10Ω的电阻做两次实验，当完成第一次实验后，小军将A、B两点间的电阻R由5Ω更换为10Ω，闭合开关后，滑动变阻器应该

A.保持滑动变阻器滑片不动

B.将滑动变阻器滑片向右移动

C.将滑动变阻器滑片向左移动

D.更换阻值更大的滑动变阻器

解析：当A、B两点间的电阻R由5Ω更换为10Ω，说明电阻R在变化，而电压表接在电阻R两端，因此本题属于模型二.当电阻R变大时，电路总电阻也变大，电流表示数变小，直接利用模型二归纳的结论得出电压表示数变大.

而研究“通过某导体的电流与它的电阻关系”时，必须要控制电阻R两端电压不变，而且电阻R已换为10Ω，所以只好改变滑动变阻器的电阻，也就是说本题此时又属于模型一.要将电压表示数减小，直接利用模型一归纳的结论逆向推理可知电流表示数也要减小，滑动变阻器的电阻要变大，即将滑片向右滑，因此选择B选项.

变式5：（黄冈中考题）如图7所示电路中，电源电压保持不变，R为定值电阻，当在a、b两点间接入一个“6V 2W”的小灯泡时，小灯泡恰好正常发光;若换一个“6V 3W”的小灯泡，则这个小灯泡

A.比正常发光暗些

B.比正常发光亮些

C.仍能正常发光

D.灯丝将被烧坏

解析：当在a、b两点间接入一个“6V 2W”的小灯泡时，小灯泡恰好正常发光，说明a、b间的电压大小是6V.将“6V 2W”的小灯泡换成“6V 3W”的小灯泡时，从电阻阻值角度思考，实质上是将阻值为18Ω的电阻换成阻值为12Ω的电阻，在此基础上分析a、b两点间的电压，此题就可转化为模型二来分析.

当电阻Rab变小时，电路总电阻也变小，电流表示数变大，直接利用模型二归纳的结论得出Uab变小，此处的小灯泡比正常发光暗些.

变式6：如图8所示，如果在电阻R1两端并联一只电阻R3，电流表示数，电压表示数.我们知道电压表是有电阻的，当它并联在电阻两端测电压时，对原电路会造成一定的影响.如图9所示，当电压表并联到R1两端时，测出的电压值与未接入时相比较要（选填“变大”或“变小”）.

解析：在R1两端并联一只电阻R3，电阻R1与R3并联后的总电阻变小，相当于电压表间的电阻变小，此题属于模型二.

当电阻R1和R3并联，并联的总电阻变小时，电路总电阻也变小，电流表示数变大，直接利用模型二结论得出电压表示数变小.

考虑到电压表有电阻，因此电压表便相当于图8中的电阻R3，这样图9就等效于图8，当电压表并联到R1两端时，测出的电压值与未接入时相比较要小.

变式7：（兰州中考题）在如图10所示的电路中，电阻R1=8Ω，R2=10Ω，电源电压及定值电阻R的阻值未知.当开关S接位置1时，电流表示数为0.2A.当开关S接位置2时，电流表示数的可能值在A到 A之间.

解析：开关S接2时与接1时比较，电阻由8Ω增大为10Ω，电路中电流应变小，即电流表示数小于0.2A，此题也就转化为模型二来思考.

直接由模型二归纳的结论得，电阻R2两端的电压应变大，由欧姆定律得原来电阻R1两端电压为U1=IR1=0.2A×8Ω=1.6V，所以U2>1.6V，I=I2=U2/R2>1.6V/10Ω=0.16A.电流的可能值在0.16A到0.2A间.

变式8：如图11所示，滑动变阻器的滑片在某两点间移动时，电流表的示数范围为1A到2A之间，电压表的示数范围为6V到9V之间.试求：定值电阻R的阻值及电源电压.

解析：如图11所示，属于模型二，也就是电流表的示数与电压表的示数应为反方向变化.

而题设条件是“电流表的示数范围为1A到2A之间，电压表的示数范围为6V到9V之间”，它们正确的对应关系是“当电流为1A时，电压表示数为9V;当电流为2A时，电压表示数为6V”.

根据电源电压相等，可列方程为：I1R+U1=I2R+U2，即1A·R+9V=2A·R+6V，解得R=3Ω，进而得U=1A×3Ω+9V=12V.

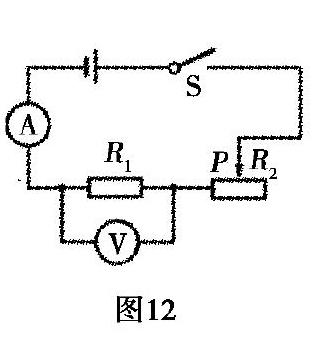
变式9：在如图12所示的电路中，电源电压保持不变.电路中滑动变阻器上标有“20Ω 2A”字样，电流表的量程为0-0.6A，电压表的量程为0-3V，电阻R1的阻值为4Ω.当滑片在滑动变阻器的最右端时，闭合开关，电压表的示数为1.5V，求：

（1）电源电压.

（2）为了保证电路能正常工作及各电表不致损坏，滑动变阻器的取值范围.

解析：（1）U=U1+U2=U1+I2R2=U1+U1/R1·R2=1.5V+1.5V/4Ω×20Ω=9V;

（2）由图12可知，此题属于模型一，电流表和电压表示数同方向变化.

当滑动变阻器的阻值变小时，电流表示数变大，电压表示数也变大，当I=0.6A时，U1max=I1R1=0.6A×4Ω=2.4V;Rmin=U2min/Imax=（U-U1max）/Imax=（9V-2.4V）/0.6A=11Ω.

当滑动变阻器阻值变大时，电流表示数变小，电压表示数也变小，电流表和电压表都安全，电阻R2最大值为20Ω.所以，滑动变阻器的取值范围为11Ω-20Ω.

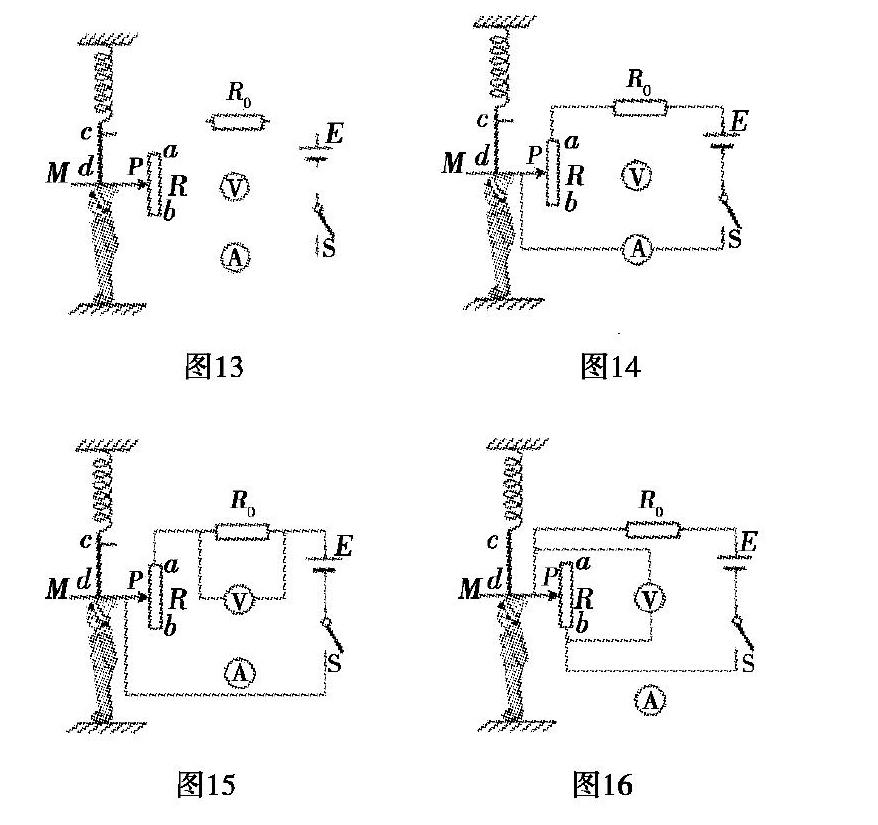
变式10：如图13所示，R0为定值电阻，R为滑动变阻器，金屬杆cd和MP（右端P是滑片）与电路接触良好，请设计测量人体身高的电路图.要求：人越高，电表显示的读数越大.

解析：测量人体身高的电路图的要求是“人越高，电表显示的读数越大”.由于滑动变阻器可以接上端，也可接下端，电表可以用电流表，也可以用电压表.所以，可以根据模型一，人越高，电阻越小，电流应越大，电压也应越大，可设计如图14、图15所示的电路图;也可以根据模型二，人越高，电阻越大，电流越小，电压却要越大，设计如图16所示的电路图.

3 结语

笔者在教学中紧扣两类基本模型，不断带领学生展开变式练习、拓展提升，能有效解决电表示数变化、电路故障、误差分析、动态电路和安全电路的计算、设计电路等系列难题，以不变应万变，渐近中进阶，有效地降低电学教学难点，帮助学生深化理解电学内容.

参考文献：

[1]吉临荣.解决物理动态问题的策略[J].理科考试研究，2020，27（10）：37-39.

[2]马兴卫.建构电路模型 解中考电学试题[J].中学物理，2011，29（10）：33-35.

[3]张睿，李静，季卫新.基于ARCS学习动机模型的区域初中物理深度备课教学实践——以初三电学复习课为例[J].物理教学，2020，42（03）：38-41.

[4]范胜邦.用数学模型巧解初中物理电学中的极值问题[J].数理化解题研究，2017（08）：72-73.

[5]梁艳.浅析初中物理电学的实验教学[J].吉林教育，2010（25）：95.

（收稿日期：2020-12-06）