改进MCKD 方法及轴承早期故障诊断研究

刘尚坤，王家忠，王泽河，弋景刚

（河北农业大学机电工程学院，河北 保定 071001）

1 引言

滚动轴承在水产品加工设备、风电机组、水泵等旋转机械中应用普遍，也容易产生磨损、点蚀等故障[1]。为保障设备准确、可靠、安全的运行，探索准确、快速的轴承故障诊断方法已成为学者们的研究热点之一[2]。

传感器获得的信号是轴承故障冲击成分与机械系统传递路径卷积的结果，而采用技术方法恢复故障冲击的过程就是解卷积的过程。最小熵解卷积（MED）采用迭代的方式达到峭度最大化目的，能够突出信号中脉冲成分[3]，但MED 解卷积效果只能突出少数尖脉冲且容易陷入局部最优中[4]。为了克服MED 的缺陷，文献[5]以相关峭度为准则提出了最大相关峭度解卷积（MCKD）算法，注重检测冲击成分的周期性，这与旋转机械故障时产生的周期性脉冲信息非常吻合，文献[6]利用MCKD 对信号进行降噪，再通过分析集合经验模态分解得到的高相关性分量实现了轴承故障的诊断，文献[7]将MCKD与重分配小波尺度谱结合诊断了空分机齿轮故障和轴承复合故障，但都没有细致研究滤波器的阶数选择问题。为提高MCKD 解卷积效果及应用的自适应性、避免其滤波器阶数选择的盲目性或受人为因素的干扰，以故障特征能量比最大化为寻优目标，提出变步长的搜索选择方式，并结合希尔伯特包络解调良好的解调能力[8]，实现轴承故障特征频率的提取和故障诊断。

2 改进MCKD 的轴承故障诊断方法

2.1 MCKD 算法

MCKD 采用相关峭度检测信号中冲击成分的连续周期性，将相关峭度最大作为目标函数，如式（1）所示。

该算法流程为：

（1）设置滤波器阶数L 等参数；

（2）计算待分析信号的X0XT0以及XmT；

（3）求出滤波后的输出结果y（n）；

（4）由y（n）计算αm、β；

（5）更新当前滤波器系数f；

（6）若滤波前后ΔCKM（T）＜ε，则迭代结束，否则转至（3）循环。

2.2 改进MCKD 的轴承故障诊断方法

为寻找最优的滤波器阶数，目标函数采用故障特征能量比η，η 由式（4）计算，表示包络谱中故障频率能量占全频段能量的比例[9]，比例值越大表明故障特征频率幅值越相对突出，说明滤波效果越佳。

式中：Xi—包络谱中故障特征频率第i 倍频处的幅值（取K=4）；

Xj—包络谱中全部序列。

以变步长寻优方式改进MCKD 的轴承故障诊断流程如下：

（1）针对待分析信号，设置滤波器阶数L 的寻优范围为［Lmin，Lmax］，设定大步长S1进行全局峰值位置寻优，获得目标函数η 最大时对应的峰值位置L1，再以L1为中心向前和向后分别扩展一个大步长设置新寻优范围［L1-S1，L1+S1］，重新设定小步长S2进行再次寻优，最终获得滤波器阶数的最优值L2。

（2）以L2为滤波器阶数利用MCKD 对原信号进行滤波处理，以达到提高信噪比、突显故障冲击成分的最好效果；

（3）求取滤波信号的希尔伯特包络谱，分析其中的故障特征频率，诊断故障类型。

值得注意的是波器阶数越大则MCKD 算法计算用时越长，在分析不同信号时可根据需要设定不同的［Lmin，Lmax］、S1、S2值。设定滤波器寻优范围［2，500］、大步长S1=10、小步长S2=1。

3 轴承数据分析

采用美国辛辛那提大学轴承全寿命实验数据[10]，实验台，如图1 所示。实验总用时164h，最后检查发现1 号轴承发生外圈磨损故障，采样频率fs=20kHz，外圈故障频率为236.4Hz。取第5300min 时的10000 个采样点加以分析，其时域波形和包络谱，如图2 所示。从时域波形中难以发现故障，包络谱中也没有出现突出的故障频率成分，表明故障处于早期。

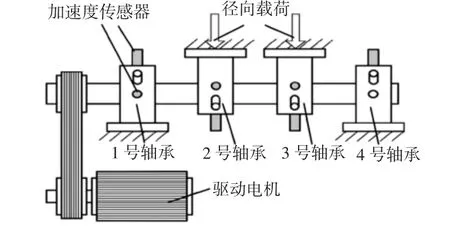
图1 全寿命轴承实验台Fig.1 Life-Cycle Bearing Test Bench

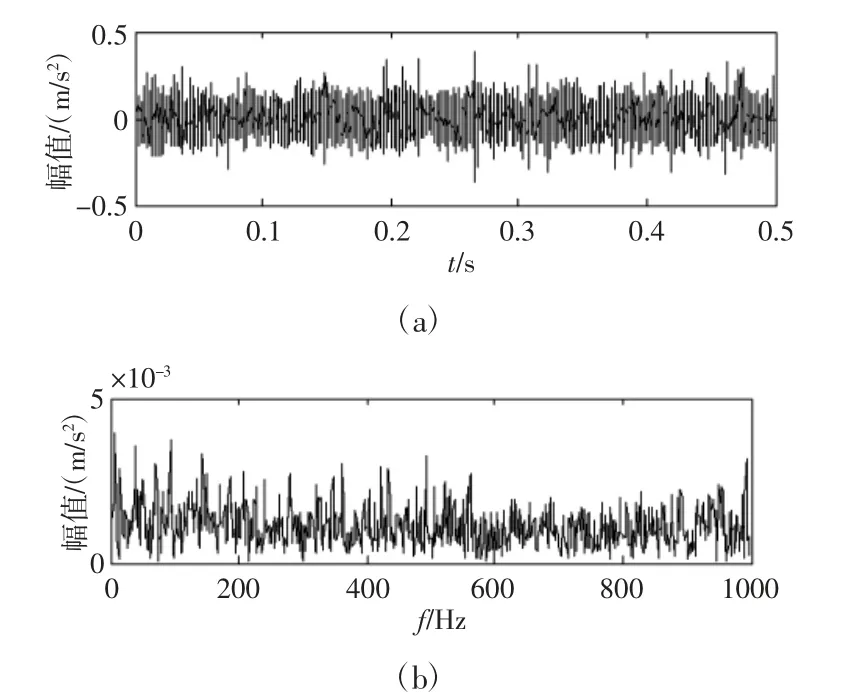
图2 外圈故障信号时域波形与包络谱Fig.2 Waveform and Envelope Spectrum of Outer Fault

利用改进MCKD 方法分析，先设定大步长S1=10，并在［2，500］范围内寻优滤波器阶数，特征能量比η 变化曲线，如图3所示。可知当L1＝92 时，η 最大值为0.0823；然后以L1为中心点，设置新的寻优范围［82，102］，并用小步长S2=1 进一步寻优，η 变化曲线如图所示，可见当滤波器阶数L2=89 时取得最优值，此时η 为0.0841。所以设定MCKD 的最优滤波器阶数为89 对原信号进行降噪滤波，得出MCKD 解卷积信号的时域波形和包络谱，时域波形的冲击幅值得到周期性增强，而包络谱则能够清晰的表示出外圈故障特征频率和二倍频，几乎没有干扰频率成分，因此可以准确诊断该轴承发生了早期外圈故障，如图4 所示。

图3 外圈故障特征能量比变化曲线Fig.3 Characteristic Energy Ratio Curve of Outer Fault

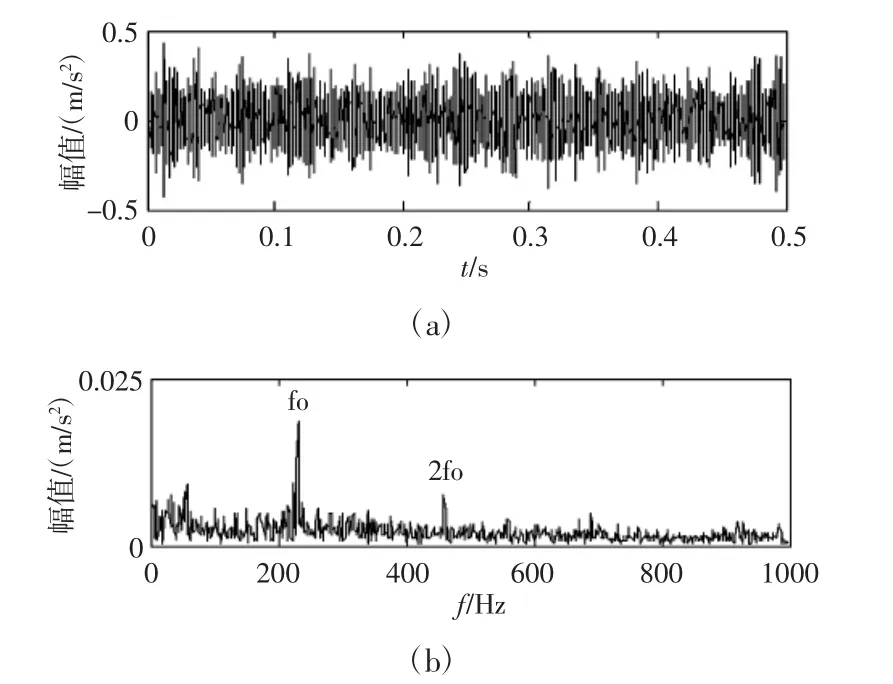
图4 改进滤波信号的时域波形与包络谱Fig.4 Waveform and Envelope Spectrum of Improved MCKD Filtered Signal

故障轴承振动信号的均方根值变化曲线，如图5 所示。分析可知该故障监测方式相对晚1720min 识别故障，说明改进MCKD方法在监测轴承早期故障时的有效性和优越性。

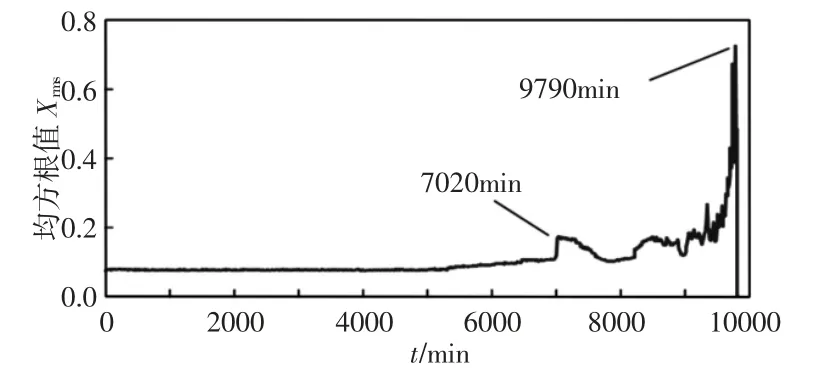
图5 轴承1 信号均方根值曲线Fig.5 RMS Curve of Bearing 1 Signal

为了与MED 方法对比，将该故障信号用MED 进行滤波处理，其时域波形和包络谱，如图6 所示。包络谱中虽然有故障频率成分，但干扰频率较多，不能准确诊断故障，相比这里方法效果差。

图6 MED 方法滤波信号的时域波形与包络谱Fig.6 Waveform and Envelope Spectrum of MED Filtered Signal

4 结论

MCKD 方法用相关峭度作为解卷积效果评价原则，能够检测和增强信号中的周期性冲击成分，但效果受到滤波器长度的影响。为了避免选择的盲目性，也为了高效、准确的选取滤波器阶数，以故障特征能量比为目标函数，采用变步长搜索方式，寻优MCKD 的滤波器阶数，实测轴承外圈故障分析结果均表明了方法的有效性，对比分析表明效果优于均方根值法和MED 方法，该方法可用作技术参考准确确诊轴承早期故障。