一个条件不等式的多种证明

石焕南,郑小彬,王东生

(1.北京联合大学 师范学院,北京 100011;2.福建泉州桃李教育咨询有限责任公司,福建 泉州 362000;3.北京电子科技职业学院 基础部,北京 100176)

1 预备知识

定理已知x,y为正实数,n为正整数,若x2n+1+y2n+1≥2,则

这个由意大利学者Francesco Cavazzan提出的不等式,虽然形式简洁,但证明起来并不轻松.本文利用受控理论[1]和分析方法给出四种不同的证明.

为此给出必要的定义与引理.设 ℝn,ℝn+和 ℝn++分别表示n维实数集,n维非负实数集和n维正实数集,并记ℝ1=ℝ,ℝ1+=ℝ+和 ℝ1++=ℝ++.对于x=(x1,x2,…,xn) ∈ℝn,将x的分量排成递减的次序后,记作x［1］≥x［2］≥…≥x［n］.

定义1[2,3]设x=(x1,x2,…,xn)和y=(y1,y2,…,yn) ∈ℝn.若

且

则称x被y所控制,记作x≺y.

定义2[2,3]设 Ω⊂ℝn,若在Ω上,

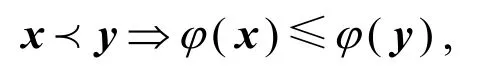
则称φ为Ω上的Schur凸函数,简称为S-凸函数;若-φ是Ω上的S-凸函数,则称φ为Ω上的S-凹函数.

杨镇杭[4]定义了Schur-f凸函数及Schur-幂凸函数,并研究它们的性质及判定.

定义3[4](a) 设f:ℝ++→ℝ是严格单调函数,Ω⊂ℝn,n≥2.若对于任何x,y∈Ω,总有

则称Ω是f-凸集,其中α∈ [0,1]且α+β=1;

(b) 设 Ω⊂ℝn,其内部非空.φ:Ω→ℝ+,对于任意x,y∈Ω,若

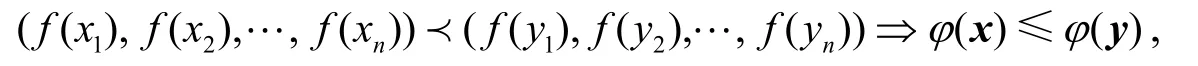
则称φ为Ω上的S-f凸函数;若φ-是Ω上的S-f凸函数,则称φ为Ω上的S-f凹函数.

定义4在定义3中,若取

则称φ为Ω上的m阶S-幂凸函数;若φ-是Ω上的m阶S-幂凸函数,则称φ为Ω上的m阶S-幂凹函数.

注在定义4中取f(x)=x可得S-凸函数的定义.

引理1[4]设Ω⊂ℝ是带有非空内部Ω°的对称集,φ:Ω→ℝ在Ω上连续且在Ω°上可微,则φ在Ω上Schur m-幂凸(Schur m-幂凹),当且仅当φ在Ω上对称且∀x∈Ω°(x1≠x2),有

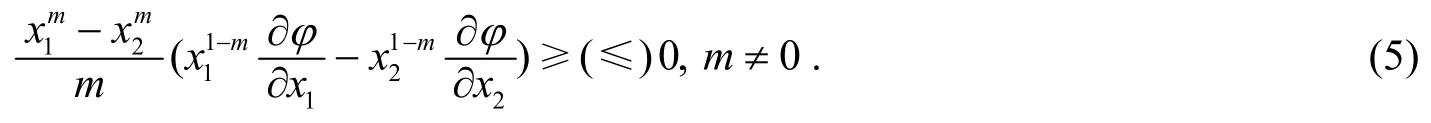
对于m≠0,因

即

若φ在Ω上Schur m-幂凸(Schur m-幂凹),则

定义5设(r,s)∈ℝ2,(x,y) ∈,定义二元Gini平均为:

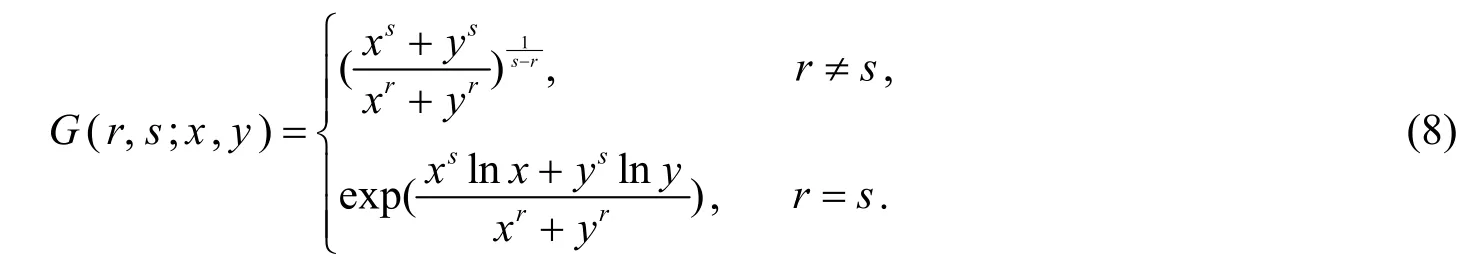
引理2[5]对于固定的(x,y)∈ℝ2+且x≠y,G(r,s;x,y)在 ℝ2+上关于(r,s)Schur-凹,在 ℝ2-上关于(r,s)Schur-凸.

引理3(Gini平均比较定理)[6]设x,y∈ ℝ++,p,q,r,s∈ℝ,(p-q)(r-s)≠0,则

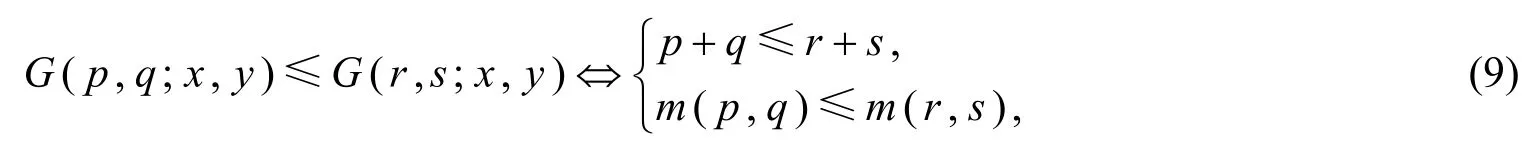
其中

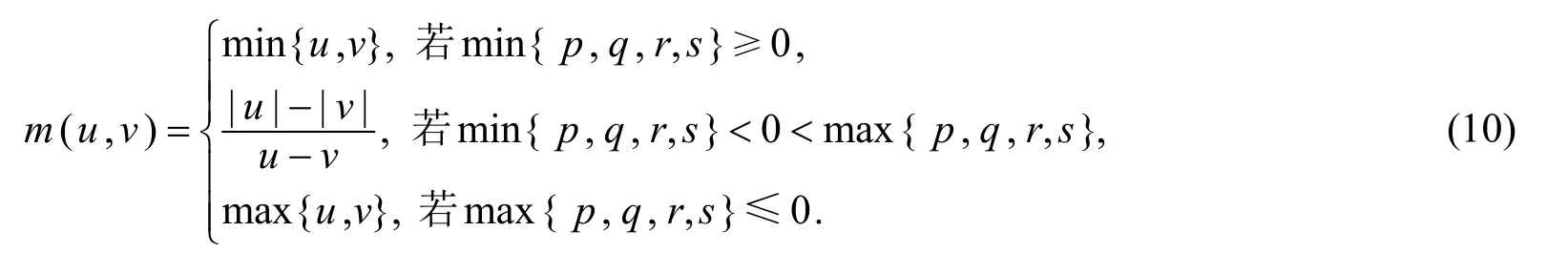
2 定理的证明

证法1令

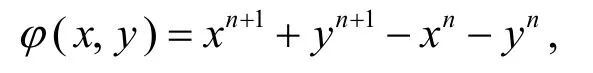
分两步证明.

(I) 若x2n+1+y2n+1=2,此时,由幂平均的单调性,有

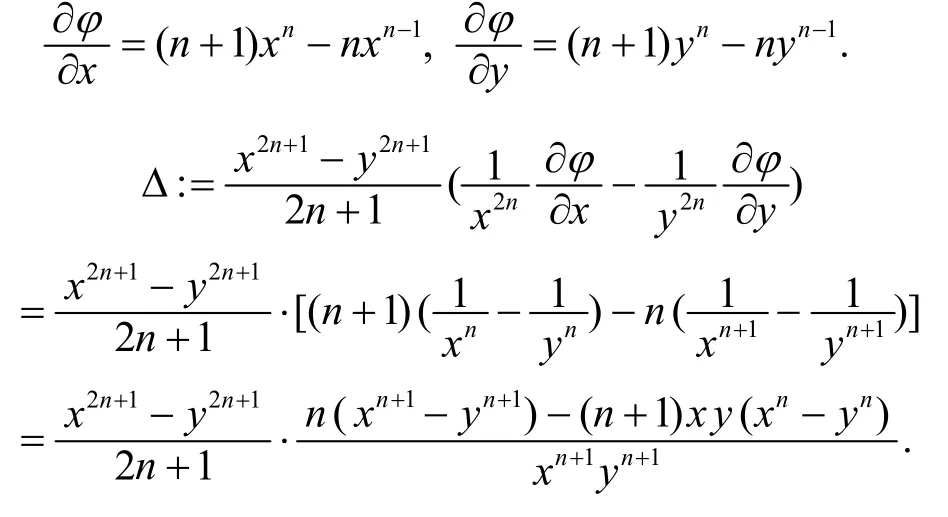
欲证Δ≥0,只需证n(xn+1-yn+1)≥(n+1)xy(xn-yn),即

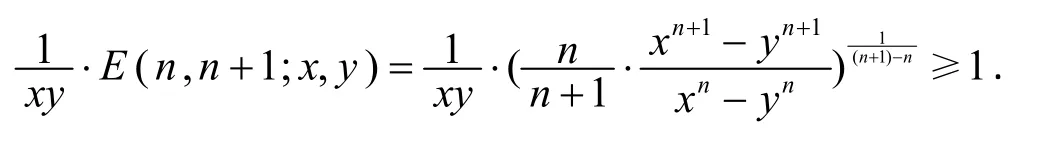
由文[1]定理1.1知,E(n,n+1;x,y)在上Schur-凸,故

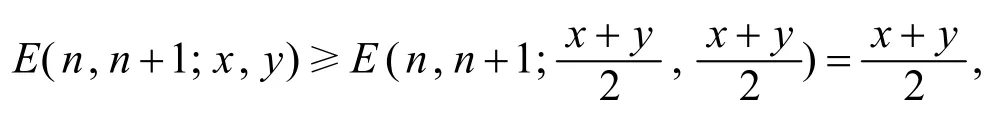
从而

故Δ≥0,由引理1,φ是上的2m+1阶S-幂凸函数,从而

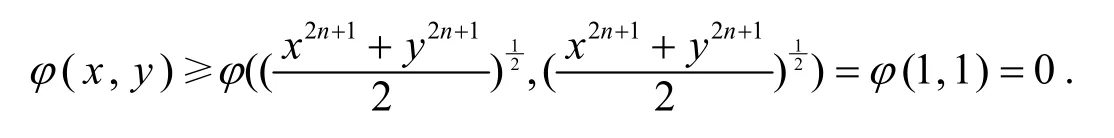
(II) 若x2n+1+y2n+1=a＞2,则

由(I)有

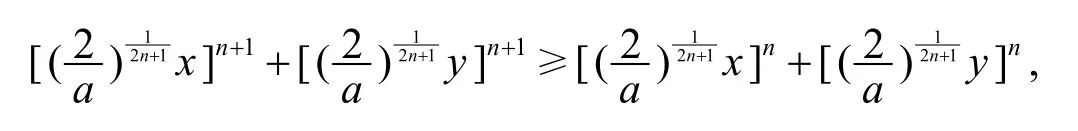
即

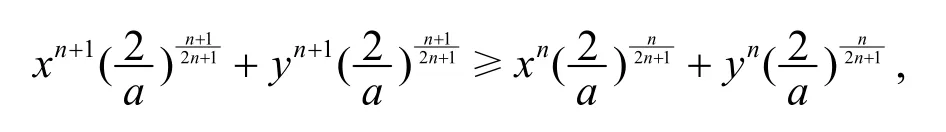
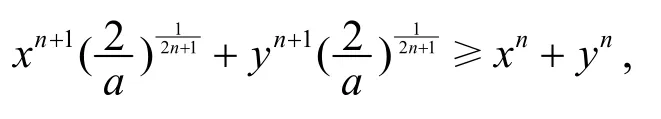
证法2据引理2,G(r,s;x,y)在 ℝ2+上关于(r,s)Schur-凹,由(n+1,n)≺(2n+1,0),有

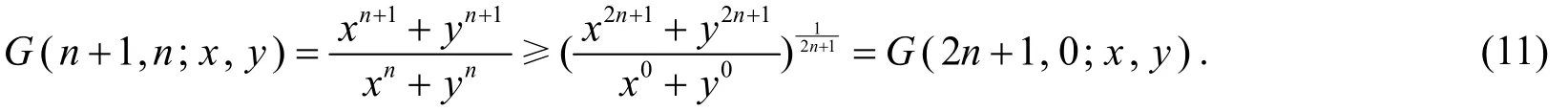
结合条件x2n+1+y2n+1≥2即得证.

证法3所证不等式等价于

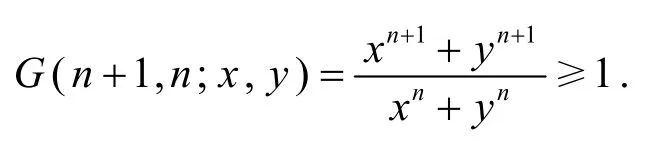
由条件x2n+1+y2n+1≥2,只需证

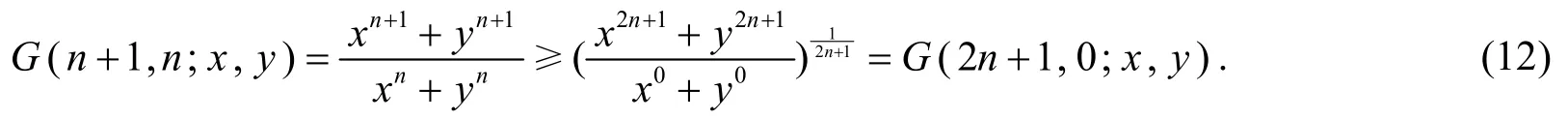
因n+1+n=2n+1+0,且min{n+1,n}=n＞min{2n+1,0}=0,由引理3知不等式(12)成立.

证法4不妨设x≥y,令x=ty,则t≥1.于是条件x2n+1+y2n+1≥2化为

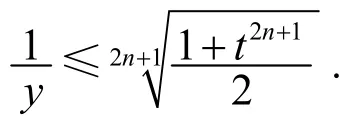
因xn+1+yn+1≥xn+yn等价于只需证

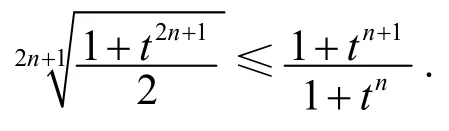
令

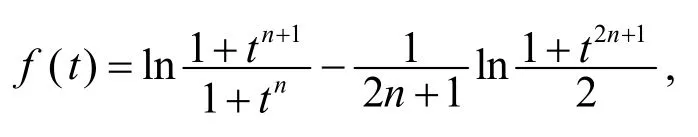
则

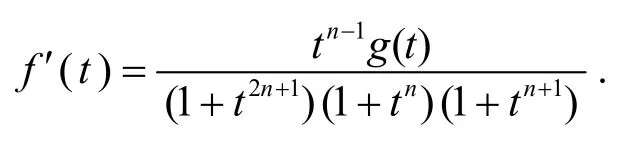
其中

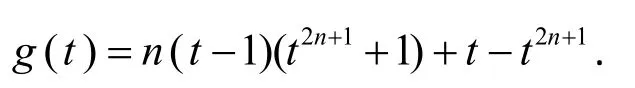
因

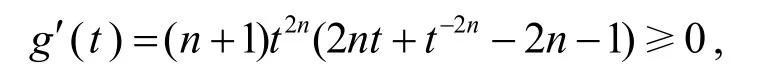
g(t)≥g(1)=0,故f′(t)≥0,进而f(t)≥f(1)=0,由此得证.