零点到两个闭半代数集的Minkowski和上的投影问题的数值算法

蒋 琼,周光明

(湘潭大学 数学与计算科学学院,湖南 湘潭 411105)

0 引言

Minkowski和是计算几何的一个重要概念,在理论和实际应用中都有重要的作用,常用于机器学习、路径规划、动态仿真等领域.

Han[1]等提出一种计算平面几何模型的Minkowski和的有效算法;张剑飞,郭希娟[2]针对非凸多面体的Minkowski和计算过程中剖分和合并复杂度过高的问题,提出一种基于阈值剖分的非凸多面体的Minkowski和计算方法;马绍惠[3]等采用凹多面体回路的近似精确算法设计对求Minkowski和的边界值的算法进行改进;郭希娟[4]等提出一种基于边平移理论的二维平面内两凸多边形的Minkowski和构造算法,并分析验证了所提算法的性能;Yan[5]给出n维欧几里得空间中两个任意取向实心椭球的Minkowski和的和差边界的显式闭型参数化公式;Mizrahi[6]等提出一种计算两个自由曲面Minkowski和的方法;Higashitani[7]研究了整凸多边形Minkowski 和的正态性或整数分解性质;Zhao[8]设计了一种新的三维凸包计算方法,通过空间两凸多面体外表的点云信息直接计算其Minkowski和,用计算得到的凸包的面集表示Minkowski和的边界信息;Bauschke[9]等提供了一个完整的答案来表明闭凸集Minkowski和上的投影等于单个投影的和;Gabidullina[10]对欧氏空间原点在凸多面体上的投影问题进行了研究,系统地给出了不同公式;Qin[11]等研究了从一点到一般凸集的Minkowski和的投影的计算问题以及最小距离的计算问题.

本文针对两个闭半代数集的 Minkowski和,提出计算零点到该和上的投影的数值算法.这里不要求闭半代数集是凸的.进一步分析了算法的收敛性,并通过数值实验验证了算法的有效性.

1 预备知识

Ω1,Ω2是 ℝn的两个子集,集合 Ω1,Ω2的Minkowski和的定义为:

下面给出相关符号、定义和定理等[12].

设α=(α11,…,α1n,α21,…,α2n)T∈ ℕ2n,x:=(x1,x2)=(x11,…,x1n,x21,…,x2n)T∈ℝ2n,记

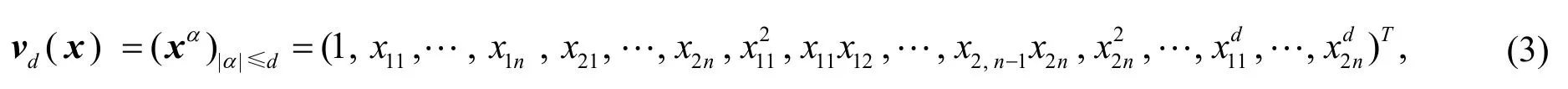
其中所有的单项式xα的次数都小于等于d,以上向量称为次数不超过d的多项式集ℝ[x]d的标准基,其维数为

定理1[12](Riesz-Haviland) 令且 Ω⊂ℝ2n是闭集.在Ω上存在一个有限的Borel测度μ使得

成立,当且仅当Ly(f)≥0对任意在Ω上的正多项式f∈ℝ[x]都成立.

下面是矩矩阵与局部矩矩阵的定义.

给定s(2r)维的序列则矩矩阵Mr(y)的维数为s(r),其元素为

等价地有Mr(y)=Ly(vr(x)vr(x)T)成立.

设多项式u(x) ∈ℝ[x],其系数向量为u={uγ},局部矩矩阵Mr(u(x)y)的元素为

等价地有Mr(u(x)y)=Ly(u(x)vr(x)vr(x)T)成立.

本文主要讨论的零点到两个闭半代数集的Minkowski和上投影问题为如下最小范数问题:

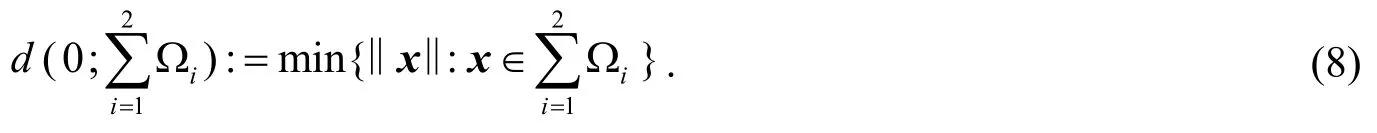
其中

是 ℝn上的闭的基本半代数集,gij(xi) ∈ℝ[x]且gij(xi)的次数为2vij或2vij-1.

由式(1)、(8)和(9)可知,我们需要求解的是如下等价的多项式优化问题:

根据Lasserre半正定松弛方法[12],将多项式优化问题(10)转化为半正定规划问题:

其中s≥s0:=maxi=1,2,j=1,2,…,qivij.

以上半正定规划问题(11)在约束集合为紧的情况下其对偶也是一个半正定规划问题,有如下形式:

综上可知,所求最小范数问题是一个多项式优化问题,可以利用Lasserre提出的半正定松弛方法进行求解,具体算法如下:

输入:目标函数f(xi)和约束条件gij(xi)≥0,i=1,2,j=1,2,…,qi以及最高松弛次数k.

输出:最优值f*和一列全局最小解,i=1,2,l=1,2,…,n或f*的下界ρk.

Step 1 求解半正定优化问题的最优值ρs和最优解x*(如果存在的话).

Step 2 若没有最优解x*,则ρk只作为一个满足ρk≤f*的下界.若s＜k,则令s:=s+1,返回Step 1进行计算;若s≥k,则终止运算并输出ρk.

Step 3 若 rankMs-s0(x*)=rankMs(x*),则ρs=f*且至少存在 rankMs(x*)个全局最小值点.

Step 4 若 rankMs-s0(x*)≠rankMs(x*)且s＜k,则令s:=s+1,返回Step 1进行计算;若s≥k,则终止运算并输出满足条件ρk≤f*的ρk.

2 收敛性分析

其中i=1,2,j=1,2,…,qi.

假设1存在u(x)=u(x1,x2) ∈Q(g)使得水平集 {x∈ℝ2n:u(x)≥0}是紧集.

前述算法的收敛性定理为:

定理2令假设1成立且半正定松弛问题(11)有最优解ρs,则

(a)ρs↑f*(s→∞),

证明因为(10)是一个多项式优化问题,所以根据假设1以及相关定理[12]直接可得结论成立.

3 数值实验

下面通过数值实验来检验上述算法的有效性.所有数值结果均通过 MATLAB 2016b 计算得到.实验电脑配置如下:双核2.20 GHz CPU,运行内存为4GB.MATLAB 通过调用SeDuMi[14]和GloptiPoly[15,16]来求解转化后的多项式优化问题.

表1和表2中L-SDP行表示由 Lasserre 半正定松弛方法求得的结果;fmincon行表示由MATLAB 中的函数fmincon求得的结果.其中x0表示初始点;x*表示最优解;f*表示最优值;‘’/’’ 表示不需初始点.

算例1令

这里Ω1与Ω2都是非凸的,零点到的投影问题为:

算例1的数值结果见表1.

表1 算例1的数值结果

由表1可以看出,Lasserre 半正定松弛方法求得的最优值与fmincon函数在以初始点为(3,2,7,7)时计算得到的最优值几乎一致,比用fmincon函数计算的另两个初始点的结果更好.

算例2令

这里1Ω与Ω2都是非凸的,零点到的投影问题为:

算例2的数值结果见表2.

表2 算例2的数值结果

由表2可以看出,Lasserre 半正定松弛方法求得的最优值与fmincon函数在以初始点为时计算得到的最优值几乎一致,比用fmincon函数计算的另两个初始点的结果更好.

以上数值结果表明Lasserre半正定松弛方式是有效的，且具有不依赖初始点的优点.

4 总结

本文主要讨论了零点到两个闭半代数集的Minkowski和上的投影问题,通过将问题转化为多项式优化问题,提出用Lasserre半正定松弛方法对其进行求解的数值算法,该算法不要求闭半代数集是凸的,并进行了一系列数值实验,数值结果表明了算法的有效性.