基于稳健回归的颗粒物浓度预测研究

廖文辉,林 睿,何志锋,黄嘉莹

(1.广东金融学院,广东 广州 510520;2.江西财经大学,江西 南昌 330032)

0 引言

近年来,颗粒物污染(PM2.5)给城市居民的生活带来了许多负面影响,不仅影响了气象能见度,造成交通阻塞,还会对人的健康产生很大影响,例如呼吸系统疾病、心脑血管疾病、精神健康问题、肺癌和过早死亡等都与空气质量有直接或间接的关系.尤其像京津冀、长三角、珠三角以及四川盆地等城市群地区,经济发达,人口密集,也是空气污染最为严重的区域.控制PM2.5浓度因素可以分为污染物排放和气象要素两个方面[1],控制PM2.5浓度的过程包括了排放、传输、转换以及沉降[2～5].除排放之外,其余过程都受到天气条件影响[6],因此构建PM2.5浓度统计模型主要从这两个方面入手.Zhu[7]等将滞后一天和滞后两天的空气污染物与气象因素作为PM2.5浓度的影响因素,其中空气污染物包括PM10、一氧化碳(CO)、二氧化氮(NO2)、臭氧(O3)和二氧化硫(SO2);气象因素包括气压、温度、相对湿度、风速和日照时间等.柏玲[8]等研究表明,NO2、CO是影响PM2.5浓度的两项主要空气污染物,而降水量和相对湿度则是影响PM2.5浓度的两个重要气象因素.梅波[9]等研究表明,空气污染物CO、NO2、SO2对PM2.5浓度的直接影响为正,对O3的影响为负,气象因素中气温、气压、降雨量以及前一期的降雨均为负效应,而湿度为正效应.

线性回归是确定两种或两种以上变量间相互依赖定量关系的一种统计分析方法,应用范围十分广泛.当回归分析中包括两个或两个以上的因变量和自变量,且因变量和自变量之间是线性关系时,即为多元线性回归模型(Multivariate Linear Model,MLM).在MLM中,最常用的估计方法是最小二乘法(OLS)估计.现实中的PM2.5浓度数据有很多异常值,比如:监控过程中机器发生故障、周围环境的异常改变等都会引起异常值的出现,而最小二乘法得到的参数估计非常容易受到异常值影响,从而影响PM2.5浓度的预测准确性.稳健回归是统计学稳健估计中的一种方法,其主要思路是将对异常值十分敏感的经典最小二乘回归中的目标函数进行修改,将稳健方法应用于回归模型,以拟合大部分数据存在的结构,同时可识别出潜在可能的离群点、强影响点或与模型假设相偏离的结构.当误差服从正态分布时,其估计几乎和最小二乘估计一样好,而不满足最小二乘估计条件时,其结果优于最小二乘估计.

本文引入常用稳健回归中的S估计、M估计、MM估计、MCD估计和传统的OLS估计建立模型,对PM2.5浓度进行预测并比较其效果,为设计空气污染统计预测模型提供选择和参考.

1 MLM稳健估计

1.1 MLM模型介绍

设有p个自变量x1,x2,…,xp,q个因变量y1,y2,…,yq的n次观测样本(x1t,x2t,…,xpt,y1t,y2t,…,yqt)t=1,2,…,n.矩阵表达式为:

于是多元线性回归模型可表示为:

其中B为q×p维系数矩阵,β0为q维截距向量,e(t)为残差项.

其分量e(t)之间相互独立,t=1,2,…,n,每个e(t)的均值向量为0,协方差矩阵为∑e.假设(X,Y)服从联合正态分布,μ表示(X,Y)的联合分布的期望向量,∑表示(X,Y)的联合分布的协方差矩阵.显然,可以利用样本估计多元正态总体参数μ和∑,再通过分块矩阵获得线性模型(3)的参数β0和B的估计.

1.2 M估计

M估计(Maximum Likelihood Type Estimates,M-Estimator)由Huber[10]于1964年提出,也称作广义最大似然估计,是最常用的稳健估计方法.许多其它稳健估计方法都是在M估计的基础上发展起来的.

M估计应用在回归方程中,准则如下:

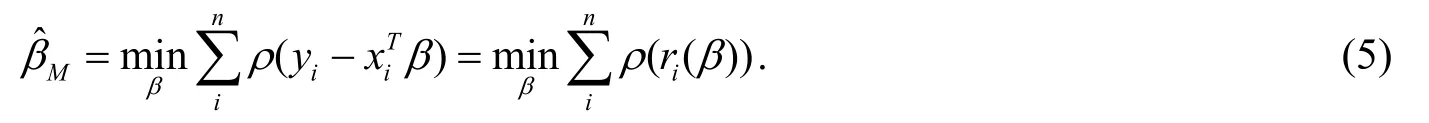
其中ri(t)是残差项,ρ(t)为目标函数,也称为残差损失函数,满足下述假设条件:

(ⅰ)ρ(t)是光滑正值实函数;

(ⅱ)t≥0时,ρ(t)单调不减;

(ⅲ)ρ(0)=0,maxρ(t)=1.

1.3 S估计

S估计追求样本马氏距离的某M-尺度统计量最小,也是单变量尺度参数M估计的推广,故称为最小化残差尺度S估计[11].对于样本数为n的集合,记各样本马氏距离为目标函数为ρ(t),也称为残差损失函数,这里取光滑且极限为1的正值函数.通过求解得为样本M-尺度统计量,这里δ取0.5.显然样本马氏距离与参数估计量有关,则多元总体参数的S估计定义为

S估计通常没有显性表达式,一般通过数值方法近似求解,需要一个稳健且方便计算但效率一般的估计量作为迭代的初始值.

1.4 MM估计

S估计存在低维情况下估计效率不高的问题,这主要是因为卡方分布在p较小时非对称所致.MM估计则能有效提高低维情况下的估计效率,其计算过程如下:首先寻找一个有偏高稳健的初始估计,求初始的样本马氏距离与S估计类似,定义样本M-尺度统计量对于每一个集合定义估计量为使得成立的解,那么MM估计为满足的解,其中c用于调整有效性[12,13].

1.5 MCD估计

MCD估计,也称最小化协差阵行列式估计,由Rousseeuw[14]提出.常用样本协差阵行列式最小的h个样品构造的子集估计均值向量和协差阵.考虑一个n行p列的矩阵Xn×p,从中随机抽取p+1个样本组成子集J,分别计算T0=ave(J),S0=cov(J),如果S0的行列式 det(S0)=0,则子集J随机增加一个数据再计算S0,直至 det(S0)≠0;计算n个样本数据到初始中心T0的马氏距离选出这n个距离中最小的h个;然后再通过这h个样本计算样本均值T1和协方差矩阵S1,如此迭代称C-步迭代,可以证明 det(Si)≤det(Si+1),直到当 det(Sm)≈det(Sm-1)时停止迭代,这时再通过Sm进行加权计算,求出稳健的协方差矩阵估计量.h值选择确保稳健方法有最高崩溃点.Rousseeuw[15]还提出一种快速MCD估计算法,目前在各统计软件包中均有使用.

2 实验分析

根据世界卫生组织数据显示,每年因空气污染造成的死亡人数达700万.因此,如果能开发优秀的统计模型对空气污染进行预测掌控,就可以降低或避免其对居民生活的影响[16].空气污染主要受气象条件和污染排放的影响,而这两方面的实时监控都存在不少困难,特别是污染排放.本文以广州万顷沙环境监测站2014年9月至2016年12月的空气污染物浓度数据为例(数据来源:粤港澳空气质量监测网络),引入常用稳健方法中的S估计、M估计、MM估计、MCD估计和传统的OLS估计建立回归模型,对PM2.5浓度进行预测,比较其效果的差别.

2.1 变量选择

所用数据集的样本容量n=852;自变量个数p=12(包括六个气象指标:风速(Spd)、位势高度(Hgt)、温度(Temp)、露点温度(Dewpt)、海平面气压(Slp)、相对湿度(RH);六个滞后一天的污染物浓度:二氧化硫(Pre_SO2)、二氧化氮(Pre_NO2)、一氧化碳(Pre_CO)、臭氧(Pre_O3)、颗粒物2.5 mm(Pre_PM2.5)、颗粒物10 mm(Pre_PM10));目标变量为当前的颗粒物2.5 mm(PM2.5)浓度.目前,气象预报有比较成熟的体系,可以较准确地预测未来三天的气象条件.因此,基于当前气象条件和历史污染物浓度作为自变量来构建MLM预测当前空气污染物浓度是稳妥做法.根据广义可加模型(GAM)分别对12个解释变量进行筛选.首先建立单因素的GAM模型,选择Identity连接函数,使用样条平滑函数进行拟合,根据得出的方差解释率进行初步的变量筛选.结果见表1.从计算的结果分析可得,所有变量的方差解释度都超过了10%,因此都可以选进回归方程.

表1 PM2.5浓度单因素GAM模型拟合结果

2.2 稳健回归模型构建与预测

为了选择更好的稳健估计方法,进行100次随机模拟,每次从样本中抽取30%样品作为测试集,其余样品作为训练集.采用均方预测误差根(mean squared prediction error roots)

自变量包括当天的气象指标和前一天的污染指标共12个指标,因变量为PM2.5.比较方法包括S估计、M估计、MM估计、MCD估计和传统的OLS估计.为增加结果的参考价值,在样本中加入一定比例的异常值作比较研究,异常值比例a取0,0.1,0.2和0.4这四种情况,从均值和标准差都为100的正态分布中取值.比较结果见表2.

表2 不同污染下各方法的MSPER和Pcor

从表2可以看出,在实证数据集中没有污染的情况下,S估计、M估计、MM估计和MCD估计的预测结果都很理想,与传统最小二乘法较接近.当数据出现异常值时,传统方法OLS估计的预测效率马上下降,测试集的预测误差明显变大,预测值相关系数变小.而稳健方法的预测效果具有较好的稳定性,MCD估计在各种污染比例下的预测效率均最优,尤其在污染比例小于0.4时,随着污染比例上升,MCD估计预测效率超过了S估计、M估计、MM估计.考虑到污染比例不能超过0.5,上述结果表明MCD估计在各种污染比例上均有较好的预测效率.

3 结束语

本文采用多种稳健估计方法,对空气污染物浓度进行预测,并比较了这些方法的预测效率.对空气污染物浓度预报的实证分析结果表明,在不同污染率的情况下,稳健方法的预测效果具有较好的稳定性,其中MCD估计在各种污染比例下的预测效率均为最优,能更有效地消除或减弱离群点对回归系数估值的影响,具有更强的稳健性,且当污染率愈大时,这种效果愈明显.本文实证结果可以为开发空气污染统计预测模型提供更多的选择和思路.