基于神经网络算法的大跨径斜拉桥随机地震效应主梁动力可靠度研究
王思伟, 陈双庆, 雷顺成, 王祺顺
(1.湖南中大设计院有限公司,湖南 长沙 410014; 2.湖南文理学院 土木建筑工程学院, 湖南 常德 415000; 3.湖南省交通科学研究院有限公司, 湖南 长沙 410015)
随着桥梁结构计算理论的日臻完善和进步,结构安全控制研究方向正向着大跨径桥梁运营期结构可靠度领域转变,国内外众多学者对桥梁运营期受风荷载、地震荷载等随机荷载效应下结构力征及可靠度开展了大量的研究工作,取得了一定成果。但目前传统的桥梁动力可靠度分析仅能考虑地震激励本身的随机性,忽略了结构设计参数的随机性对桥梁地震可靠度的影响,具有一定的局限性,同时,目前主流的可靠度计算方法(如一次二阶矩法、蒙特卡洛法和响应面法)计算高次超静定结构可靠度时,需进行多次迭代,样本数据庞大,适用性不高[1]。基于此,本文以某大跨径斜拉桥为背景,基于首次超越准则,构建地震效应和结构设计参数双重随机性功能函数,提出使用神经网络算法对结构动力可靠度进行分析,相关成果可为大跨径斜拉桥在地震作用下的结构可靠度计算方法研究提供一定参考。
1 首次超越准则下动力可靠度功能函数构建
1.1 首次超越准则在动力可靠度中的应用
首次超越准则是对结构动力响应极值(控制截面动位移、内力等)首次跨越临界值的一种描述,可分为单侧界限、双侧界限和包络界限3种描述方式[2]。以单侧界限为例,基于首次超越准则的动力可靠度表达式见式(1)。
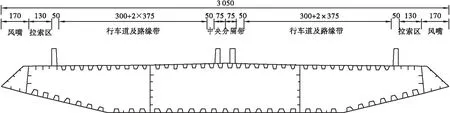
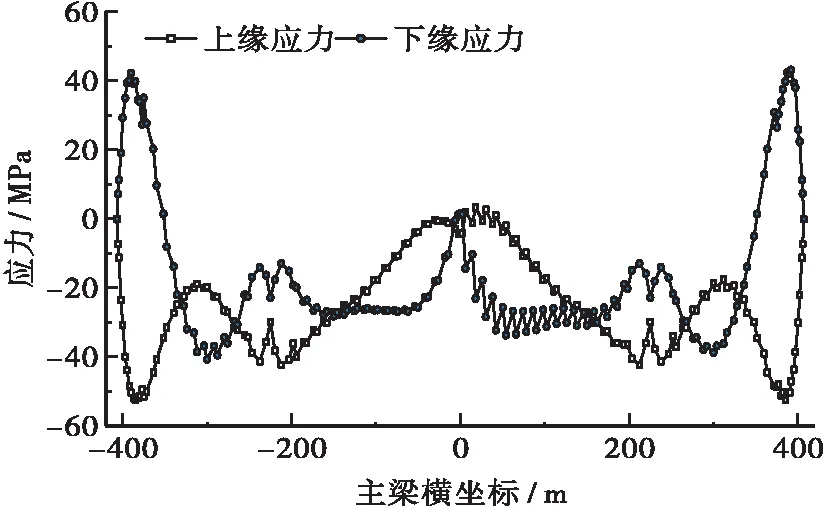
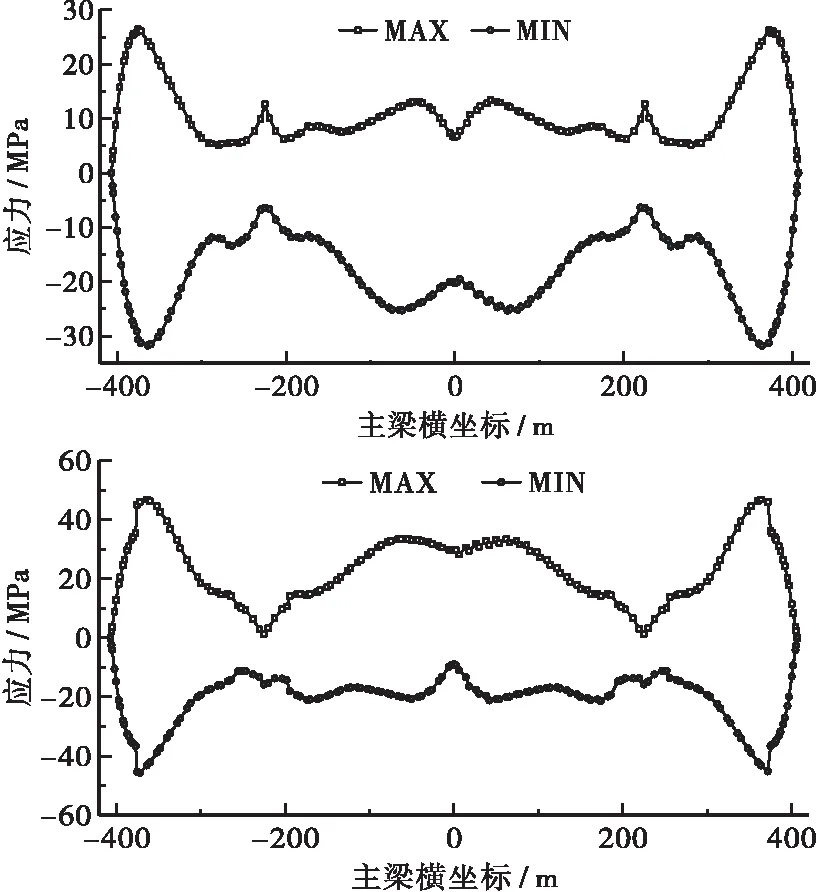
Pr(b)=P{max[x(t)]≤b,0 (1) 式中:P(x)表示事件发生概率;b为界限值;t为事件参数;T为事件持续时间;max[x(t)]为随机事件x(t)的响应极值。 在时间[0,T]内,设响应极值与临界界限x=b存在交点个数为nb(T),参数期望值为Nb(T),单位时间内期望值为Vb(T),交叉速率为Vb(t),考虑到Vb(t)是与时间无关的参数,则有: (2) 引入联合概率函数fx,x’(x,x’,t),联合式(2)可得: Nb(T)=Vb(t)= (3) (4) (5) 考虑高斯平稳随机过程,同时假定事件响应值x和界限值b交点次数呈现为稀有泊松分布形态,则结构在[0,T]时间内动力可靠度可描述为式(6)的形式。 (6) 基于首次超越准则,构建随机振动荷载下结构可靠度功能函数见式(7),其中,Z(t)表示随时间变化的功能函数,R表示结构临界值,一般通指结构抗力值,dmax表示在特定时间[0,T]内响应极大值,由式(7)即可求得结构在随机荷载激励下的最小可靠度。 Z(t)=R-dmax(t) (7) 在结构响应值计算时,结构内力响应极大值可表示为dmax=ρσd,其中ρ为随机变量参数值,σd表示结构内力响应均方根,其统计特征值见式(8)。 (8) 记结构本身参数随机性为X=(x1,x2,x3,…,xn),其中1~n分别表示结构参数变化量,如质量密度、弹性模量、阻尼比、泊松比等,考虑结构在恒载G和活载Q下结构力学响应值,则结构在随机振动激励和结构本身参数随机性耦合作用下的双重随机性动力可靠度可表述为式(9),联立式(8)、式(9)即可求解[3]。 Z(t)=R-G(X)-Q(X)-ρσd(X) (9) 目前,对于隐函数描述的可靠度表达式,无法通过一次二阶矩法直接求解。主流方法有蒙特卡洛抽样法和响应面法,蒙特卡洛抽样法通过抽样形成初始参数序列,通过求解式(9)中的结构内力响应值从而计算得到可靠度值,但为保证计算精度,抽样次数过多,样本庞大,不利于大型复杂结构的求解;响应面法计算精度依赖于功能函数的拟合程度,当结构为简单线性结构时,采用二次多项式即能达到精度要求,但对于高次超静定结构,简单的二次多项式难以满足要求,更高次的多项式拟合则容易导致求解困难,以上两种方法均不适用于大跨径高次超静定桥梁动力可靠度的计算[4-5]。 与传统响应面法相比,BP神经网络无需使用具体的函数对功能函数进行拟合,而是通过对样本数据进行学习和训练,建立对应的映射关系作为拟合条件。对于服从高斯分布的随机变量(x1,x2,x3,…,xn),在正态坐标系中,其可靠度指标的几何意义为原点到极限状态曲面的距离极小值,故通过求解其最短距离即可获取可靠度指标[6]。 (10) Matlab工具箱中的线性规划优化方法提供了较为便捷的极值求解模块,线性规划求解可有效规避对于映射关系梯度方向求解困难这一缺点,同时对于收敛性的要求也较低,是一种广泛应用的极值求解方法[7-8],具体步骤如下所示: a.在ANSYS中建立结构参数化有限元模型,输入合适的随机地震荷载,获取结构响应期望穿零率,并计算随机变量参数ρ均方根和方差。 b.在Matlab中生成结构本身参数随机变量样本数据(x1,x2,x3,…,xn),计算样本数据平均值ux,将其定为初始迭代序列样本中心点。 c.建立Matlab与ANSYS相互调用程序,在ANSYS有限元模型中获取随机地震荷载下结构内力响应均方根σd,以结果文件的形式输出至Matlab中。 d.对数据样本进行神经网络训练,建立对应映射关系,以数据样本均值ux和响应均方根σ’d作为输出和期望输出结果。 e.将通过net映射得到的均方根σ’d与有限元输出的σd对比,进行误差检验,若两者差值满足精度要求,则调取Matlab中线性规划优化工具箱,利用式(10)直接求解可靠度指标;若精度不满足要求,则选取新的样本点数据,重新进行神经网络训练,重复上述步骤,直至满足要求为止。 f.输出结构可靠度指标β,结构最小可靠度为ρmin=ψ(β)。 本文工程背景为湖南高速某特大跨钢箱梁斜拉桥。该桥桥跨布置为(182+450+182)m三跨两塔双索面钢箱梁斜拉桥,结构形式为半漂浮体系,设计荷载等级为公路—I级,桥梁全宽30.5 m,其中扁平钢箱梁宽27.1 m,两侧导风风嘴分别为1.4 m,整体采用Q345D钢材。整桥对称分为17个吊装焊接节段,桥面铺装为正交异性钢桥面板,斜拉索采用抗拉标准强度为1 770 MPa的高强预应力钢绞线,外置粘滞阻尼器,索间标准间距12 m,加密区5 m。桥址地震基本烈度为Ⅶ度,地震峰值加速度为0.05g,反应谱特征周期0.35 s。桥梁立面布置图及横截面示意图见图1、图2。 图2 标准钢箱梁节段横截面布置(单位:mm) 图1 桥梁立面布置(单位:cm) 图3为该斜拉桥参数化有限元模型示意图,整体采用鱼刺法建模。其中钢结构主梁采用Beam188梁单元模拟;斜拉索使用Link10三维杆单元模拟并设置为仅受拉特性,成桥索力以施加实常数的形式输入,同时根据Enrst公式对斜拉索弹性模量进行几何非线性修正,修正后结果以参数数组形式重新赋予至材料特性指标中;斜拉桥主塔使用Solid45实体单元建模,斜拉索与主塔扣点采用共节点约束,主梁与主塔之间建立弹簧单元,通过设置弹簧DY、DZ、RX3个方向的刚度实现对半漂浮体系的模拟。 图3 斜拉桥ANSYS有限元模型示意图 为较为精确地考虑地震波的随机性,本文拟采用虚拟激励法实现对地震加速度的模拟,在斜拉桥各支撑约束位置建立Mass21质量单元并施加109kN重力荷载。其目的为通过在结构约束支撑位置施加一质量无穷大的质量块,使得结构总质量绝大部分为支撑约束位置的质量,求解得到的支撑约束位置的加速度即可等效为实际地震荷载的加速度,该方式可解决ANSYS中难以模拟实际加速度的困难[9]。 斜拉桥属于柔性结构,振动频率小,低频成分复杂且相互干扰,容易给结构抗震分析带来困难。杜修力模型则能很好地解决结构低频振动时能量过大造成奇异点的问题,对于斜拉桥和悬索桥等柔性结构的地震频谱特性描述,具有良好的适应性。故本文选取杜修力模型作为随机地震功率谱输入模型[10]。具体表达式见式(11)。 (11) 式中:ωg、ξg为场地土卓越频率和阻尼比;D为加速度脉冲宽度;ω0为低频频率;s0为初始震源函数谱。 根据桥址地勘资料及杜修力模型参数输入方法,取以下参数作为输入参数:s0=17.26 cm2/s3;D=0.011 4;ω0=1.83;ωg=13.03;ξg=0.03;X、Y、Z方向加速度比值为1∶0.85∶0.65,功率谱密度比为1∶0.722 5∶0.422 5,将各参数输入至杜修力模型中,经二项式展开可得X、Y、Z功率谱密度值分别为:sox=17.26 cm2/s3;soy=14.671 cm2/s3;soz=11.219 cm2/s3,功率谱密度曲线图见图4。 图4 杜修力模型功率谱密度曲线图 根据上述理论,在ANSYS中通过虚拟激励法模拟地震随机效应,获取结构在随机地震荷载下的内力响应均方根结果,获取结构恒载、活载及杜修力模型描述的随机地震荷载3个工况下主梁内力响应均方根结果。 由图5~图7可知,斜拉桥主梁在杜修力模型下边跨约L/6截面(边跨支座位置)和跨中截面位置存在应力响应峰值;在恒载作用下边跨L/6截面、主塔与主梁相交截面以及跨中截面存在应力响应峰值;活载作用下边跨L/6截面出现应力响应峰值。故可认为边跨L/6截面、中跨跨中截面及塔梁相交截面3个位置为响应控制截面。 图5 随机地震荷载效应主梁上下缘应力均方根 图6 恒载效应主梁上下缘应力均方根 图7 活载作用下主梁上下缘应力均方根包络图(左为上缘) 由式(9)可知,恒载响应、活载响应及随机地震响应均为关于结构本身参数随机性的函数,选取主梁弹性模量、主梁质量密度、极限强度及结构阻尼比4个参数作为随机性变量,结构参数随机性分布特性见表1。获取结构参数随机性分布特征后,将其作为初始样本数据,根据第2节阐述的计算方法,在Matlab中编制程序,利用神经网络算法对样本数据进行训练,经迭代计算收敛后输出可靠度指标并计算结构可靠度,并将计算结果与传统响应面法计算结果进行对比,具体见表2。 表1 结构参数随机性统计表Table1 Statisticaltableofrandomnessofstructuralparameters弹性模量/MPa质量密度/(kg·m-3)极限强度/MPa阻尼比均值2.05e578003450.01变异系数0.150.20.10.2分布特征正态分布对数正态分布对数正态分布正态分布 表2给出了分别运用神经网络算法和传统响应面法斜拉桥控制位置截面动力可靠度结果对比,两种算法得到的结构最小动力可靠度均大于4.7,满足规范要求,说明该桥在地震作用下具有良好的可靠性。同时,两种方法下控制截面可靠度计算结果极为接近,最大相差仅为1.2%,但是神经网络算法迭代次数较传统响应面法更少,调用ANSYS有限元结果次数也更少,说明神经网络算法在保证计算精度的同时,具有更快的拟合速度,对于复杂非线性结构的动力可靠度分析,基于自适应学习的神经网络算法具有明显优势。 表2 控制截面动力可靠度计算结果Table2 Calculationresultsofdynamicreliabilityofcontrolsection控制截面传统响应面法神经网络算法动力可靠度迭代次数ANSYS求解次数动力可靠度迭代次数ANSYS求解次数边跨L/6截面6.686496.76433跨中截面8.528658.44649塔梁相交处截面9.2411899.321081 本文基于首次超越准则,构建了随机地震效应及结构参数随机性双重随机功能函数,并使用神经网络算法和虚拟激励法对某斜拉桥关键截面动力可靠度进行了求解,得到以下结论: a.桥梁结构抗震分析时需考虑地震随机性和结构参数随机性耦合作用效应,运用首次超越准则,以抗力和最大应力响应构建的双重随机非线性功能函数,能较为精确地描述结构在地震作用下的可靠度指标。 b.神经网络算法与响应面法计算得到的结构最小可靠度分别为6.68和6.76,两者仅相差1.2%,但神经网络算法迭代过程中调用ANSYS有限元结果的次数更低,迭代次数也更少,具有更快的拟合速度。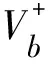
1.2 双重随机性功能函数构建
2 基于神经网络的功能函数求解方法
3 工程概况及有限元模型建立
3.1 工程概况


3.2 随机地震效应在ANSYS中的模拟

4 主梁动力可靠度分析结果



5 结论

