竖向地震动对钢-混组合梁桥地震易损性的影响分析

孔令才,王 华,刘世建

(1.桂西公路发展中心,广西 南宁 530000；2.广西交科集团有限公司,广西 南宁 530007)

水平地震动分量一直被认为是在地震分析中起着关键作用。然而，通过大量的震害调查和强地震动分析发现，竖向地震动分量在结构的损伤中也起着重要的角色，甚至直接引发严重震害。

竖向地震动分量主要引起桥墩轴力的急剧变化，桥墩的抗剪强度大大降低，造成桥墩的剪切破坏。Kunnath[1]等以公路立交桥为研究对象，得出了在竖向地震动作用下，柱中的轴力、梁中跨和盖梁处的弯矩均增大的结论。Mayes[2]等研究了竖向地震作用对公路桥梁地震反应的影响。结果表明，地震动的竖向分量对显著增加桥墩的轴力。随后，Kim[3]等发现，随着V/H的增大，桥梁墩顶的水平位移在一定范围内会显著增大，这将增加落梁的可能性；此外，桥墩的轴力将显著增加，从而大大降低其抗剪承载力，降幅达30%。Wilson[4]等进一步得到了斜弯桥在竖向地震动作用下比直桥更为脆弱的结论。

现行抗震设计规范中，竖向地震动对结构响应的影响一般按竖向加速度与水平加速度之比1/2～2/3考虑。然而，近年来的几次地震在断层附近记录到了强烈的竖向地震动，其中一些地震记录到的竖向加速度峰值甚至超过了水平加速度峰值。Bozorgnia[5]认为，竖向和水平向谱值的比取决于震源之间的距离，随着断层距离的增加而减小，该比值还受到地震震级和场地条件的影响。

结构地震易损性分析作为一种重要的概率地震风险评估方法，在许多工程结构中得到了广泛的应用。Gulerce[6]建立了一个考虑竖向地震动与水平地震动之比的概率地震需求模型。Wang[7]等研究了竖向地震动对固定支座的失效概率有很大影响。Wei[8]等研究了竖向地震动对高速铁路桥梁易损性的影响，发现大部分构件的损伤概率随着地震动竖向分量的增加而增加。近年来，刘洋[9]等对一座钢-混凝土组合桥梁进行了地震易损性分析，得出在近断层地震动激励下，桥梁的地震响应增大。

钢-混凝土组合梁桥由于结构轻盈，并且施工维护简单，因此在高速公路建设中得到越来越广泛的应用。而这些桥梁不可避免地将跨越发震断层，断层附近产生的较强的竖向地震动严重影响桥梁结构的地震响应。钢-混凝土组合梁桥的抗震性能一直是人们研究的重点，但考虑竖向地震动分量影响的文献仍较少。因此，本文将以基于性能的地震工程分析框架为指导，系统地分析竖向地震动分量对钢-混组合梁桥地震反应的影响。

1 算例桥梁

1.1 桥梁概述

选择一座跨度为4×35 m的钢-混凝土组合连续梁桥为案例，其总体布置如图1所示。其中工字形钢纵梁与端部横梁、中间横梁焊接成钢架，沿钢主梁上翼缘间距300 mm纵向布置直径22 mm、长度190 mm的ML15焊钉，将混凝土桥面与钢主梁连接成一个整体。桥墩选用C50空心截面，直径1.2 m，壁厚0.25 m。此外，在桥墩底部布置有圆形截面的C30混凝土群桩基础，并通过方形承台连接。

图1 钢-混组合梁桥总体布置图(单位：m)

1.2 动力有限元模型

基于OPENSEES平台，建立了考虑多种非线性效应的三维动态有限元模型。由于上部结构通常在地震作用下保持弹性，因此采用弹性板单元模拟混凝土板、弹性梁柱单元模拟工字钢梁。采用零长单元模拟混凝土板与钢梁之间的剪力钉，单个剪力钉的轴向刚度取值为销钉的轴向拉伸刚度，水平向考虑钉的滑移特性，采用基于OEHLERS提出的双折线本构曲线[10]，如图2所示，其中弹性阶段的剪切刚度表示为：

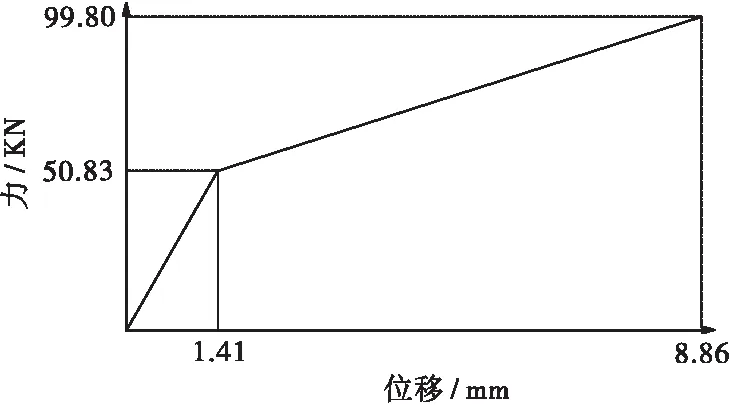
图2 基于OEHLERS法则的剪力钉水平向荷载-滑移曲线

(1)

开始滑移值：

δ=(80×10-3-86×10-5×fc)×dsh

(2)

极限滑移值：

δu=(0.48-0.004 2×fc)×dsh

(3)

式中:Pmax表示剪力钉抗剪强度设计值,kN;dsh表示销钉直径,mm;fc表示混凝土抗压强度设计值;α取值范围为0.08～0.24，当等于0.16时，代表平均抗剪刚度。

根据《钢-混凝土组合桥梁设计规程》[11]，抗剪强度计算为99.80 kN，平均抗剪刚度计算为36 kN/mm。

采用非线性梁柱单元模拟桥墩，将截面离散为混凝土保护层、混凝土核心层和钢筋层，混凝土本构为Mander模型，纵筋采用圆滑曲线的弹塑性本构。此外，选择零长度单元模拟支座，赋予ElasticPP材料。

由于地表土层较软，每个桩的顶部不考虑桩-土相互作用，通过采用0.5 m范围内的非线性梁-柱单元对每个单桩进行模拟。每个桩的其余部分需要考虑桩-土相互作用，并在上述0.5 m桩段底部用6个土弹簧模拟，包括3个平动弹簧和3个转动弹簧，弹簧刚度均通过传统的“m”法计算。

全桥固定阻尼比取0.035。表1列出前3阶周期振动模式。

2 分析方法

2.1 地震易损性理论

地震易损性是指结构在不同地震动强度(IM)下发生各种破坏状态的概率Pf。通常，构件地震需求(D)可以表示为IM的函数，并且假定二者服从对数正态分布关系，因此Pf表示如下：

Pf=P[D≥C|IM]=

(4)

式中:Φ[g]为标准正态函数;C为特定损伤状态的能力;SD和SC分别为需求和能力的中位值;βD和βC分别为其对数标准差，通过下式计算：

(5)

(6)

式中:Di为第i条地震波作用下非线性动力时程分析得到的动力响应；n为地震波总数；COV为构件抗震能力的变异系数，参考Nielson的研究[12]，轻度和中度损伤状态取0.25，严重和完全损伤状态取0.5。

2.2 地震动的选取

从PEER强震数据库中选取同Abdollah Shafie-ezadeh[13]在其文中使用80条实际地震波作为本文分析用的地震动，并将地震动竖向分量与水平分量的比值调整为0倍、0.5倍、1.0倍、1.5倍和2.0倍作为实际地震动输入。所选地震波具有如下特性：震级分布在5.5～7.0级范围，震中距分布在13～60 km范围，地震动峰值加速度(PGA)分布在0.032g～0.472g范围，具体分布如图3所示。

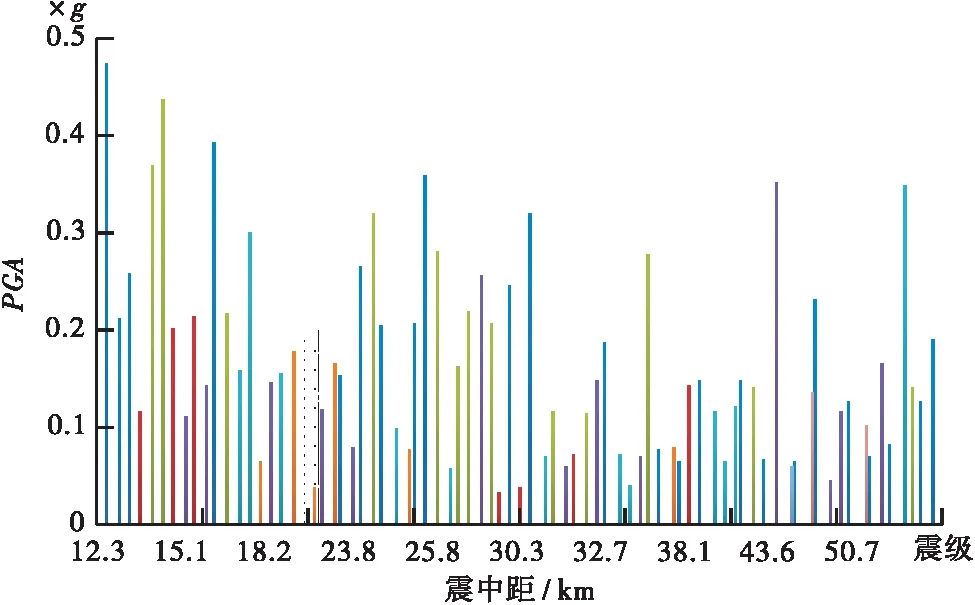
图3 所选地震波的震级以及震中距分布

2.3 地震动强度指标

最优地震动强度指标(IM)的选择是概率地震需求分析和易损性分析的关键步骤。在以往研究中，对于中小跨径桥梁，结构基本周期(Sa)处的谱加速度是最好的IM，如：WEI等[8]选择谱加速度(Sa)来评估高速铁路连续梁桥的地震易损性。另外，当Sa作为钢-混凝土组合桥梁的IM时，可降低概率地震需求模型的离散性[9]。因此，本文还选择Sa作为最优地震动强度指标，用以建立概率地震需求模型并进行后继地震易损性分析。

2.4 损伤指标

本研究以构件峰值响应作为工程需求参数，选择的工程需求参数包括：剪力钉位移、1号墩上的滑动支座位移、布置固定支座的3号墩墩底截面保护层混凝土应变以及3号墩下桩基础顶截面保护层混凝土应变。

通常将桥梁结构的损伤状态定义为完好无损、轻度损伤、中度损伤、严重损伤和倒塌5种状态。不同构件其对应表征损伤状态的指标不同，对于上述工程需求参数，本文参考已有研究中定义的损伤指标。

刘洋[9]等定义剪力钉的屈服位移为损伤参数，算例桥梁中的剪力钉计算的屈服位移为1.41 mm，定义为完好无损和轻度损伤的界限，其他损伤状态界限值列与表2中。由于桥墩和桩均是钢筋混凝土构件，故使用材料应变表征其损伤状态，这里仅使用截面的保护层混凝土应变[14]。相对位移可用于确定支座的损伤极限状态[8]，橡胶支座的设计位移为100 mm，因此定义支座完好至轻度损伤状态的界限值为100 mm，轻度和中度损伤的界限值为200 mm，中度和严重损伤状态的界限值为300 mm，严重至倒塌状态的界限值为400 mm。

表2总结了上述工程需求参数在5种损伤状态下的损伤界限值。

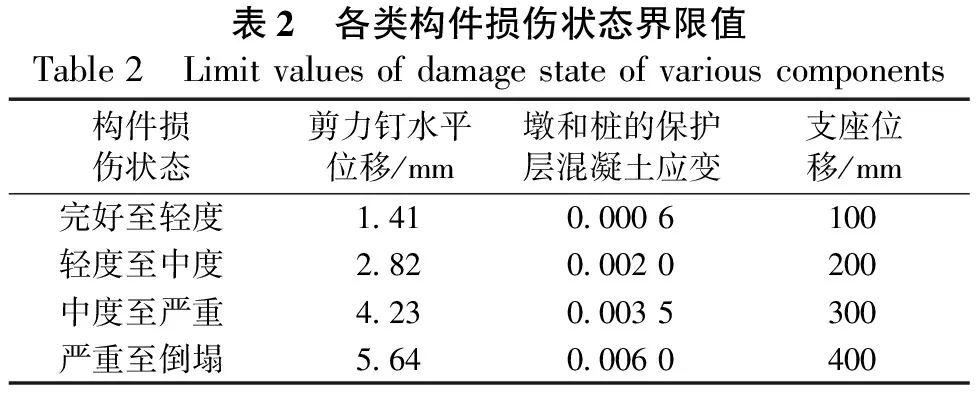
表2 各类构件损伤状态界限值Table2 Limitvaluesofdamagestateofvariouscomponents构件损伤状态剪力钉水平位移/mm墩和桩的保护层混凝土应变支座位移/mm完好至轻度1.410.0006100轻度至中度2.820.0020200中度至严重4.230.0035300严重至倒塌5.640.0060400

3 分析与讨论

以Sa作为地震动强度指标，根据式(4)计算出每个桥梁构件超越不同损伤状态的概率，获得易损性曲线并绘制在图4中。由于横桥向损伤特征与纵桥向损伤特征相似，限于篇幅，横向+竖向输入的计算结果此处未列出。

从图4中超越完好无损和轻微损伤状态的概率可以看出，在相同Sa下，支座的损伤超越概率最高，说明支座是最易损伤的构件；其次是桥墩以及群桩基础中最不利单桩；而剪力钉的损伤超越概率最低，这表明混凝土板与钢梁之间的剪力钉是最不易损构件。

(a)超越完好无损状态

3.1 剪力钉

图5(a)显示了不同组合地震动输入下，纵向+竖向地震作用时混凝土板和钢梁之间所有剪力钉的最大纵向相对位移的平均值。从图中可以看出，大多数位置的剪力钉纵桥向位移响应值小于屈服位移，即0.001 4 m，这表明剪力钉仍处于弹性工作状态；最大响应值出现在梁的左端，即0 m处。此外，当竖向地震分量与水平地震分量之比由0增大到2.0时，纵向位移响应明显增大。以0 m处为例，相对于单向地震输入，当竖/纵向地震动分量比从0.5增加到2.0时，剪力钉纵桥向位移分别增加了4.84%、11.29%、22.58%和28.23%。图5(b)显示了最大响应剪力钉(0 m位置)超越完好无损状态的易损性曲线，由图可知，剪力钉纵桥向上损伤超越概率随着Sa从0到2.0g而增加，随着垂直地震分量与水平地震分量之比从0到2.0而显著增加。以Sa=2.0g为例，当竖向地震动分量与水平向地震分量之比为0和2.0时，超越完好无损状态的概率分别为0.15%和5.31%，其原因是竖向地震动分量的增加引起了梁的竖向弯曲变形模式，使梁在纵桥向上有缩短的趋势，最终导致混凝土板和钢梁的相对位移增大。

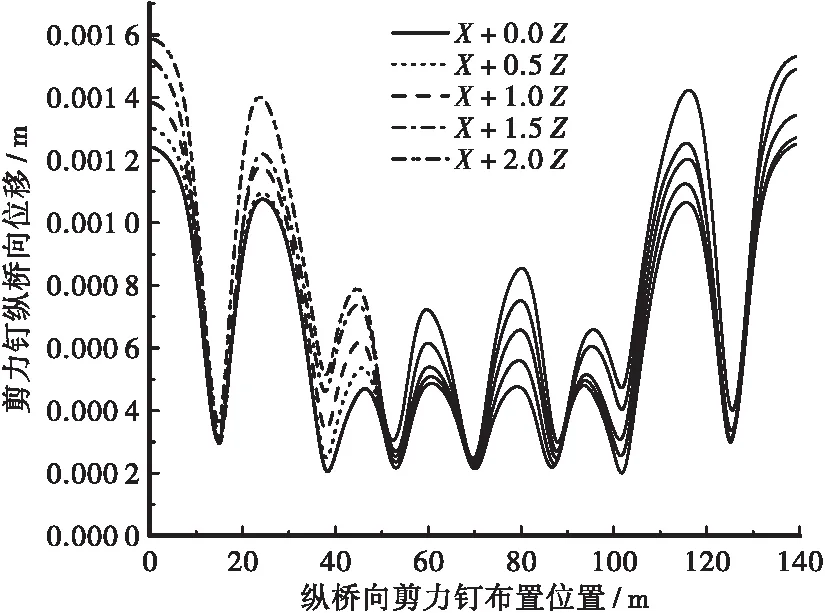
(a)剪力钉位移响应

3.2 支座

图6所示为1号桥墩处滑动支座超越完好无损状态的概率。当竖向地震分量与水平地震分量之比从0到2.0时，超越概率没有显著增加。虽然竖向地震动激发了梁的多种竖向弯曲变形模式，但对于主梁来说，主梁的纵向振动并没有得到加强，因此，相对位移没有显著增加。此外，由竖向地震分量引起的其他位置支座的损伤概率的变化也很小，故此处未列出所有支座的响应。

图6 纵向+竖向地震作用下支座易损性曲线

3.3 墩和桩

由于固定支座传递的上部结构惯性力最大，故布置固定支座的3号墩是所有桥墩中损坏最严重的。因此，图7显示了3号桥墩底部保护层混凝土在纵桥向超越完好无损状态的概率。此外，图8也列出了3号桥墩下最不利保护层混凝土在纵桥向超越完好无损状态的概率。从图7和图8可以清晰看出，PGA从0增加到2.0g会增加保护层混凝土应变的损伤概率。另一种现象是桥墩和桩的损伤概率随竖向地震动分量的增大而显著增大，且随着PGA的增大而增大。具体地说，当Sa=2.0g，竖向地震分量与水平分量之比为0和2.0时，桥墩超越完好无损状态的概率分别为25.89%和73.88%，这是由于竖向地震动引起上部结构的竖向振动，增加了桥墩和桩的竖向压力，从而增加了保护层混凝土的损伤概率。

图7 纵向+竖向地震作用下3号桥墩的易损性曲线

图8 纵向+竖向地震作用下3号桥墩最不利单桩的易损性曲线

上述研究表明，其他桥墩比3号桥墩更安全，地震作用下桥墩底部仅发生轻微的保护层混凝土破坏。因此，这里没有列出所有较小的响应值。

4 结论

基于易损性分析方法，研究了不同竖向地震动分量比对钢-混凝土组合梁桥地震响应以及损伤的影响。现总结如下：

a.在地震作用下，支座比其他部件更容易损坏，而剪力钉的大部分响应值小于屈服位移，是最不易受损构件。

b.竖向地震动分量与水平地震动分量之比的增大会显著增大剪力钉、桥墩和桩基础构件的损伤概率，且这种趋势在PGA增大时更为显著，但对支座损伤影响甚微。

c.钢-混凝土组合梁桥的抗震设计中应考虑地震动的竖向分量。