钢-UHPC组合桥面板UHPC层受力性能研究

马 帅， 张士红， 邵旭东

(1.河南省交通运输发展集团有限公司，河南 郑州 450016； 2.河南省交通规划设计研究院股份有限公司，河南 郑州 450018； 3.湖南大学，湖南 长沙 410082)

开口肋和闭口肋是钢桥面板两类最基本的结构形式[1]，二者在局部车轮荷载传递效率、疲劳性能和经济性等方面各具优势，有不同的工程适用范围[2]，相关学者对此已做过大量而深入的研究[3-5]。

文献[6-7]分别提出将具有高强和高韧性的UHPC层通过栓钉连接件与钢板连接，形成两类新型组合桥面板——带U肋和带开口肋的钢-UHPC组合桥面板，以解决传统钢桥面板疲劳开裂的难题。UHPC层的静力强度、疲劳性能以及层间粘结状态等是钢-UHPC组合桥面板的重要设计参数，对组合结构性能的发挥至关重要。已有研究[6-10]均针对单一纵肋形式的钢-UHPC组合桥面板，较少涉及两类钢-UHPC组合桥面板受力性能的对比分析。本文首先采用有限元方法对两类钢-UHPC组合桥面板的UHPC层受力特性对比分析，然后提出了UHPC层横桥向简化计算模型及计算方法，最后对影响UHPC层受力的关键受力因素进行参数分析，得到一些有益结论，供工程设计参考。

1 有限元模型

1.1 两类钢-UHPC组合桥面板

按照截面面积、纵桥向抗弯惯性矩及形心位置均保持一致的原则[4]，将一个U肋等效为两个倒T肋，试设计两种纵肋形式的钢-UHPC组合桥面板结构体系，如图1所示：两类钢-UHPC组合桥面板的钢顶板均厚12 mm，横肋高1.5 m，每隔2.4 m设一道16 mm厚横隔板。其中，U肋间距为600 mm，则相应的倒T肋间距为300 mm。钢顶板上焊接直径为13 mm，高度为35 mm，间距为200 mm×200 mm(纵向×横向)的栓钉，与50 mm厚的UHPC层连接形成受力整体。为减少其他设计参数可能对计算结果的影响，两类钢-UHPC组合桥面板体系的其它构造尺寸等均保持相同。

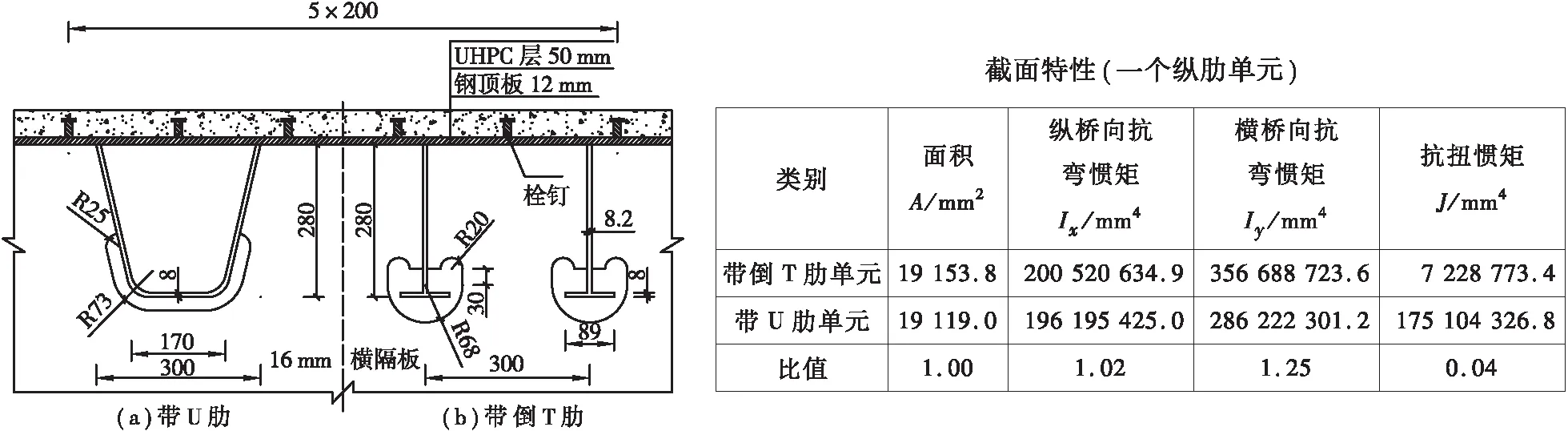
图1 钢-UHPC组合桥面板构造尺寸(单位：mm)

1.2 局部有限元模型及计算参数

采用大型通用有限元软件ANSYS分别建立带U肋和带倒T肋的钢-UHPC组合桥面板的局部有限元模型，见图2。两个有限元模型的纵向包含3个横隔板，横向包括8(16)个U(倒T)肋。局部有限元模型中，采用SHELL91模拟钢板，采用SOLID95单元模拟UHPC层。为降低计算规模，在建立有限元模型时，将需要关注区域的进行网格尺寸细化至1 mm左右，其它非关注区域采用较大尺寸的有限元网格进行划分。有限元计算中假设UHPC层为连续、均匀、各向同性的弹性体[7]，且忽略UHPC层与钢顶板之间的微小滑移。

图2 局部有限元模型

由于本文主要研究钢-UHPC组合桥面板第二、三体系的受力特性，因此主要研究车辆荷载作用下的结构受力，汽车荷载的相关参数依据文献[11]规定进行取值。由于钢桥面板的应力分布局部性较强[1]，仅采用标准车的单轮进行加载。有限元模型的边界条件参考文献[12]进行施加。

不同的车辆荷载与纵横肋的位置关系，均产生不同的应力结果，有限元局部计算考虑全部荷载工况不太现实，因此，本文选取典型荷载工况进行分析：车辆荷载沿纵桥向每次移动50 mm从横隔板正上方至跨中位置，即从纵向荷位1移动至纵向荷位25，见图3(a)；车辆荷载沿横向移动，与纵肋形成3种相对位置关系，分别为横向荷位1、2和3，见图3(b)。分别计算两类钢-UHPC组合桥面板75种荷载工况下，UHPC层的力学指标。需要说明的是，对于带倒T肋的钢-UHPC组合桥面板来说，在规范轮载作用下横向荷位1和横向荷位3是等效的。

图3 加载工况(单位：mm)

2 UHPC层受力性能

车辆荷载作用下，支撑于纵、横肋上的组合桥面板承受正负弯矩作用，位于结构层上方的UHPC层面临因抗拉强度不足或层间抗剪不足而发生破坏的风险。因此，实际工程中需重点关注UHPC层的横桥向拉应力、纵桥向拉应力和UHPC层间剪应力共计3项力学指标。下文对两类钢-UHPC组合桥面板的上述力学指标进行对比分析。

2.1 计算结果对比

计算得到两类钢-UHPC组合桥面板在共计75种车辆荷载工况下，UHPC层的纵、横桥拉应力及层间剪应力计算结果如图4～图6所示。其中，“U-top”指带U肋的钢-UHPC组合桥面板UHPC层顶面的拉应力；“U-bot”指带U肋的钢-UHPC组合桥面板UHPC层底面的拉应力；“Sx”指UHPC层的横桥向拉应力；“Sz”指UHPC层的纵桥向拉应力；“U-Sxy”指带U肋的钢-UHPC组合桥面板的横桥向层间剪应力；“U-Syz”指带U肋的钢-UHPC组合桥面板纵桥向层间剪应力，其余参数含义类比。

由图4～图6可知，对于两类钢-UHPC组合桥面板：①荷载位置(包括横向荷位和纵向荷位)和结构形式(带U肋和带倒T肋)均影响UHPC层的受力；②对比UHPC层力学指标随荷载位置变化可知，横桥向力学指标变化规律差异明显，但纵桥向力学指标变化规律差别较小。③UHPC层的上顶面普遍比下底面受力更不利，且纵桥向拉应力普遍比横桥大；④UHPC层横桥向层间剪应力普遍比纵桥向大，且带U肋的钢-UHPC组合桥面板层间剪应力普遍比带倒T肋的大。

将图4～图6的主要计算结果整理汇总，如表1所示。

图4 横向荷位1计算结果

图5 横向荷位2计算结果

图6 横向荷位3计算结果

表1 计算结果汇总Table1 SummaryofcalculationsMPa类别SxSztop面bot面top面bot面SxySyz带U肋的钢-UHPC组合桥面板2.531.673.600.862.741.94带倒T肋的钢-UHPC组合桥面板1.591.553.050.781.491.51比值1.591.081.181.101.841.28

由表1可知，截面面积、纵桥向抗弯惯性矩及形心位置均相同的带U肋和带倒T肋的钢-UHPC组合桥面板的UHPC层受力指标对比表明：① 带U肋的钢-UHPC组合桥面板UHPC层受力更不利，尤其是横桥向力学指标(包括UHPC的横桥向拉应力、横桥向层间剪应力)比纵桥向更不利；② UHPC层的设计主要受纵桥向拉应力和横桥向层间剪应力控制。

2.2 横桥向计算模型

钢-UHPC组合桥面板是复杂的空间受力结构，一般采用有限元方法进行UHPC层的受力分析。但有限元方法仅能提供离散的数值解，难以得到结构作用机理的闭式解，且不便于工程应用。下文基于结构力学方法，将空间桥面板等效为横向连续梁进行受力分析。

研究表明，钢桥面板横向影响线长度在3个U肋间距左右，纵向影响线长度为3个横隔板间距长度[13]。这里取钢-UHPC组合桥面板的单条纵肋进行研究，将沿纵向弯曲的一条纵肋简化为三跨简支梁。设单个纵肋的纵桥向截面抗弯刚度为EsIr，横隔板间距为L。其中，Es为钢材的弹性模量；Ir为一条纵肋的纵桥向抗弯惯性矩。基于单位荷载法，计算得到单条纵肋沿纵桥向的弹性支承刚度为K0=1 200EsIr/23L3。

参考文献[12]可知，三跨连续梁跨中截面的弯矩影响线为2次曲线。构造一个横隔板间距长度的纵向集中荷载对跨中截面弯矩的影响曲线，计算得到单位集中荷载的影响系数μ：

(1)

对于单轮纵桥向接地长度为b=200 mm的标准车辆荷载，在最不利荷载位置时钢-UHPC组合板的有效分布宽度参考文献[14]进行计算，即b0=b+l/3=300 mm，其中l为纵肋支撑间距，本例中l=300 mm。将b0=300 mm，L=2 400 mm带入式(1)中可得：μ=0.91。从而计算得到每条纵肋的等效弹性支承刚度K=μK0=1 200μEsIr/23L3，横桥向荷载集度q=140×103÷2÷600=116.67 N/mm。

上文已指出钢桥面板的横向影响线长度在3个U肋间距左右[13]，这里横桥向计算取5(10)个U(倒T)肋间距的钢-UHPC组合桥面板单元作为研究对象，简化成如图3所示的7跨弹性支撑组合梁模型。采用结构力学方法容易得到组合梁各个截面内力值，如图7所示。

图7 内力图

得到各个截面的内力后，采用换算截面法容易得到包括UHPC层的横桥向应力和层间剪应力大小在内的UHPC层各项力学指标，计算式为：

(2)

(3)

式中:y为UHPC顶面距离组合截面中心的距离；n为钢材的弹性模量与UHPC的弹性模量之比，即n=Es/Ec；S0为UHPC层对整个截面的面积矩；b0为组合板的计算宽度；I0为组合梁的惯性矩，满足：

(4)

在最不利荷载位置(横向荷位1、纵向荷位25)工况下，基于式(2)、式(3)和有限元方法得到的两类钢-UHPC组合桥面板UHPC上顶面横桥向应力和层间剪应力值对比如图8所示。

为验证不同肋间距时，上述计算方法的适用性和计算精度，分别计算纵肋间距l=300、400、600、800 mm时，UHPC顶面横桥向应力最大值Sx和横桥向层间剪应力最大值Sxy，计算结果如表2所示。其中，有限元值采用带U肋的钢-UHPC组合桥面板计算结果。

由图8和表2的计算结果可知：①UHPC顶面横桥向应力最大值与有限元值最大值差别较大，而UHPC层间剪应力计算最大值与有限元值最大值差别较小，但本文方法和有限元结果总体上相吻合；②对于不同肋间距，本文计算方法均具有适用性，尤其是对UHPC横桥向层间剪应力值精度较高。其中，本文提出的横桥向简化计算模型的误差主要来源于以下几个方面：纵桥向计算时，将纵向弹性支撑在横隔板上的纵肋简化为三跨连续梁具有近似性；组合板基于文献[14]方法计算得到的有效工作宽度值偏小；本文解析方法得到层间剪应力值是组合板有效工作宽度上的平均值，而有限元方法得到的是最大值。

图8 计算值与有限元值对比

表2 计算结果汇总Tab.2 Summaryofcalculations纵肋间距l/mm组合板计算宽度(b0=b+l/3)/mm应力峰值/MPa本文方法有限元值SxSxySxSxy差值率/%SxSxy3003002.861.321.871.2452.96.5400333.32.721.581.901.6443.2-3.76004004.091.983.282.1224.7-6.6800466.77.261.695.411.7534.2-3.4

3 UHPC层参数分析

UHPC层作为钢-UHPC组合桥面板的结构层参与受力，其受力特性不仅与钢桥面板的结构设计参数息息相关，且受UHPC层自身设计参数的影响：UHPC层厚度影响桥梁结构的上部自重和工程经济性；UHPC层间粘结状态对UHPC层自身和钢结构的受力性能影响显著。现有文献针对上述两个设计参数对UHPC层自身受力性能的影响较缺乏。下文以带U肋的钢-UHPC组合桥面板为例，分别探究UHPC层厚度和层间粘结状态两个设计参数对UHPC层受力性能的影响。

3.1 UHPC厚度

UHPC层厚度对结构的受力和造价影响较大，是钢-UHPC组合桥面板的关键设计参数[10]。为分析不同UHPC厚度对其自身应力的影响，建立不同UHPC厚度(40、50、60、70 mm)的带U肋的钢-UHPC组合桥面板有限元模型，有限元建模及加载方式参考1.2节，计算得到不同UHPC厚度时UHPC层纵、横向拉应力峰值及层间剪应力峰值，如图9所示。

图9 参数1计算结果

由图9可知：①随着UHPC层厚度的增加，其纵、横向拉应力及层间剪应力值均减小，但UHPC层下底面的纵、横向拉应力峰值变化幅度较小。②当UHPC厚度增加至50 mm时，应力变化趋于平缓。对于常规的钢-UHPC组合桥面板，UHPC层厚度宜取50～70 mm。

3.2 层间粘结状态

UHPC层与钢桥面板之间一般采用栓钉连接件来承担界面之间的剪力作用[10]。研究表明[16]，组合桥面板的混凝土层与钢板之间的结合程度对结构的受力会产生较大的影响。本文考虑UHPC层与钢板从滑移到完全结合，不同结合程度时UHPC层的应力峰值。有限元模型中栓钉连接件采用COMBINE14单元模拟布置间距为为200 mm×200 mm(纵向×横向)的栓钉，栓钉之外的位置耦合UHPC层与钢顶板之间的竖向位移，其余部分有限元建模及加载方式同1.2节。由于栓钉连接件没有方向性，COMBINE14单元的纵桥向和横桥向刚度设置为相同数值。

计算栓钉的抗剪刚度K从0～∞变化时，UHPC层的拉应力峰值，如图10所示。可知：①随着UHPC层与钢顶板的结合程度增加，UHPC层上顶面的纵、横向拉应力值呈降低趋势；②由于栓钉与UHPC层连接位置存在应力集中，局部轮载作用下UHPC层下底面的纵、横向拉应力值较大，且随着栓钉刚度的增大，应力值缓慢增加；③UHPC层与钢顶板完全结合无滑移时，UHPC层顶、底面的纵、横向拉应力值降至最小。因此，有限元计算时不考虑UHPC层与钢顶板之间的滑移效应，对于UHPC层设计偏不安全。

图10 参数2计算结果

4 结论

本文在采用有限元方法对两类钢-UHPC组合桥面板的UHPC层受力性能对比分析基础上，又基于传统结构力学方法提出了UHPC层横桥向简化计算模型及计算方法，最后对UHPC层厚度和UHPC层粘结状态两个设计参数进行有限元分析，得到如下主要结论。

a.截面面积、纵桥向抗弯惯性矩及形心位置均相同的带U肋和带倒T肋的两类钢-UHPC组合桥面板的UHPC层3项力学指标对比表明，两类钢-UHPC组合桥面板的UHPC层纵、横向拉应力及层间剪应力在数值大小、变化规律上均存在一定的差异，且带U肋的钢-UHPC组合桥面板的UHPC层受力更不利。

b.基于传统结构力学方法提出的UHPC层横桥向计算模型得到的计算值与有限元结果吻合度高，具有一定的工程实用性。

c.适当增加UHPC层厚度，能有效降低纵、横向拉应力及层间剪应力值，合理的UHPC层厚度宜取50～70mm。

d.对于钢-UHPC组合桥面板结构来说，有限元计算时不考虑UHPC层与钢顶板之间的滑移效应，对于UHPC层的设计偏不安全。