体外预应力加固钢筋混凝土简支梁的设计参数研究

毛德均， 许 鹏， 陈 旭， 莫南明

(1.昆明学院 建筑工程学院，云南 昆明 650214； 2.云南通衢工程检测有限公司，云南 昆明 650041)

0 引言

国内大量早期修建的公路钢筋混凝土(RC)简支梁桥由于技术标准低、服役时间长，存在严重损伤和病害，需加固以继续为经济社会发展服务。体外预应力加固指通过施加体外预应力，使原结构、构件的受力得到改善或调整的方法[1]。该加固法具有自重轻、加固效果好、施工工艺简单、检测维修方便等优点，在桥梁加固中得到了广泛应用[2-4]。加固设计往往是基于桥梁实际技术状况，通过一些可变设计参数的合理取值和组合来获取比较理想的加固效果[5]。就体外预应力加固RC简支梁桥来说，可变的设计参数主要为钢束型号、张拉控制力、钢束用量、钢束转向位置、钢束转向角度、钢束距梁底距离和钢束距梁侧面距离。显然，参数取值不同得到的加固效果存在差异，由于我国现行《公路桥梁加固设计规范》(JTG/T J22-2008)[1]对上述加固参数的设计取值大都没有明确规定或建议，导致加固设计不可避免地具有一定经验性，因此，开展设计参数对加固效果的影响研究具有重要价值。

文献[6]在分析了加固构件抗弯刚度的基础上，提出了体外预应力加固RC混凝土简支梁反拱挠度的计算方法。文献[7]采用直接计算承载力增量的方法，对体外预应力钢束所提供的承载力增量进行了计算分析。文献[8-9]通过建立体外预应力加固试验模型，对裂缝发展、承载能力等开展研究，证明了体外预应力在改善裂缝和提高构件承载力方面的优势。文献[10]开展了CFRP筋体外预应力加固铁路PC简支梁桥的加固设计和现场试验。文献[11]开展了16片体外预应力加固RC简支梁的试验研究，主要探讨了直线布筋和折线布筋形式对加固效果的影响。文献[12]开展了3片体外预应力加固不同损伤程度RC简支T梁的静力破坏试验，在试验研究的基础上，采用有限元扩大参数分析，研究了预应力度、混凝土强度等级、预应力筋截面面积以及预应力筋位置对加固构件承载性能的影响，但每种参数变量设置数量偏少，仅为3～5个。文献[13]通过试验研究和有限元扩大参数分析，研究了张拉控制力和钢束形心距梁底距离(简称束高)对体外预应力加固RC简支梁承载性能的影响。不难发现，既有研究采用的手段涵盖了试验、理论和有限元数值模拟，研究内容主要为体外预应力加固RC简支梁的力学行为，对加固参数的研究虽有涉及，但参数类型涵盖不够全面，参数变量设置代表性不够。

鉴于此，本文采用ANSYS软件建立分离式有限元模型，对文献[13]开展的试验研究进行了数值模拟，将有限元计算得出的试件极限承载力、破坏形态和荷载-位移曲线与试验结果进行对比分析，以验证有限元模型的合理性，在有限元结果可靠性得到充分验证的基础上，通过合理设置参数取值进行扩大参数分析，研究了钢束截面面积Ap、转向器位置、钢束转向角度θp、钢束形心距梁侧面距离Hd对加固梁承载性能的影响。本次研究作为文献[13]研究内容的扩展延伸，结论可为相关人员更加深入地了解体外预应力加固RC简支梁的受力行为和开展加固设计提供参考。

1 文献试验设计概况

文献[13]试验研究的试件体外预应力加固示意如图1所示，试验梁计算跨径L=2 000 mm，加固前试件不作预裂损伤，预应力钢筋采用1×7标准型φ15.2低松弛钢束，梁体两侧各对称布置1根，单根钢束截面面积Ap=139 mm2，钢束形心距梁侧面的距离Hd为30 mm，在距支点L/4处设置2个转向器转向，单端张拉锚固于支座上方，转向器和锚固块的材质均为钢材。试件主要设计参数见表1。

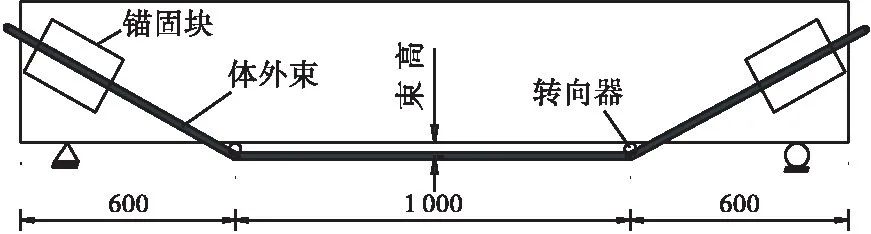
图1 试件体外预应力加固示意(单位：mm)

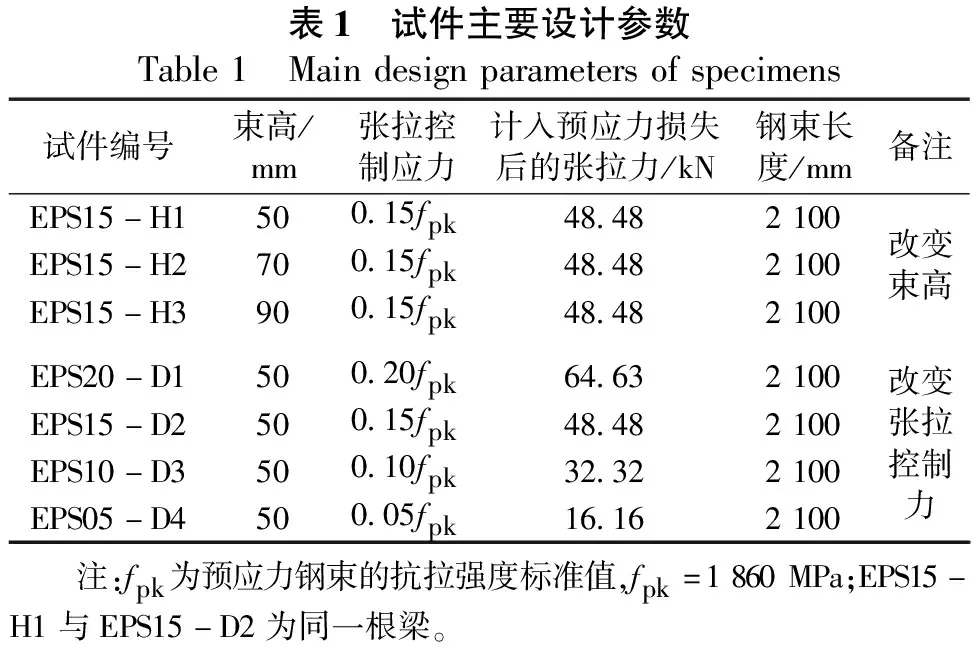
表1 试件主要设计参数Table1 Maindesignparametersofspecimens试件编号束高/mm张拉控制应力计入预应力损失后的张拉力/kN钢束长度/mm备注EPS15-H1500.15fpk48.482100EPS15-H2700.15fpk48.482100改变束高EPS15-H3900.15fpk48.482100EPS20-D1500.20fpk64.632100改变张拉控制力EPS15-D2500.15fpk48.482100EPS10-D3500.10fpk32.322100EPS05-D4500.05fpk16.162100 注:fpk为预应力钢束的抗拉强度标准值,fpk=1860MPa;EPS15-H1与EPS15-D2为同一根梁。

文献[13]并未明确给出钢束转向角度θp值，根据其给出的相关尺寸推算出θp≈20°，各试件的θp为定值。试件配筋构造如图2所示，纵筋为φ12HRB400带肋钢筋；箍筋为φ8R235光圆钢筋，试验采用三分点加载，试件主要材料参数见文献[13]。

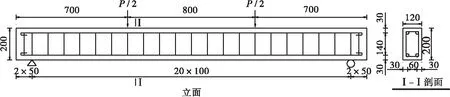
图2 试件配筋构造(单位：mm)

2 有限元模型建立及计算结果验证

2.1 单元类型及材料本构关系

本文用ANSYS13.0建立分离式有限元模型。其中，混凝土采用SOLID65单元，其材料模型采用多线性随动强化模型(KINH)，单轴应力-应变曲线采用GB50010-2010中的上升段和Hognestad公式下降段的组合，破坏特性描述方式为W-W五参数屈服准则(CONCR)，关闭混凝土压碎检查。有限元模型中混凝土所需的材料参数有弹性模量Ec、泊松比νc、开裂剪力传递系数βt、闭合剪力传递系数βc、轴心抗拉强度ft、轴心抗压强度fc[13-14]。

普通钢筋采用LINK8单元，预应力筋采用只能承受单向拉伸、压缩的LINK10单元。钢筋材料模型采用双线性等向强化模型(BISO)，应力-应变曲线采用理想弹塑性模型。有限元模型建立时普通钢筋需要的材料参数有抗拉屈服强度fy、弹性模量Es及泊松比νs；预应力筋所需材料参数有抗拉屈服强度fpy、弹性模量Epe和泊松比νps。锚固块和转向器采用SOLID45单元，材质为钢材，不考虑材料非线性，有限元模型建立时所需的材料参数有弹性模量Emz和泊松比νmz。

有限元模型建立所需的上述材料参数，大部分文献[13]已经给出，凡已给出者均按给出值取用，未给出者参考相关文献进行取值[5，14-15]。

2.2 网格划分和边界条件

有限元模型的单元尺寸对计算过程和结果都有重要影响，不宜过大或过小，本文的单元尺寸控制在5 cm以内。网格划分完成后的有限元计算模型见图3所示，整个计算模型共有4 771个节点、3 268个单元。

(a)普通钢筋

对梁一侧支点单元节点施加x、y、z方向的平动约束，另一侧支点单元节点施加y、z方向平动自由度，实现简支条件的模拟。不考虑普通钢筋与混凝土之间的粘结滑移，通过控制网格划分在钢筋与混凝土之间建立重合节点，耦合重合节点x、y、z方向的平动自由度实现。

不考虑体外束与锚固块之间的相对滑移和挤压作用，将力筋与锚固块的相邻节点进行自由度耦合。体外束在转向器处发生偏转，体外束与转向器沿梁纵向的接触处理方式通常有两种，一种是自由滑动，另一种是摩擦接触[13]，本文采用自由滑动。

2.3 加载方式及求解设置

采用等效应变法施加预应力，具体方法为在预应力筋所属的钢筋单元中，对其实常数(Real)的初始应变(ISTRN)进行定义，使预应力钢筋产生与预应力效应相当的应变，然后将实常数赋予预应力钢筋单元。试验荷载采用节点群面荷载(SF)方式施加，以斜坡荷载(Ramped Loads)形式施加。在加载位置设置弹性垫块，其材料性质与锚固块、转向器相同，以避免加载区域应力集中导致模型提前失效。

极限荷载的求解方式采用与文献[5]相同的方法。有限元分析类型(ANTYPE)为静态分析，采用完全的Newton-Raphson法求解、力收敛控制准则、收敛误差放宽到5%、2范数控制收敛，打开大变形效应(NLGEOM)和线性搜索(LNSRCH)，其余设置采用ANSYS的默认设置。

2.4 计算结果验证

根据文献[13]的试验结果情况，取有限元计算得到的代表性结果与试验结果进行对比分析，以验证有限元模型的可靠性。试验梁的承载力试验值与有限元计算值对比见表2，由表2可知，承载力计算值比试验值偏大，二者偏差在4%～15%以内。通常，当承载力的有限元计算值和实测值的偏差在20%以内时，可以认为计算值具有一定的参考价值[5]。

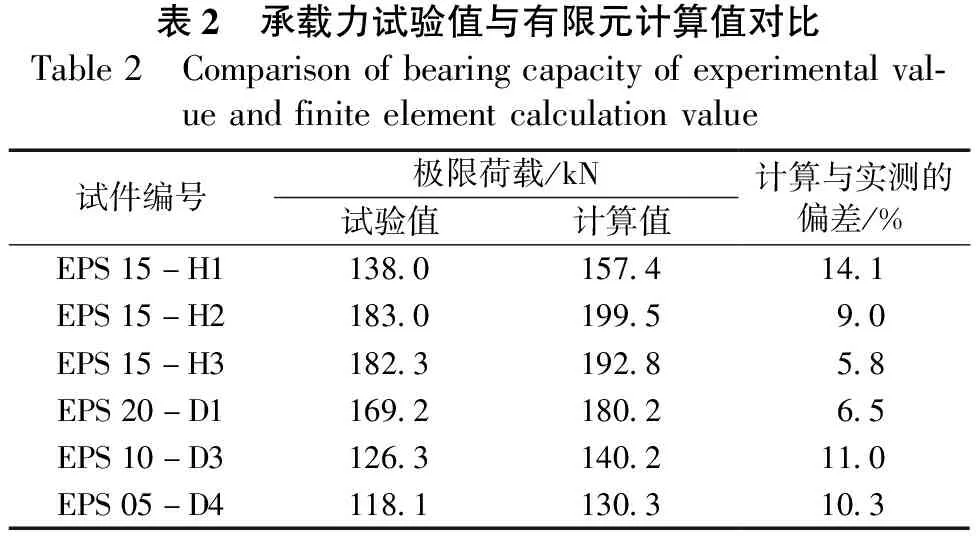
表2 承载力试验值与有限元计算值对比Table2 Comparisonofbearingcapacityofexperimentalval-ueandfiniteelementcalculationvalue试件编号极限荷载/kN试验值计算值计算与实测的偏差/%EPS15-H1138.0157.414.1EPS15-H2183.0199.59.0EPS15-H3182.3192.85.8EPS20-D1169.2180.26.5EPS10-D3126.3140.211.0EPS05-D4118.1130.310.3

试验试件由于参数设置不同而存在差异，但总体受力情况相同，试验结果表明，所有试件均表现为RC受弯梁的典型破坏特点，即受拉区混凝土竖向开裂、受拉区普通钢筋屈服、受压区混凝土压碎。有限元计算得出的所有试件破坏情况也表现为以上特点，现以EPS15-H1为例进行说明。试验过程中EPS15-H1在外荷载达到138.0 kN时梁体因受压区混凝土压碎而破坏，此时梁体受拉钢筋应力达到屈服强度442 MPa，钢束拉应力为442 MPa，跨中梁顶混凝土压碎起皮区域的混凝土压应变达到3 544 με；以上指标有限元计算得出的值相应为447 MPa、511 MPa和3 706 με，有限元结果与试验结果吻合较好。

EPS15-H1的荷载-位移(P-Δp)曲线对比如图4所示，从图4可见，P-Δp曲线的试验值大于有限元计算值，且有限元未得出曲线下降段，但二者变化规律相同，曲线可分为3段，分别为开裂前的弹性工作阶段、开裂后的带裂缝工作阶段和逐渐破坏至完全破坏阶段。总体看，EPS15-H1的P-Δp曲线有限元计算结果与试验结果符合较好。

图4 EPS15-H1的P-Δp曲线

以上验证表明本文建立的有限元模型总体上能够较好地模拟试验梁的实际受力情况，计算结果精度满足工程分析要求。

3 设计参数研究

以试件EPS15-H1为基本对象，在其基础上改变对象参数取值进行扩大参数分析，结果分析以加固构件的极限承载力Pu为主，以其他相关结果为辅，主要研究参数取值对构件承载性能的影响。

3.1 钢束截面面积Ap

JTG/T J22-2008的8.2.4第3条规定，体外预应力的张拉控制应力σcon≤0.65fpk。采用体外预应力加固时，被加固构件的承载性能和外部环境条件存在较大差异，通常需要结合实际情况，在钢束布置形式确定后，通过灵活采用σcon值和钢束用量来获取适当的体外预应力值，以获取较为理想的加固效果。由于σcon受限，当需要较大的体外预应力时，就需在σcon及其他参数都确定的条件下，通过增大钢束用量来实现，钢束用量变化通过改变钢束截面面积Ap实现。本文Ap的参数设置及Pu的计算结果见表3，根据表中数据，绘制了Pu随Ap的变化趋势见图5。

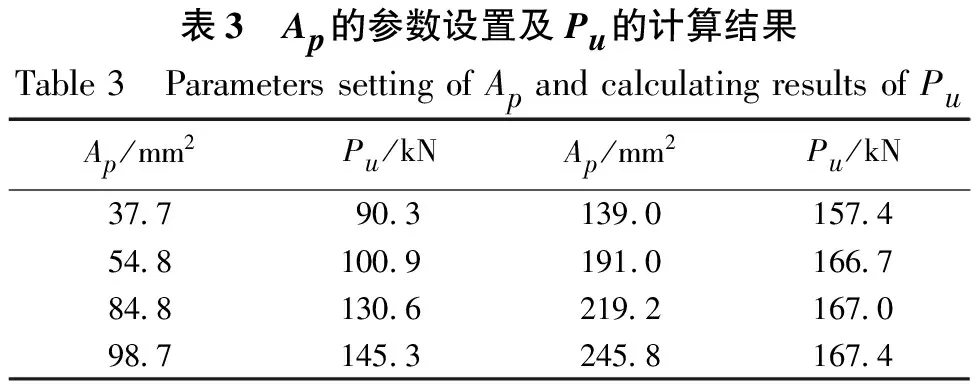
表3 Ap的参数设置及Pu的计算结果Table3 ParameterssettingofApandcalculatingresultsofPuAp/mm2Pu/kNAp/mm2Pu/kN37.790.3139.0157.454.8100.9191.0166.784.8130.6219.2167.098.7145.3245.8167.4

图5 Pu随Ap的变化趋势

结合表3和图5可知：Ap对Pu有明显影响，二者关系曲线表现为Ap较小时，Pu相对提升幅度较小，此时曲线趋于平缓、斜率较小，见曲线左起第1点至第2点之间的区段；随着Ap增大，Pu相对提升幅度逐渐变大，此时曲线逐渐变陡、斜率增大，见曲线左起第2点至第4点之间的区段；随着Ap进一步增大，Pu相对提升幅度转而变小，曲线又趋于平缓，表明Pu的提升幅度在逐渐减小，原因是Pu逐渐达到采用体外预应力加固的“回归值”(也可称为“极限值”，在此为与极限承载力区分，将其称为“回归值”)，此后继续增大Ap收效甚微。同时，随着Ap增大，构件达到Pu时的钢束应力σp在逐渐降低，从Ap=37.7时σp=822 MPa逐渐降低为Ap=245.8时σp=340 MPa，这反映出增大Ap将导致钢束强度发挥程度逐渐降低，造成不同程度的材料浪费。

根据上述分析结果可知，随着钢束截面面积Ap的增大，Pu存在“回归值”，相应地存在最佳钢束用量。钢束用量偏大、偏小对Pu的提升效果均不够理想。对试件EPS15-H1而言，其最佳钢束用量的Ap为130～160 mm2，不同构件具体情况存在差异。实际加固时，可根据被加固构件的承载性能，在σcon和钢束布置形式确定后，通过获取加固构件的Pu“回归值”来确定最佳钢束用量。具体操作时，可将钢束用量从小往大调整进行试算，得出Pu-Ap曲线，进而确定最佳钢束用量。

3.2 转向器位置

转向器在体外预应力结构中有重要作用，在担负预应力筋转向任务的同时，和锚固块一同构成体外预应力筋与主梁的紧密联系。从工程加固实例看，简支梁的转向器数量通常设置0个、1个或2个，0个为直线布束，1个时转向器多设置于主梁L/2处，2个时转向器位置则相对较灵活。文献[11]指出，理论上简支梁转向器应设置于剪力最大或应力剧变处，实际工程难免和理论存在偏差。显然，在其他参数确定的情况下，转向器位置对Pu有影响。有研究表明[3]，简支梁设置2个转向器加固效果比设置1个好，不设转向器时加固效果最差，实际工程多采用两个转向器。本文转向器位置变化通过改变转向器到支点的水平距离ld实现，ld的参数设置及Pu的计算结果见表4，根据表中数据，绘制了Pu随ld的变化趋势见图6。

表4 ld的参数设置及Pu的计算结果Table4 ParameterssettingofldandcalculatingresultsofPuld/mmPu/kNld/mmPu/kN325132.4550147.7350164.1575142.2375174.5600137.5400173.2625132.7425170.5650126.5450165.9675120.8475161.3700114.5500157.4725109.4525152.8750104.7

图6 Pu随ld的变化趋势

结合表4和图6可知：ld对Pu有明显影响，Pu存在峰值点，ld过大、过小时，Pu都相对较小。与水平布束和L/2位置处的1个转向器布束方式相比，本文模型中2个转向器的ld越小就越接近于直线布束，ld越大就越接近于1个转向器布束，这两种布束方式均不够理想，原因是二次效应的不利影响。体外预应力钢束在相邻锚具或转向器之间保持直线，当梁体在外荷载作用下发生挠曲变形时，相邻锚具或转向器之间的钢束偏心距会发生变化，此为二次效应。二次效应会降低梁的刚度和承载能力，且随梁挠度增大而增大[16-18]。从计算结果看，转向器越靠近L/2和支点，同等荷载作用下挠度越大，二次效应的不利影响也就越大。总体上看，转向器布置于距支点L/6～L/4时Pu的提升效果相对较好。

根据上述分析结果可知，设两个转向器时，转向器宜布置于距支点L/6～L/4位置处。

3.3 钢束转向角度θp

JTG/T J22-2008的8.3.1第4条规定，体外预应力钢束的张拉端或锚固端可设在梁底、梁顶或端横隔板根部，亦可将体外索的上锚固端布置在主梁端部腹板两侧。不同的张拉、锚固位置对应不同θp，明确θp对Pu的影响，对加固设计有一定指导作用。本文θp的参数设置及Pu的计算结果见表5，根据表中数据，绘制了Pu随θp的变化趋势见图7。

表5 θp的参数设置及Pu的计算结果Table5 ParameterssettingofθpandcalculatingresultsofPuθp/(°)Pu/kNσcon=0.10fpkσcon=0.15fpkσcon=0.20fpk10.0128.7141.9156.712.5132.3147.6163.915.0137.9155.1172.817.5145.1162.2168.820.0151.8157.4162.722.5146.1151.7157.625.0142.2148.3153.9

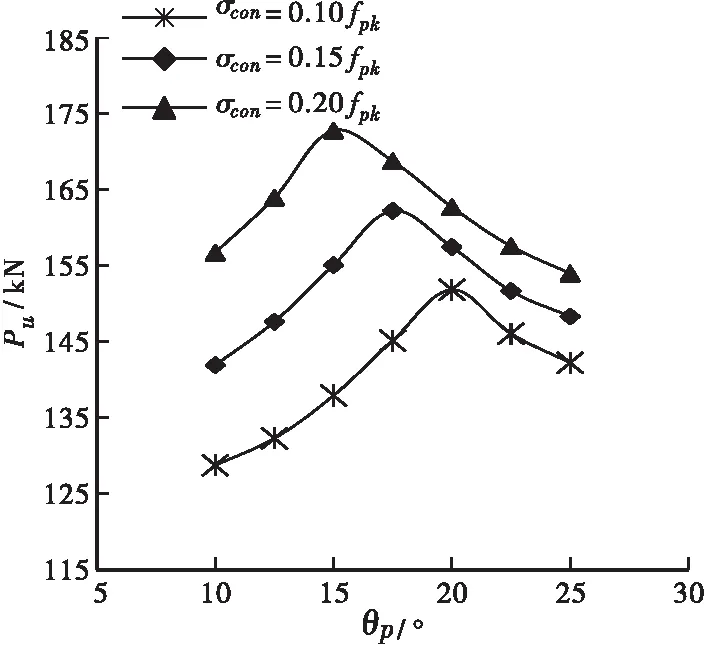
图7 Pu随θp的变化趋势

结合表5和图7可知：不同σcon下Pu随θp的变化趋势相同，Pu存在峰值点，θp过大、过小均不够理想，随着σcon增大，Pu峰值点对应的θp值在逐渐降低，说明σcon对θp有影响。原因是随着θp增大，同等荷载作用下Δp逐渐减小，二次效应的不利影响相应减弱，与此同时，体外预应力对梁体受拉区的预压效应也在逐渐减弱，表现为纵筋拉应力增长速度在逐渐变缓。二次效应对加固构件的受力不利，即为“负”作用，而体外预应力对梁体受拉区的预压效应对加固构件的受力有利，即为“正”作用，曲线峰值点对应的θp恰好为“正”、“负”作用效应综合对构件受力最有利时的钢束转向角度。在曲线峰值点左侧，二次效应的“负”作用较大，受拉区预压效应的“正”作用也较大，在曲线峰值点右侧，二次效应“负”作用减弱，但受拉区预压效应的“正”作用也在减弱，这两种情形均不够理想。随着σcon的增大，“正”、“负”作用效应综合对构件受力最有利时的θp在减小。

根据上述分析结果可知，当σcon较大时，θp取值不宜过大，σcon较小时，θp取值不宜过小。

3.4 钢束形心距梁侧面的距离Hd

Hd受横隔板配筋构造、锚固块及转向器尺寸等因素影响，对于加固设计时Hd如何合理取值，JTG/T J22-2008无明确规定或建议。本文Hd的参数设置及Pu的计算结果见表6，根据表中数据，绘制了Pu随Hd的变化趋势见图8。

表6 Hd的参数设置及Pu的计算结果Table6 ParameterssettingofHdandcalculatingresultsofPuHd/mmPu/kNHd/mmPu/kN20166.950116.725164.455106.530157.46096.135148.26583.540139.17072.445128.17558.6

图8 Pu随Hd的变化趋势

结合表6和图8可知：Pu随Hd增大而逐渐降低。对于两侧对称布束加固的直线简支梁，在理论上，Hd的大小对综合施加给主梁的预应力效应并无影响，即Hd不影响Pu。但计算结果表现与理论存在明显偏差，原因是锚固块的悬臂受力特点突出，随着Hd增大，悬臂根部破坏的可能性增大，加固构件的破坏模式逐渐发生转变，由正常的受弯梁破坏逐渐转变为非正常的锚固块区域梁体局部破坏，非正常的破坏模式并未体现加固构件的真实承载能力，体外预应力的加固作用也未得到有效发挥。下面以Hd=70 mm和Hd=20 mm的两个模型计算结果为例进行说明。①当Hd=70 mm时，达到Pu时，梁体第1主应力最大值σ1max位于端部锚固块位置，此时σ1max=2.1 MPa大于ft，梁体第3主应力绝对值最大值σ3max也位于端部锚固块位置，σ3max=13.8 MPa小于混凝土本构曲线峰值点及下降段所对应的应力值，受拉钢筋未屈服，钢束应力σp=322 MPa，结合Pu明显偏低的表现，说明Hd=70 mm时模型发生的是非正常的锚固块区域梁体局部破坏。②当Hd=20 mm时，荷载达到Pu时，梁体σ1max位于端部锚固块位置，σ1max=2.3 MPa大于ft，而梁体σ3max位于两加载点之间的受压区，σ3max=18.8 MPa位于混凝土本构曲线下降段对应的应力值，受拉钢筋屈服，钢束应力σp=542 MPa，结合Pu值的表现，说明Hd=20 mm时模型发生的是正常的受弯梁破坏。

根据上述分析结果可知，Hd取值宜小不宜大，Hd取值越大，钢束端部锚固区域发生提前失效的风险越大，体外预应力的加固作用越得不到有效发挥。

4 结论

本文采用有限元扩大参数分析方法，研究了体外预应力加固RC简支梁的钢束用量、转向器位置、钢束转向角度θp和钢束形心距梁侧面的距离Hd这4种加固参数对构件承载性能的影响，得出了以下结论：

a.随着钢束截面面积Ap的增大，构件在体外预应力加固下的极限承载力存在“回归值”，此“回归值”可用于确定最佳钢束用量。

b.设两个转向器时，转向器宜布置于距支点L/6～L/4位置处。

c.当张拉控制应力σcon较大时，θp取值不宜过大；σcon较小时，θp取值不宜过小。

d.Hd取值宜小不宜大，Hd取值越大，钢束端部锚固区域发生提前失效的风险越大，体外预应力的加固作用越得不到有效发挥。