半穿式钢桁梁桥上弦杆面外稳定性研究

程 高,张之恒,姬子田,刘小平

(1.长安大学 ,陕西 西安 710064；2.公路大型结构安全教育部工程研究中心,陕西 西安 710064；3.公路桥梁与隧道陕西省重点实验室,陕西 西安 710064；4.长庆工程设计有限公司,陕西 西安 710000)

0 引言

半穿式钢桁梁桥因桥面净空不受限且经济性好等优点而被广泛应用于中小跨径桁梁桥，然而半穿式钢桁梁桥上弦杆的面外稳定性问题一直是制约该桥型发展应用的关键因素，近年来得到了广泛的关注，1875年俄罗斯克夫达敞开式桥就因上弦杆受压失稳而引起全桥倒塌。因此，研究上弦杆的面外稳定性对半穿式钢桁梁桥的发展具有重要意义。

现有研究主要集中在半穿式钢桁梁桥的横向刚度。文献[1]对列车准高速通过半穿式钢桁梁桥的横向振动性能进行研究，以实桥为例证明了横向刚度能保证列车运行安全性。文献[2]理论分析了某实桥提速后横向振幅超限原因，提出了增大主桁下弦和下平纵联斜撑截面面积以增大横向刚度的方法。文献[3]根据轮轨摩擦与车辆横向振动性能的相关性原理，对润滑前后半穿式钢桁梁桥的横向振动进行对比分析，证明了轮轨润滑对横向拍波振动能起明显抑制作用。文献[4]提出了一种研究半穿式钢桁梁桥与列车系统空间振动的分析方法，采用计算机模拟，检算了刚度和运营平稳性。文献[5]通过有限元建模分析了半穿式钢桁梁桥的动力特性和横向振动，对比实测资料，提出了稳定性的合理加固措施。上述研究成果均说明了半穿式钢桁梁桥的横向刚度对上弦杆面外稳定性影响显著，为本文的研究奠定了基础。

本文在上述研究成果基础上，采用能量法，通过Maple数学计算软件给出了不同节间数下屈曲荷载的简化计算公式，该方法计算简便，与现有论文研究计算结果拟合良好，揭示了半穿式钢桁梁桥上弦杆面外稳定性的主要影响因素。以G211国道甘肃甜水桥为例，进一步分析了半穿式钢桁梁桥腹杆高度对上弦杆面外稳定性的影响，为半穿式钢桁梁桥腹杆设计提供了依据。

1 基于能量法的屈曲荷载分析

半穿式钢桁梁桥的端腹杆侧向支撑一般很强，将端腹杆对上弦杆的支撑作用等效为铰接边界条件。中间腹杆对上弦杆的支撑作用等效为弹簧，弹簧刚度为腹杆侧向支撑刚度。半穿式钢桁梁桥的上弦杆发生侧向屈曲时，根据受力状态，可简化为中间带弹簧支撑的简支梁计算模型如图1所示，图中上弦杆总长度为L,节间长度都为l,节间数为N，弹簧刚度为c，屈曲荷载为P，以左端点为原点，建立如图所示的直角坐标系。

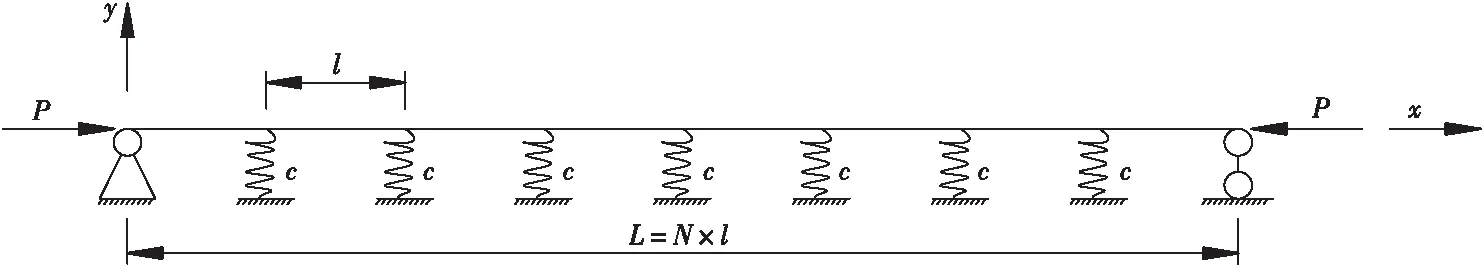
图1 简化力学模型

1.1 基本假定

为方便计算，半穿式钢桁梁桥上弦杆的简化力学模型满足如下假定：①端腹杆侧向刚度很大可简化为铰接；②中腹杆尺寸相同，每个弹簧刚度均相同；③上弦杆各节间长度相同；④上弦杆沿跨长方向为等截面；⑤上弦杆沿跨长方向轴力不变。

1.2 理论计算方法

半穿式钢桁梁桥横截面简化模型如图2所示，图中b为横梁长度；h为腹杆中心高度；Ib为横梁截面惯性矩；Ic为单榀桁架截面惯性矩。根据结构力学，双榀桁架侧向挠度Δ可表示为：

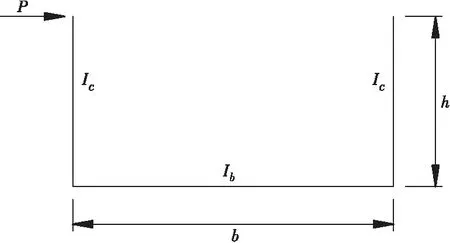
图2 横截面简化模型

(1)

弹簧刚度c是腹杆提供的侧向支撑刚度，与腹杆高度有很大关系，其数值为单榀桁架侧向挠度的倒数，弹簧刚度c可表示为：

(2)

为满足几何边界条件和静力边界条件，上弦杆屈曲时变形曲线可假设为：

(3)

式中：x为上弦杆顺桥向位置；y为上弦杆屈曲变形；n为形函数待定参数；B为形函数数量。

根据式(3)可以得到y对x的一阶导数和二阶导数：

(4)

(5)

上弦杆的弯曲应变能为：

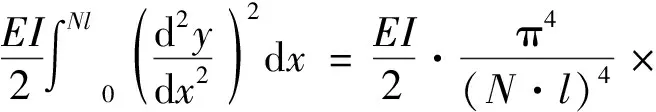
(6)

式中：I为上弦杆截面惯性矩。

弹簧位置的屈曲变形可表示为：

(7)

式中：k为屈曲变形待定参数。

上弦杆中弹簧应变能为：

(8)

外荷载所做的功：

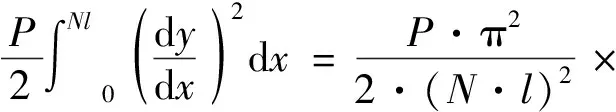
(9)

根据能量法，该结构的总能量为：

U=Ub+Ud-W

(10)

式中：U为结构总能量。

根据势能驻值原理，总势能的变分可表示为：

(11)

结构达到屈曲状态，由稳定的能量准则，应满足下式：

(12)

由式(12)可得n个线性齐次方程组，可用矩阵形式表达为下式：

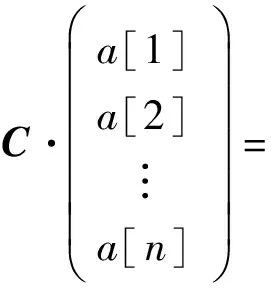
(13)

式中:矩阵D为稳定方程矩阵；矩阵C为方程组系数矩阵；结构达到屈曲状态；矩阵C对应的行列式应为0，可表示为式(14)：

(14)

由式(14)可得到屈曲荷载P。对于屈曲荷载P的求解，所取的形函数数量B越大，所得到的近似解越精确。根据计算方法可知当形函数数量B等于节间数N时，第N个方程所求得的荷载恰好为欧拉临界荷载Pcr，继续增加形函数数量对屈曲荷载P的影响已经很小。

1.3 简化计算公式

半穿式钢桁梁桥上弦杆节间数通常在4～12之间，不同节间数N对应的屈曲荷载P表达式有较大差别，采用上述理论计算方法，通过Maple数学计算软件，经大量编程计算，对不同上弦杆节间数的半穿式钢桁梁桥进行计算分析，提出了屈曲荷载P的简化计算公式如表1所示。从表1可看出弹簧刚度c对屈曲荷载P的影响很大，当弹簧刚度c较大时，对应的屈曲荷载P为单个杆件的欧拉临界荷载Pcr；当弹簧刚度c较小时，对应的屈曲荷载P计算式为含有多个参数的函数表达式。腹杆高度h是弹簧刚度c的主要影响因素，对半穿式钢桁梁桥上弦杆的面外稳定性具有重要意义。

表1 简化计算公式Table1 Simplifiedformulas节间数N弹簧刚度c屈曲荷载P4>63EIπ4256l3π2EIl24<63EIπ4256l381EIπ4+256cl3144π2l25>144EIπ4625l3π2EIl25<144EIπ4625l3256EIπ4+625cl3400π2l26>275EIπ41296l3π2EIl26<275EIπ41296l3625EIπ4+1296cl3900π2l27>117EIπ4600.25l3π2EIl27<117EIπ4600.25l3324EIπ4+600.25cl3441π2l28>735EIπ44096l3π2EIl28<735EIπ44096l32401EIπ4+4096cl33136π2l29>1088EIπ46561l3π2EIl29<1088EIπ46561l34096EIπ4+6561cl35184π2l210>144EIπ4625l3π2EIl210<144EIπ4625l3256EIπ4+625cl3400π2l211>1620EIπ47320.5l3π2EIl211<1620EIπ47320.5l36561EIπ4+14641cl39801π2l212>275EIπ41296l3π2EIl212<275EIπ41296l3625EIππ4+1296cl3900π2l2

2 算例及分析

2.1 甜水桥算例

以G211国道甘肃甜水桥为例，对半穿式钢桁梁桥上弦杆的面外稳定性进行计算。甜水桥为简支半穿式钢桁梁桥，主跨71 m，桁高5.95 m,桥宽14.8 m，高跨比为1/12，宽跨比为1/4.8，上弦杆节间数为8，节间长度为8 m，甜水桥立面布置图和横截面布置图如图3和图4所示。甜水桥上弦杆为圆形钢管混凝土，截面尺寸为φ1 000×24 mm，下弦杆为方钢管混凝土，截面尺寸为900 mm×900 mm×300 mm，腹杆为圆形空钢管，截面尺寸为φ630×26 mm，钢管采用Q390E钢材，管内混凝土采用C50自密实补偿收缩混凝土，杆件截面如图5所示。

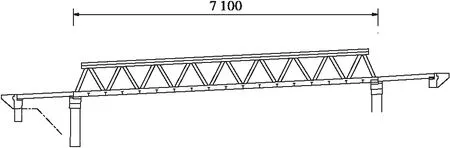
图3 甜水桥立面布置图(单位：cm)

图4 甜水桥横截面图(单位：mm)

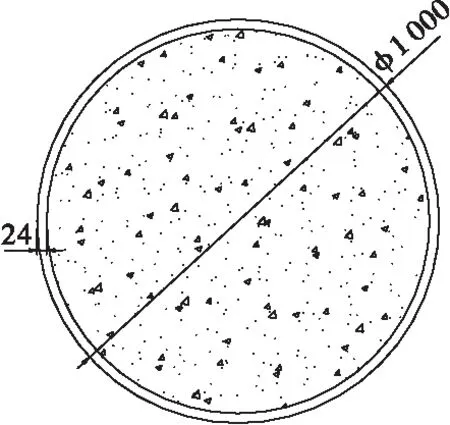
(a)上弦杆截面图

以甜水桥为例进行上弦杆面外稳定性计算，侧向支撑刚度可由式(2)计算，各抗弯刚度按照结构力学计算，得到结构参数如表2所示。

2.2 计算结果比较分析

半穿式钢桁梁桥上弦杆屈曲荷载P的现有计算方法如下：规范及书籍主要包括《铁路桥梁钢结构设计规范》(TB 10091-2017)[6]、《水运工程钢结构设计规范》(JTS 152-2012)[7]、《港口工程钢结构设计规范》(JTJ 283-99)[8]和《钢桥》(小西一郎)[9]中相关内容，规范及书籍都是引入计算长度的折减系数以考虑面外稳定性，通过查表可进一步计算屈曲荷载P。理论计算方法都较复杂，主要包括SHOU-NGO TU的差分法[10]和孙纲廷提出的计算方法[11]，如下所示：

表2 结构参数表Table2 StructuralParameters名称符号单位数值节间数N8节间长度lmm8000腹杆中心高度hmm5000横梁长度bmm13000钢材弹性模量EsMPa2.06·105混凝土弹性模量EcMPa3.45·104横梁截面惯性矩Ibmm42.7615·1011单榀桁架截面惯性矩Icmm43.58822·1012上弦杆截面惯性矩Imm41.552023·1010弹簧刚度cN/mm3443303.2472

SHOU-NGO TU通过差分法，提出屈曲荷载计算式：

(15)

其中，i为1到N的正整数;S为弹簧刚度参数;T为屈曲荷载参数。

孙纲廷采用能量法，提出屈曲荷载计算式:

(16)

其中，Q为1到N的正整数;S为弹簧刚度参数;T为屈曲荷载参数。

以甜水桥为例，对以上计算方法进行整理，计算结果如表3所示。从表3可看出，采用规范及书籍计算得到的屈曲荷载P都非常保守；本文基于能量法所得计算结果和SHOU-NGO TU差分法、孙纲廷计算法所得结果相同。

以甜水桥为例，其腹杆中心高度h和屈曲荷载P的关系如图6所示。从图6可看出，在一定范围内，屈曲荷载P随腹杆高度的增大而减少且影响显著，两者呈指数函数分布，当腹杆高度从4 000 mm降为2 000 mm，降幅为100%，对应的屈曲荷载P从947 585.6 kN升为2 675 742.6 kN,增幅约为182%。从图6还可看出，屈曲荷载P随腹杆高度增大而成为单个杆件的欧拉临界荷载Pcr，此临界荷载非常小，说明限制腹杆高度是提高半穿式钢桁梁桥上弦杆面外稳定性的有效途径，腹杆高度设计可参考本文提供的屈曲荷载P简化计算公式如表1所示。

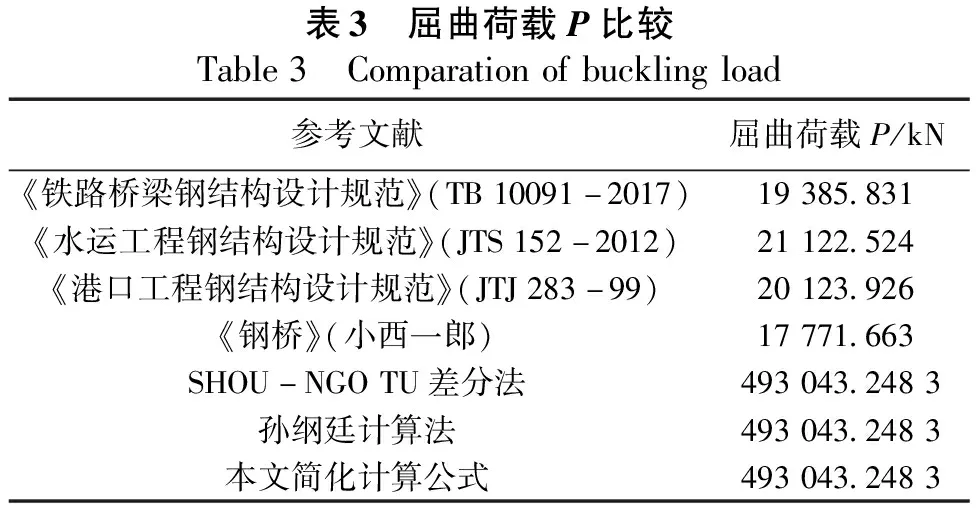
表3 屈曲荷载P比较Table3 Comparationofbucklingload参考文献屈曲荷载P/kN《铁路桥梁钢结构设计规范》(TB10091-2017)19385.831《水运工程钢结构设计规范》(JTS152-2012)21122.524《港口工程钢结构设计规范》(JTJ283-99)20123.926《钢桥》(小西一郎)17771.663SHOU-NGOTU差分法493043.2483孙纲廷计算法493043.2483本文简化计算公式493043.2483

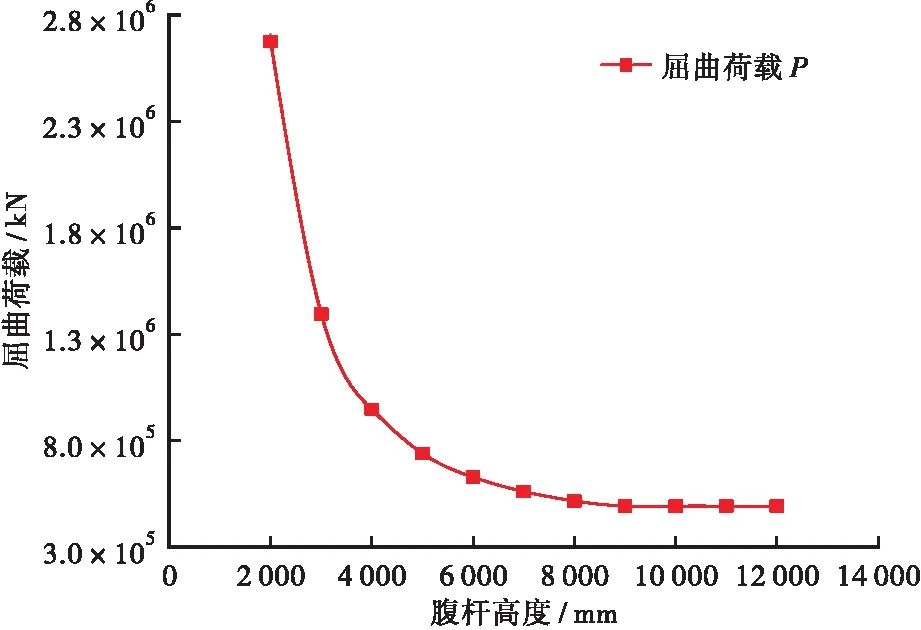
图6 腹杆高度和屈曲荷载P关系

3 结语

本文采用能量法，通过Maple数学计算软件对半穿式钢桁梁桥上弦杆的面外稳定性进行研究，提供了上弦杆屈曲荷载P的简化计算公式，结合G211国道甘肃甜水桥进行计算结果分析，可以得到如下结论：

a.半穿式钢桁梁桥上弦杆的面外稳定性主要和上弦杆抗弯刚度、侧向支撑刚度、节间长度和节间数有关。

b.不同节间数下上弦杆屈曲荷载的简化计算公式如表1所示。当弹簧刚度c较大时，对应的屈曲荷载P为欧拉临界荷载Pcr；当弹簧刚度c较小时，对应的屈曲荷载P计算式为含有多个参数的函数表达式。

c.以G211国道甘肃甜水桥为例，对现有屈曲荷载的计算方法进行比较，发现目前规范提供的计算方法非常保守；本文基于能量法所得简化计算结果与现有论文计算结果相同。

d.腹杆高度对半穿式钢桁梁桥的面外稳定性影响显著，通过限制腹杆高度可提高该类桥型的面外稳定性，本文提供的简化计算公式可用于指导半穿式钢桁梁桥的腹杆设计。