基于虚拟激励法的大跨径斜拉桥随机地震效应主塔力学响应特征

周孝飞,侍永生,雷顺成,李 谦

(1.湖南省交通科学研究院有限公司，湖南 长沙 410014；2.中交第二公路勘察设计研究院有限公司，湖北 武汉 430000)

斜拉桥由于其跨越能力大，结构美观，在我国桥梁建设中占据着重要地位。我国斜拉桥设计建造已经突破千米大关。对于大跨径斜拉桥，抗震设计显得尤为重要。目前，我国抗震设计规范主要适用于中小跨径桥梁或连续梁、连续刚构桥，对大跨径斜拉桥或悬索桥类柔性较大的结构的适应度不高，同时，当前主流抗震计算方法以反应谱法和时程分析法为主，反应谱法是一种静力等效法，且一般仅适用于结构线弹性工作状态，并且不能对结构内力响应过程进行定量描述，而时程分析法虽然能较为精确地追踪结构在地震效应下的力学响应过程，但是对地震波的适应度不高，仅适用于指定波形，两者均具有一定局限性[1-2]。而虚拟激励法作为一种等效处理方法，在结构支撑约束处施加无穷大质量块，通过求解约束位置的绝对位移，经换算即可获得实际地震加速度解析解，此法可有效解决有限元分析时地震实际加速度模拟困难的问题，从而获得较为精确的结构力学响应特征。

在以往斜拉桥抗震研究中，研究人员主要研究方向为主梁、索梁及索塔锚固区域的响应规律，而关于主塔研究较少，相关力学特征和受力机理难以明确，从而为斜拉桥抗震设计带来很多困难。本文以某大跨径斜拉桥为工程背景，建立ANSYS有限元模型，运用虚拟激励法探讨斜拉桥主塔在多维多点随机地震激励下受力规律，明确行波效应、相干效应、局部场地效应对主塔力学性能的影响。该研究成果可为大跨径斜拉桥抗震设计及计算提供一定参考。

1 虚拟激励法计算方法及功率谱函数

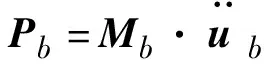
(1)

式中：第1项表示惯性力矩阵；第2项表示阻力矩阵；第3项表示弹性力矩阵；s和b分别为非支撑节点和支撑节点；Pb为3个方向的地震力矩阵向量；Xs为节点位移向量；Xb为地面强迫位移向量。

(2)

(3)

式(3)可理解为：当在结构支撑位置处施加一质量无穷大的质量块时，结构在支撑位置处的加速度响应值等于地震实际加速度值，在有限元模型中的各支撑节点上施加大质量，即可在ANSYS软件中实现地震加速度的输入，该法可巧妙解决ANSYS中地震加速度难以模拟的问题[5]。

使用虚拟激励法模拟随机地震效应时，应选取合适的功率谱参数模型及相关计算参数。研究表明：在稳态随机地震效应下，其加速度场功率谱可通过式(4)表示。

S(iω)=

(4)

式中：Snn(iω)表示各支点自功率谱密度函数:Skl(iω)是互功率谱密度函数，其具体形式见式(5)。

ρkl(iω)=|ρkl(iω)|exp(-iωdkl/vapp)

(5)

式中：|ρkl(iω)|表示相干函数ρkl(iω)，以反映部分相干效应；exp(-iωdkl/vapp)表示ρkl(iω)幅角，以体现行波效应，vapp为地震波的视波速。

根据二项式定理将加速度功率谱矩阵展开，可得到考虑各方向的加速度分量的相干程度表达式。

Sxx(iω)=Syy(iω)=Sxy(iω)=Syx(iω)

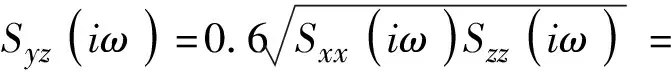
(6)

联合式(4)～式(6)，即可求得随机地震多维多点激励的功率谱曲线函数。

2 工程概况

以湖南南益高速公路上胜天大桥为工程背景，该桥结构形式为双塔双索面钢箱梁斜拉桥，是南益高速公路上控制性工程，整桥采用半漂浮体系，桥跨组合为(181.9+450+181.9)m，设计荷载等级为公路—I级。主梁截面形式为正交异性桥面板钢箱梁，主桥全宽30.5 m。全桥共有68对扣索，每个主塔两侧分别布置17对扣索，斜拉索索间标准间距为12 m，索塔及索梁加密区扣索间距为5 m，斜拉索与索塔之间通过钢锚箱锚固，与主梁之间约束采用锚板的形式，斜拉索采用抗拉强度为1 770 MPa的预应力钢绞线。在过渡墩位置设置竖向活动支座，支座约束为释放顺桥向约束，钢箱梁采用分段吊装焊接施工[6]。桥型布置图及横截面布置图如图1和图2所示。

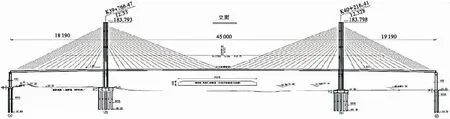
图1 胜天大桥桥型布置图(单位：cm)

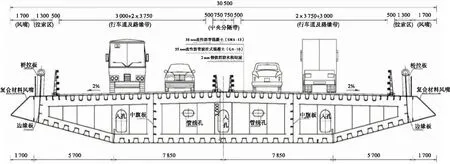
图2 胜天大桥标准钢箱梁节段截面示意图(单位：mm)

3 有限元模型建立

钢箱梁斜拉桥属于典型空间受力结构。使用Beam188三维空间梁单元实现对主梁的模拟，为简化计算，不考虑箱梁畸变、剪力滞等局部效应的影响，通过MPC184单元将横梁等效为刚性梁，不计入横梁重量，采用集中质量法将主梁质量平均分配到纵梁上。斜拉索采用Link10杆单元模拟，并激活仅受拉特性，通过Enrst公式对弹性模量进行修正，斜拉索索力以初应变的形式输入，主塔使用Solid45三维实体单元模拟，主塔与扣索之间共节点，忽略钢锚箱的约束作用。有限元模型如图3所示。

图3 ANSYS有限元模型示意图

根据前节确定的虚拟激励模拟方法，在斜拉桥支撑位置施加无穷大质量块即可实现对地震加速度的等效模拟。本文通过在支撑约束位置布置Mass21质量单元，并施加109kN重力，实现对无穷大质量块的模拟。

4 随机地震模型参数确定

首先对结构自振频率进行计算，考虑结构大变形初始应力状态，基于Block Lanczos法对结构自振特性进行求解，获取结构前100阶振动频率及振型。因篇幅限制，本文给出结构前10阶自振频率及振型计算结果。

表1 胜天大桥前10阶频率及振型Table1 Thefirst10frequenciesandvibrationmodesofShengtianBridge阶数振动频率/Hz振型描述10.149主梁一阶纵飘20.268主梁一阶竖弯(正对称)30.339主梁一阶横弯(正对称)40.347主梁一阶竖弯(反对称)50.602主梁二阶竖弯(正对称)60.674主塔一阶横弯(反对称)70.679主塔一阶横弯(正对称)80.702主梁二阶竖弯(反对称)90.793主梁三阶竖弯(正对称)100.911主梁一阶横弯(反对称)

(a)一阶振型

根据桥梁振动特性计算结果可知，由于该桥采用半漂浮结构体系，故结构振动频率较小，一阶振型为主梁纵飘，这是因为采用全漂浮体系或半漂浮体系的斜拉桥，主梁纵飘往往是低阶振型，对结构主梁纵向地震响应有显著贡献，二三阶振型分别为一阶竖弯和一阶横弯，对应控制量分别为地震效应下顺桥向弯矩和横桥向弯矩。需要指出的是，在前十阶频率中，主塔模态出现较早，且均为横弯，说明主塔抗弯能力不足，横向刚度有待加强。

由于半漂浮体系的柔性特质，胜天大桥前10阶自振频率较小，且低频成分复杂，极易出现某集中模态耦合作用导致的相互干扰，给结构分析带来困难。为克服低频成分相互干扰导致的收敛困难的问题，本文选用杜修力-陈厚群模型作为随机地震输入模型，该模型可解决其他模型在低频处理时的缺陷，能够较为精确地反映地震波的频谱特性，适用于频率较低的大跨度桥梁地震分析，杜修力平稳随机地震加速度模型表达式见式(7)。

(7)

式中：ωg、ξg分别表示场地土卓越频率和阻尼比；D表示加速度脉冲宽度；ω0为低频频率；S0为初始震源函数谱。

根据大桥地震地质勘察设计资料及杜修力模型参数确定方法[7]，初步拟定以下参数作为输入参数：S0=17.26 cm2/s3；D=0.011 4；ω0=1.83;ωg=13.03；ξg=0.03；X、Y、Z这3个方向加速度比值取为1∶0.85∶0.65，功率谱密度比为1∶0.722 5∶0.422 5，将各参数输入至杜修力模型中，根据式(4)～式(6)，经二项式展开后，在Matlab中求解功率谱函数矩阵，从而得到3个方向上加速度功率谱密度，即：sox=17.26 cm2/s3；soy=14.671 cm2/s3；soz=11.219 cm2/s3。功率谱密度曲线见图(5)。

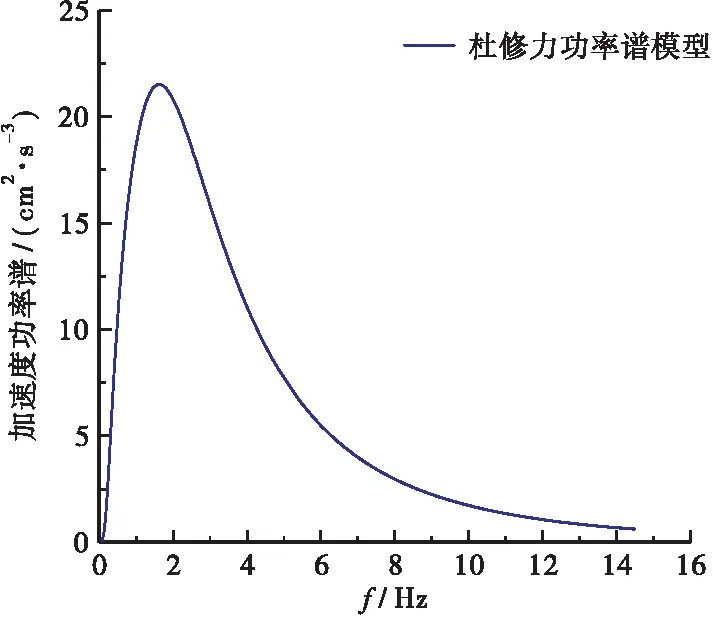
图5 杜修力模型功率谱密度曲线

5 随机地震下斜拉桥主塔空间效应力学响应特征

根据确定的杜修力模型输入参数及上述章节中关于在ANSYS中随机地震虚拟激励的实现方法，将功率谱密度函数输入至斜拉桥各约束支撑位置的质量单元上，通过求解约束位置绝对位移的方法获取随机地震加速度值，从而得到斜拉桥主塔在随机地震下的受力特性及规律。同时，在大跨径桥梁抗震分析中，空间效应的影响不容忽视，在进行随机地震的空间效应分析时，应考虑行波效应、相干效应和局部场地效应的影响。

5.1 行波效应主塔力学行为

行波效应对结构力学响应特征有较大影响，特别是对于高次超静定结构，行波效应的影响不容忽视[8]。本文采用SMART-1台阵43记录的地震波数据拟合公式[8]，见式(8)，同时选取行波效应下v=1 000 m/s和v=4 000 m/s两种常量视波速和一致激励(v=∞)进行对比，分析行波效应对主塔受力的影响。

(8)

式中：c1、c2均为拟合参数，根据台阵参数拟合结果，43号地震波，c1、c2分别取值3 654、1 105。

图6～图10给出了胜天大桥在行波效应、常量视波速以及一致激励下索塔内力及顺桥向位移响应结果，对比分析结果表明：在行波效应影响下。索塔沿顺桥向弯矩呈减小趋势，但幅度不大，沿塔高方向变化规律则基本一致；但索塔根部剪力和轴力有大幅增长，由两种常量视波速结果可知，其变化幅度与视波速变化不成正比；同时，索塔顺桥向位移随视波速增大呈减小趋势。对比一致激励法的计算结果，行波效应对索塔内力及位移响应的影响较为复杂，不是简单的线性增大或减小的关系，呈现出典型的耦合特性，同时，行波效应的影响受视波速影响较大，在视波速较低时，索塔响应随波速增加而减小；当波速无穷大时，索塔响应则等同于一致激励。

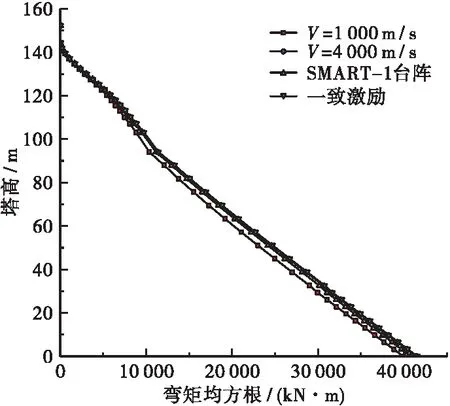
图6 索塔弯矩均方根(Ⅰ)

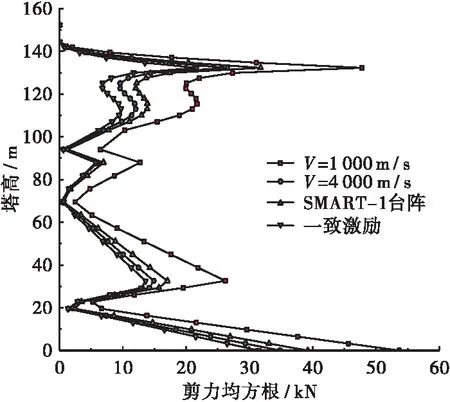
图7 索塔剪力均方根(Ⅰ)

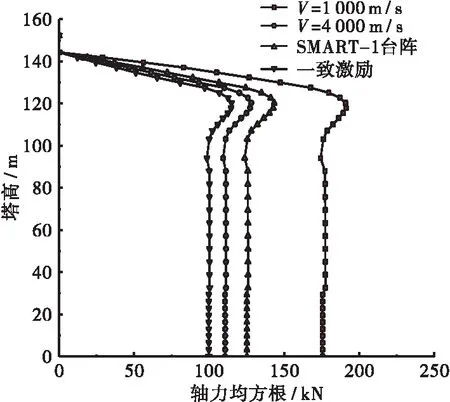
图8 索塔轴力均方根(Ⅰ)

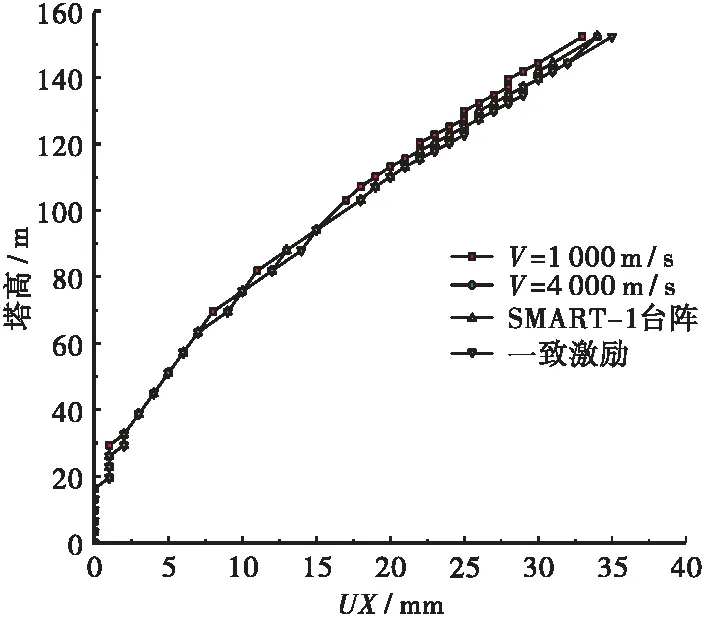
图9 索塔顺桥向位移均方根(Ⅰ)

5.2 相干效应主塔力学行为

在地震波传播过程中，受地层介质或其他因素的影响，会发生散射、折射、衍射等，这种效应被称为相干效应。相干效应可分为完全相干效应、部分相干效应和不相干效应这3种情况。本文拟选取QWW模型来描述相干效应的影响，其数学表达式见式(9)。

(9)

式中：α(ω)=α1ω2+α2，a1=0.000 016 78，a2=0.001 219;b(ω)=b1ω2+bα2，b1=-0.005 5，b2=0.767 4。

将QWW模型输入至ANSYS有限元模型中，获取斜拉桥主塔弯矩、剪力、轴力及顺桥向位移响应值，见图10～图13所示。对比分析结果表明：完全相干时，主塔弯矩及位移响应与一致激励时一致，部分相干和不相干效应对主塔受力影响的规律大致相同，仅程度有所区别。相干效应下，主塔弯矩、剪力及位移有一定幅度减小，轴力则有较大幅度增大，考虑到索塔主要由弯矩控制，可认为相干效应在一定程度上对索塔随机地震下力学响应是有利的。

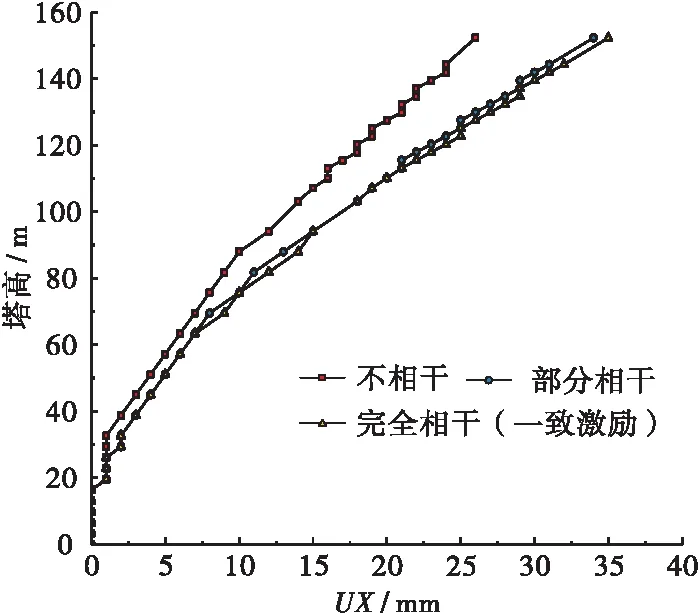
图13 索塔顺桥向位移均方根(Ⅱ)

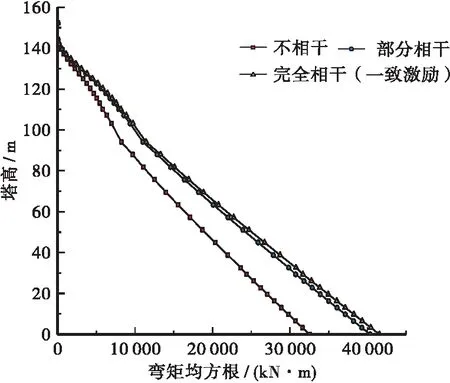
图10 索塔弯矩均方根(Ⅱ)

5.3 局部场地效应主塔力学行为

在大跨径桥梁抗震分析时，存在结构支撑点之间的场地差异引起内力响应变化的情况，因此，局部场地效应不容忽略。本文采用屈铁军半经验公式，对比分析局部场地效应和一致激励下斜拉桥主塔内力及位移响应特征。根据设计资料，取土层厚度变化差值Δh=5 m，震中距离差值取过渡墩间距Δx=632 m。

ΔS0=0.257 1Δh-0.012 4Δx

(10)

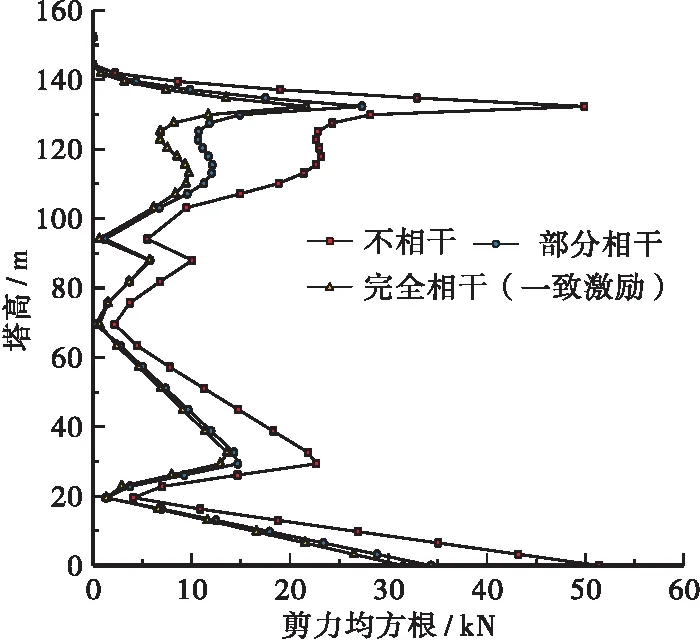
图11 索塔剪力均方根(Ⅱ)

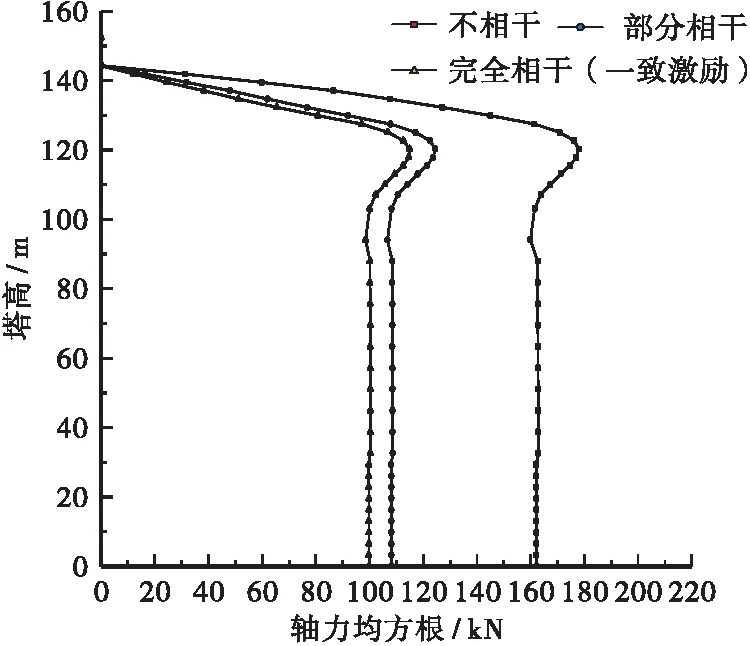
图12 索塔轴力均方根(Ⅱ)

式中:ΔS0表示自功率谱差值；Δh表示土层覆盖厚度差值；Δx表示震中距离差值。

图14～图17给出了局部场地效应与一致激励效应下主塔弯矩、剪力、轴力及顺桥向位移均方根对比结果，计算结果表明，考虑局部场地效应后，主塔内力及位移均有大幅增加，尤其是索塔根部弯矩值，增幅在50%左右，这对于以弯矩作为控制指标的主塔而言是极为不利的。在设计时应充分考虑局部场地效应对主塔弯矩的影响，且由式(10)可知，覆盖土层厚度对场地效应的影响远大于震中距差，在桥梁选址时应尽可能避开覆盖土层厚度差值较大的位置。

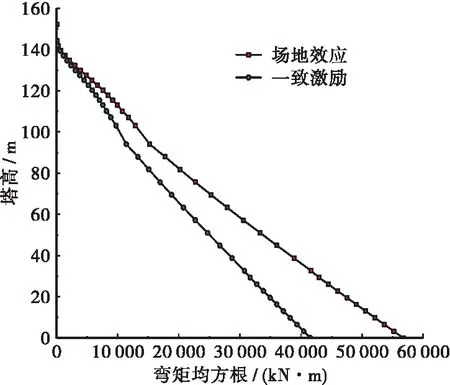
图14 索塔弯矩均方根(Ⅲ)

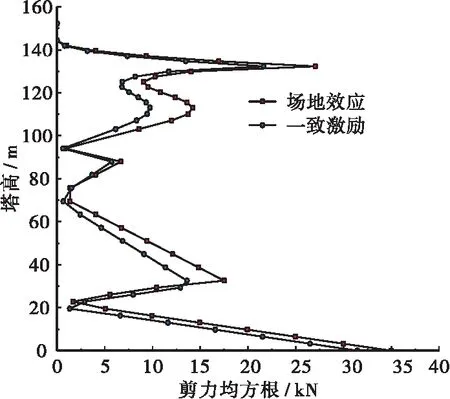
图15 索塔剪力均方根(Ⅲ)

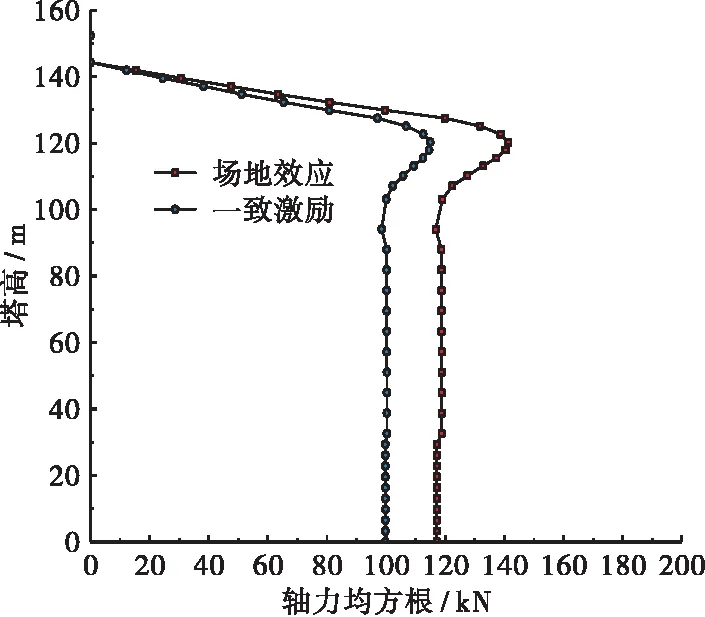
图16 索塔轴力均方根(Ⅲ)

图17 索塔顺桥向位移均方根(Ⅲ)

6 结论

以某大跨径钢箱梁斜拉桥为研究对象，建立该桥ANSYS有限元模型，运用虚拟激励法分析了随即地震下斜拉桥主塔的空间效应，可得到以下结论：

a.行波效应对主塔受力影响复杂，呈现典型的耦合特性，在行波效应下，索塔根部弯矩有小幅降低，但控制截面剪力和轴力有一定增长。行波效应受视波速大小影响显著，视波速越小，索塔响应越剧烈，结构受力越偏不利。

b.在QWW相干模型下，索塔力学响应与相干程度有关，但规律大致相同。索塔顺桥向弯矩、剪力、位移有一定程度减小，轴力大幅增加，考虑到索塔主要由受弯控制，因此可认为相干效应对索塔受力是有利的。

c.局部场地效应对索塔内力有放大效应，采用屈铁军半经验公式时，索塔根部弯矩最大增幅可达50%左右，局部场地效应主要受覆盖土层厚度差有关，厚度差越大，内力响应越剧烈。