初中数学教材解读两例
摘要:当下,一些数学教师的教学脱离了教材,没有深度理解教材编写的意图。针对有关湘教版初中数学七年级上册的两个教学案例,剖析其对教材解读的不足,发现教材的编写有时能够帮助学生更好地理解知识,有时给了教师尽情展示自我的平台。
关键词:教材解读;教学诊断;多个有理数相乘;有理数的减法法则
教材是众多专家的智慧结晶,是教师教学的重要依据和参考。教师教学首先要读懂教材。但当下,一些数学教师的教学脱离了教材,没有深度理解教材编写的意图。下面,给出有关湘教版初中数学七年级上册的两个教学案例,剖析其对教材解读的不足。
一、“多个有理数相乘”为什么放在“有理乘法的运算律”这一小节?
湘教版初中数学教材没有将“多个有理数相乘”放在“有理数的乘法(法则)”这一小节,而将其放在之后的“有理数乘法的运算律”这一小节。
笔者调研发现,一些教师教学“有理数的乘法法则”时,会在“两个有理数相乘”的内容之后,拓展、拔高至“三个及以上有理数相乘”(即“多个有理数相乘”)的内容。对此,他们的解释是:加大“课堂密度”,提升思维深度。
但是,道理真的就这么简单吗?教材为什么要这么处理?
确实,表面看来,从两个有理数相乘到多个有理数相乘,因数的数量由少到多,计算的长度由短到长,思维的层次由简单到复杂,知识在“最近发展区”内递进,体现了课堂教学的自然深入。
但是,从前后知识关联的角度看,乘法交换律、乘法结合律、乘法对加法的分配律正是在多个因数相乘的环境中才“大显身手”的。也就是说,多个因数相乘如果按乘法法则(实质是两个有理数相乘的法则)计算,就是按自然顺序求解,则会显得烦琐(比如多次定符号、多次求绝对值及其积),从而引起指向“简化”的思考,即得出对认识乘法交换律、结合律、乘法对加法的分配律的必要性和重要性的追求。换句话说,把“多个有理数相乘”和“乘法运算律”放在一起教学,既是对乘法法则理解的加深,更是对乘法运算律的价值(简化多个有理数相乘的运算)理解的加深。
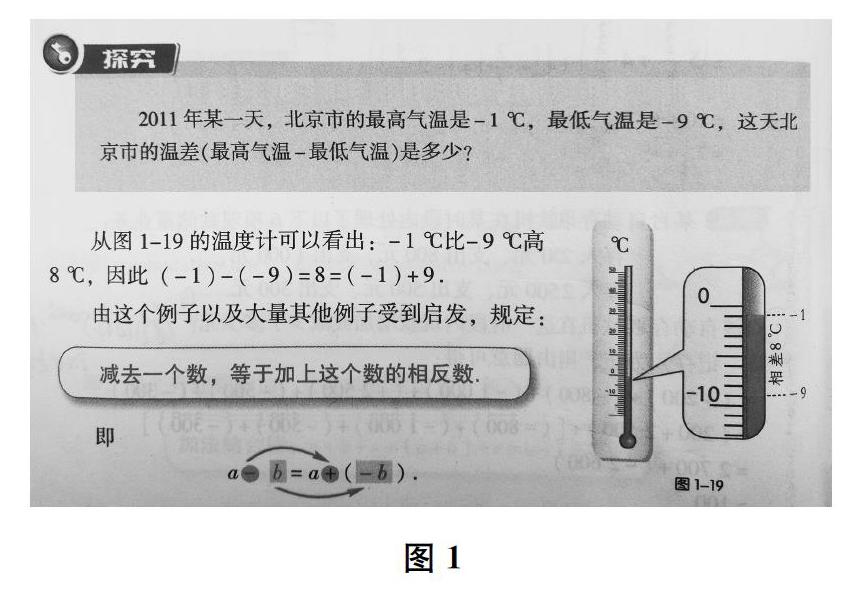
二、有理数的减法法则为什么利用温度计情境揭示?
湘教版初中数学教材中,有理数的减法法则是结合温度计情境,通过“由这个例子及大量其他例子受到启发,规定:减去一个数,等于加上这个数的相反数”这句话揭示的(见图1)。
笔者调研发现,一些教师教学“有理数的减法法则”时,要么就这个例子,一次举例得出法则;要么另起锅灶,运用加法[如8+(-9)=-1]改写算式[如-1-(-9)=8或-1-8=-9]的大量例子来揭示法则。
但是,这个温度计情境真的可有可无吗?其直观价值就这么肤浅吗?
首先,必须说明一个基本观点:生活中大多是“观察直觉”确认,数学上通常是“演绎推理”确认,而数学教学处于“中间地带”,有很多的发挥空间。因此,教材实际上在用“由这个例子及大量其他例子受到启发,规定……”这句并不简单的话来暗示、鼓励教师借助温度计情境展开“同课异构”“创新设计”,帮助学生充分理解有理数的减法法则。比如,可以这样设计教学:
第一环节,观察一个温度计,确认:零上8℃是基于标准“零度”读出来的,用生活语言表达就是8℃比0℃高8℃,用数学式子表达就是8-0=8;显然,0℃比0℃高0℃,即0-0=0;零下8℃是基于标准“零度”读出来的,用生活语言表达就是零下8℃比0℃低8℃,由负数的意义用数学符号表达就是-8℃比0℃高-8℃,用数学式子表达就是-8-0=-8。把三个数学式子放在一起,可归纳得出“一个有理数减去零仍得这个有理数”。
第二环节,观察两个温度计,其中一个显示甲地某一天温度是零下1℃,另一个显示乙地同一天温度是零下9℃,确认它们的温度差是8℃,列出数学式子-1-(-9)=8;假设两地第二天温度都升高了9℃,确认它们的温度差没有变化,列出数学式子(-1+9)-(-9+9)=-1-(-9);结合“互为相反数的两数和为零”和上述结论,可得(-1+9)-(-9+9)=(-1+9)-0=-1+9。综合后面两个数学式子,可得-1-(-9)=-1+9。由此,可以归纳得出有理数的减法法则。
综上,教材的编写有时能够帮助学生更好地理解知识,是“深度学习”的良好范例,比如上述第一个案例;有时给了教师尽情展示自我的平台,是“二次开发”的良好载体,比如上述第二個案例。
由此,可以进一步得到教材解读及其教学的启示:一方面关注数学的知识结构及思想方法,尝试用一些“大概念”或“高观点”,从不同的角度重新组织(“重构”)知识内容,促进学生的知识理解;另一方面挖掘学习素材的价值,充分引导学生“用数学的眼光观察世界,用数学的思维思考世界,用数学语言表达世界”,感悟数学知识的含义与价值。
参考文献:
[1] 陈金红.你真的看过教材?[J].湖南教育(下),2014(12).

