数学教学中渗透劳动教育的路径探析

孔繁晶

摘要：将劳动教育融入学科教学，是劳动教育最终落地的一条重要途径。在数学教学中渗透劳动教育的路径有：关注数学文化，联系生产生活，结合学科精髓，树立劳动观念;开展数学实践，重视数学建模，体验劳动创造。

关键词：数学教学;劳动教育;劳动观念;劳动创造

2018年9月，习近平总书记在全国教育大会上的讲话指出：“要在学生中弘扬劳动精神，教育引导学生崇尚劳动、尊重劳动，懂得劳动最光荣、勞动最崇高、劳动最伟大、劳动最美丽的道理，长大后能够辛勤劳动、诚实劳动、创造性劳动。”这段重要的论述将劳动教育的地位和意义提到了前所未有的高度，丰富了新时代劳动教育的内涵和外延。新时代的教育必须充分重视劳动教育，真正实现德智体美劳“五育”并举，才能落实立德树人的根本任务。

2020年3月，中共中央、国务院发布的《关于全面加强新时代大中小学劳动教育的意见》进一步要求：“除劳动教育必修课程外，其他课程结合学科、专业特点，有机融入劳动教育内容。”由此可见，将劳动教育融入学科教学是劳动教育最终落地的一条重要途径。数学课程作为高中学段主干课程之一，如何在教学中找到渗透劳动教育的切入点，通过怎样的路径实现智育与劳育并举的效果，成为当前教师需要探析的新课题。下面，笔者结合自己的教学与思考浅谈一二。

一、树立劳动观念

劳动教育的关键在于帮助学生树立正确的劳动观念，端正劳动态度。数学作为一门有着几千年历史积淀，又历久弥新，不断散发着魅力的学科，具备丰富的劳动观念因子。教师需潜心关注，有机渗透。

（一）关注数学文化

数学源自生产生活，也就是源自劳动。结绳记事、算筹计数等是人类在探索劳动过程中产生的方法，《几何原本》《九章算术》等是人类在记录劳动经验中总结的成果。因此，教师在数学教学中应充分关注数学起源、发展的人类文化，挖掘其中的劳动教育资源，引导学生体会劳动价值。

例如，教学苏教版高中数学教材“直线与平面垂直”时，教师充分挖掘教材课后习题的文化内涵，引入鳖臑模型，从文化传承的角度引导学生认识劳动价值，形成正确的劳动观念。

首先，教师引导学生解决教材习题：如图1，AB是圆O的直径，PA垂直于圆O所在的平面，C是圆O上不同于A、B的任一点，求证：BC⊥平面PAC。

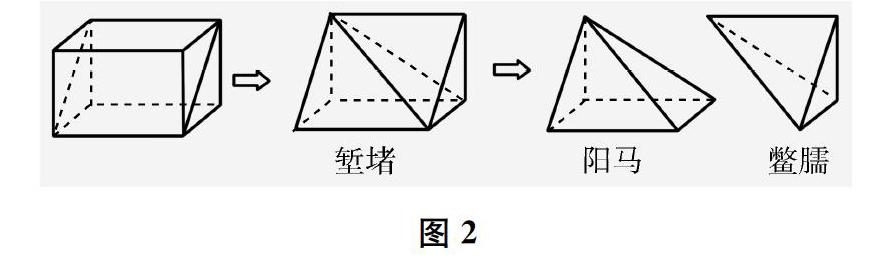
其次，教师介绍鳖臑及其由来：“同学们请注意，题目中的三棱锥可是大有来头。这个四个面均为直角三角形的三棱锥叫作鳖臑。追溯起来，它是我国古代劳动人民在筑城、筑墙、挖沟、挖渠、建仓、建屯等工程中总结出的一组特殊模型之一，被收录在《九章算术》中。”接着，教师出示《九章算术·商功》中的原文：“斜解立方，得两堑堵。斜解堑堵，其一为阳马，一为鳖臑。”并出示图2，解释：“用现代汉语讲就是，取一个长方体，斜割一分为二，得到两个一模一样的三棱柱，称为堑堵。再沿堑堵的一个顶点与相对的棱剖开，得到一个四棱锥和一个三棱锥。四棱锥叫作阳马，三棱锥叫作鳖臑。”

再次，教师引导学生研究阳马和鳖臑的性质：（1）制作模型，平面展开，探究阳马和鳖臑各个面的形状及关系;（2）分别研究阳马和鳖臑中的各种垂直关系;（3）将阳马和鳖臑放在一起，探究其相互关系;（4）你们还发现了什么？

最后，教师总结：“这两个立体几何模型太厉害了！它们蕴含丰富的空间关系，涵盖多面体的所有要素，是立体几何中不可多得的研究对象。它们就是中国古代劳动人民在长期的劳作中凝结出的智慧。所以，同学们必须明白，劳动是创造一切文明的源泉。”

（二）联系生产生活

生产生活是数学的起点，也是数学的归宿。远到游牧、农耕文明的兴起，近到大数据时代的空前发展，大到天文、航海，小到买菜、贴砖，皆体现着数学的应用价值。究其本质，在于数学的应用提升了劳动实践的水平。但“唯应试”的数学教学往往追求“短平快”，实施“掐头去尾烧中段”，使学生误认为数学是脱离生产生活的“空中楼阁”。因此，教师应将数学教学植根于生产生活，引入建筑、工程、当代统计等领域有关劳动的实例，帮助学生建立劳动意识。

例如，高三复习教学中，教师可以引导学生解决如下高考试题：

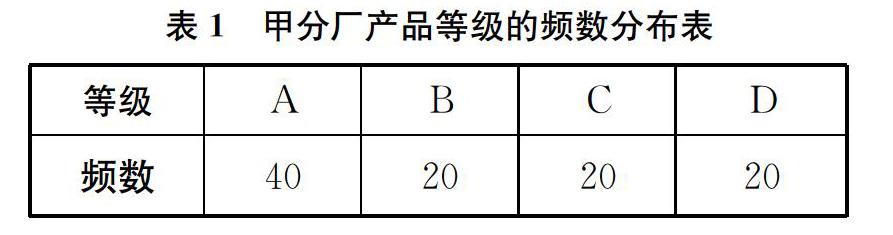
某厂接受了一项加工业务，加工出来的产品（单位：件）按标准分为A、B、C、D四个等级。加工业务约定：对于A级品、B级品、C级品，厂家每件分别收取加工费90元、50元、20元;对于D级品，厂家每件要赔偿原料损失费50元。该厂有甲、乙两个分厂可承接加工业务。甲分厂加工成本费为25元/件，乙分厂加工成本费为20元/件。为了决定由哪个分厂承接加工业务，厂家在两个分厂各试加工了100件这种产品，并统计了这些产品的等级，整理如表1、表2所示。

（1）分别估计甲、乙两分厂加工出来的一件产品为A级品的概率;

（2）分别求甲、乙两分厂加工出来的100件产品的平均利润，以平均利润为依据，厂家应选哪个分厂承接加工业务？

本题融合当代劳动元素，以工厂的生产质量管理为背景，考查古典概型概率公式的应用，以及平均数的求法。教师要抓住契机引导学生作出决策，建立劳动意识：“我们看到，数学源于生产生活，又指导生产生活。数学的价值在于提升劳动实践的水平。我们只有不断追求高质量的劳动成果，才能实现劳动致富。”

（三）结合学科精髓

数学的起源、发展伴随着一路坎坷、诸多波折。其中，数学家严谨、坚毅的品质正是劳动精神的体现。而数学学科的学习要通过信息整合、思考探究、实践证明等，最终提升抽象、推理、直观、运算等素养。这一过程同样伴随着高强度的脑力劳动与体力劳动。也可以说，数学学习是一场劳动训练。所以，无论从学科特点还是从学科学习特征看，数学精神都与劳动精神十分契合。因此，教师在数学教学过程中应有机渗透这一观念，引导学生秉承劳动精神，攻坚克难，完成数学学习;并在数学学习过程中，倡导踏实奋斗、百折不挠，滋养劳动精神。

例如，“随机事件的概率”教学片段——

（教师介绍历史上著名的重复抛掷硬币试验，出示表3。）

师历史上许多统计学家都做过大量的抛掷硬币试验，抛掷硬币本质上就是制造一个极简的随机数生成器。那么，从试验结果中你发现了什么？

生从表中数据发现：当试验次数很多时，正面朝上的频率接近于常数0.5，并在其附近摆动。

师同学们注意一下这些统计学家试验的次数。德·摩根、布丰几千次，费勒、皮尔逊、罗曼诺夫斯基几万次，看到这样的数据大家有什么感受？

生这些统计学家的研究成果固然重要，但他们的科学精神也很重要，他们真的付出了大量的劳动。

生尤其是在不知道结果的情况下依然坚持。

生其实，这种精神也是我们在学习和生活中要汲取的。

师是的。所有的探索都是一场未知结果的劳动，但是科学家们不畏风雨、不惧挫折。千百年来，我们就是这样通过劳动实践一点一点靠近真理的。这是劳动精神，也是我们所追求的数学精神。

二、体验劳动创造

创造性劳动是习近平新时代中国特色社会主义劳动思想的核心理念，其要义在于创新。而数学学科的特点之一也是创新，数学学习更需要让学生“再创造”。数学不仅具备丰富的劳动观念因子，而且包含丰富的劳动实践载体。所以，教师在数学教学中要给学生创造劳动实践的機会，引导学生体验劳动创造。

（一）开展数学实践

《普通高中数学课程标准（2017年版）》将“双基”调整为“四基”，并首次提出要关注学生的“数学基本活动经验”，包括“思维的经验”和“实践的经验”，强调亲身体验、感悟。因此，教师在数学教学中要有意识地引导学生在多样化的实践活动中锻炼劳动技能，同时提升思维品质。

例如，教学《椭圆概念》一课。课前，让学生3—4人一组模仿工匠师傅利用“两点一线”绘制椭圆的方法，自制设备绘制椭圆，并拍摄视频。课上，请学生代表播放视频，然后讨论——

师同学们，你能用语言来描述你们组的操作方法吗？

生我们在硬纸板上固定两个钉，然后将一根绳子的两端固定在两个钉子上，拉直绳子转一圈就能得到一个椭圆。

师嗯。那有什么要注意的地方吗？

生绳子要比两个钉子之间的距离长。

师详细说说。

生刚开始没注意，绳子截短了，后来想了一下，必须比两个钉子之间的距离长，短或者一样长都不行。

生我们还发现，绳子越短，椭圆越扁。

师是将两个钉子固定的情况？

生嗯。

师两个变量固定一个，非常好！这就是我们研究问题常用的手段。

生那也可以固定绳长？

生对。我们试试。

（学生再次动手操作。）

……

（课尾，播放用椭圆规绘制椭圆的视频。）

师生活中，工匠师傅绘制椭圆还常常用到一个法宝，那就是椭圆规。请大家课后结合视频，分析其数学原理，并尝试用其绘制椭圆。

课前活动让学生模仿工匠劳动，亲自体验，在这个过程中，发现椭圆定义中的要点所在，即两定点（距离为2c）、一定长（为2a）以及2a>2c，升华得出真知;并且，引发创造性探索，即关注a或c的变化对椭圆形状的影响，为后续学习提供良好的素材。课后活动引导学生理论联系实际，从中再一次挖掘数学原理，进一步巩固所学，并主动拓展。

（二）重视数学建模

数学建模是指利用数学知识构建数学模型，创造性地解决实际问题，比纯粹的数学应用综合性、应用性以及创新性更强。而在建模解模的过程中，学生可以操作劳动工具，体验劳动过程，在体力劳动中激发脑力劳动，并以脑力劳动的成果提升体力劳动的水平。因此，教师应充分重视数学建模，鼓励学生自主体验来自真实生活的问题解决，开展具有创造性的脑力劳动和体力劳动，从而发展劳动能力，同时感悟数学价值。

例如，《解三角形》一课，设计课外活动任务：实地测量教学楼高度。首先，准备测距仪、经纬仪、三角板、量角器、卷尺等工具，让学生熟悉它们的使用方法，并进行简单测量实践。其次，让学生3—5人为一组，进行学校尖顶教学楼高度测量的方案设计、实地测量、数据处理、报告撰写。

整个活动中，学生置身现实情境，以劳动者的身份自主构造数学模型，然后根据实际情况，将模型合理化，最终利用正弦定理等解决测量问题，并将方案一般化如下：

如图3，设楼高为DC′，测量仪高h。在△ABD中，由正弦定理知DB=lsin βsin（α-β）。在Rt△BCD中，由正弦定理知DC=DBsin α=lsin αsin βsin（α-β）。所以，DC′=DC+h=lsin αsin βsin（α-β）+h。

从熟悉测量工具开始，到亲历测量过程，再到创新优化，学生在合作劳动中体会了学以致用的“乐”，克服了纸上得来的“浅”。数学终究不是“讲”出来的，而是“做”出来的。在这个过程中，脑力劳动与体力劳动相辅相成，学生在学科背景下体验劳动创造。

参考文献：

[1] 顾明远.高度重视学校劳动教育的育人功能和组织[N].中国教育报，20190504.

[2] 曹彬.高中数学课堂中劳动教育的渗透[J].教学与管理，2020（1）.

[3] 檀传宝.劳动教育的概念理解——如何认识劳动教育概念的基本内涵与基本特征[J].中国教育学刊，2019（2）.

[4] 任子朝，赵轩.创设真实情境突出学科特点落实“五育”要求——数学高考加强体美劳考查[J].数学通报，2019（7）.教材教法