一类新特征函数的应用
赵 亮,韩朝阳
(哈尔滨理工大学 理学院,哈尔滨 150080)
0 引 言

1 基本概念
在本文中,以X表示Banach空间,S(X),S(X*)分别表示X及其对偶空间X*的单位球面。
对于∀x∈X,取定一个fx∈S(X*)满足fx(x)=‖x‖,这样便得到一个X到S(X*)映射
x→fx
并约定对∀a>0,fax=fx。
考虑文[5]P.21的(1):对于z1,z2∈S(X),λ>0有
fz1+λz2(z2)≥‖z1+λz2‖-‖z1‖≥λfz1(z2)
(1)
文[6]后来证明了式(1)对于一切z1,z2∈X和实数λ均成立。
在文[6]中定义了[0,+∞)上的关于t的实函数fx+ty(x),fx+ty(y)。并且证明了fx+ty(y)单调递增,fx+ty(x)单调递减。

定义1[4]函数
被称为是Banach空间X的广义凸性模。
定义2[7]函数
x,y∈S(X)},α∈(0,1)
被称为是Banach空间的广义光滑模。
定义3设M={(x,y)∈S(X)×S(X),∃fx∈S(X*),fx(x)=‖x‖,fx(y)=0}。

这里的α便是广义凸性模,广义光滑模中的α。





当g′(s)存在时

文[8]的结果表明
因而g′(t)=N±(x+ty,y)=fx+ty(y),

证闭。
2 主要内容
在给出了一些说明与基本定义之后,下面便是对广义凸性模,广义光滑模与特征函数关系的探讨,于是我们可以得出下面的定理与推论。

其中α′=min{α,1-α}。
证明:先证明不等式的右半部分成立
δX(α)(t)=inf{1-‖αx+(1-α)y‖:x,y∈S(X),‖x-y‖≥t}=
inf{1-‖x+(1-α)(y-x)‖:x,y∈S(X),‖x-y‖≥t}=
S(X),‖x-y‖≥t}
由式(1)得

(1-α){1-fx(y):‖x-y‖≥t,x,y∈S(X)}。

由于fy∈S(X*),所以‖fy‖=1,|k1|=|fy(k1y+k2x)|≤|k1y+k2x|,∀k1,k2∈R。
即有 |k1y+k2x|≥|k1|,∀k1,k2∈R。
(ⅰ)若‖y+4tx‖≥2,则
(ⅱ)若‖y+4tx‖<2,‖y+4tx‖-1<2t,则
(ⅲ)若‖y+4tx‖<2,‖y+4tx‖-1>2t,则

综上可得

(1-α)[1-sup{fx(y):‖x-y‖≥t,x,y∈S(X)]≤
(1-α)[1-sup{fy+4tx(y):(y,x)∈M}]=cα(4t)

下面证明不等式的左半部分成立。

x,y∈S(X),‖x-y‖=t}=
S(X),‖x-y‖=t}≥
S(X),‖x-y‖=t}]
由式(1)有
‖x-y‖=t}]=
注意此时





则有


x,y∈S(X),‖x-y‖=t}≥
S(X),‖x-y‖=t}]
由本文中的式(1)有
此时







则

由此我们可以得出这样的一个推论:
推论1X一致凸当且仅当

其中α′=min{1-α,α},0≤t≤α′。
证明:
(1-α):x,y∈S(X)}≥
(1-α):(x,y)∈M}≥


(由于fx(y)=0,由fx+sy(y)的单调递增可知fx+sy(y)≥0)
下面不等式的左半部分成立

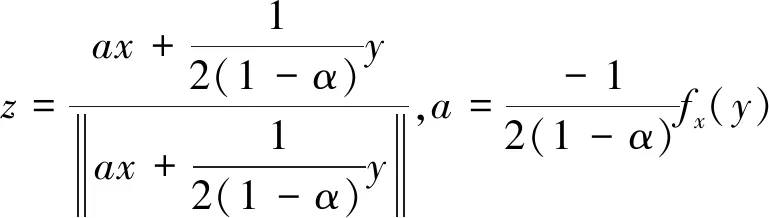
则fx(z)=0,从而(x,z)∈M。


即
所以


(x,z)∈M。
而
又
所以
综上定理2得证,于是我们可以得出下面的一个推论。
推论2X是一致光滑的充分必要条件为

