可信测度空间下的似乘算子模糊概率积分研究
赵 辉,姜欣格,单云霄
(哈尔滨理工大学 理学院,哈尔滨 150080)
0 引 言
1974年,日本学者Sugeno首先提出了模糊测度与积分的概念。模糊测度作为一个全新的理论得到了快速的发展。模糊积分作为由传统积分演化而来的一种积分,具有两种形式一种是具有可加性的模糊积分;另一种是不具有可加性的模糊积分,后者是现在研究的主要内容。
1984年王震源[1]定义了集函数的“自连续”与“零可加”。2002年HABIL E等[2]研究了经典概率论在模糊概率论中是否具有有效性的问题,由此提出了模糊概率的概念,并将一般变量演变为模糊随机变量,在模糊概率条件下证明了中心极限定理。2003年[3]EN-LIN LÜ等利用区间概率对模糊事件的随机变量进行了研究,最终得到了模糊概率定理,与此同时还对其数学期望和方差的相关内容进行了研究。2005年MESIAR R[4]首先对一般的模糊积分及性质进行了研究,又对正则模糊积分进行了研究,最后将模糊测度与积分进行了总结。2006年成和平[5]对模糊值函数的Sugeno积分进行了研究,得到了当函数a.e.相等时,两个函数积分极限相等;函数积分、极限均相等时,两个函数积分极限相等。
2010年曹兴阳[6]先从经典测度的角度研究了随机变量的收敛性,又运用概率论语言对概率进行了研究,并对其收敛性进行分析。同年,李艳红等[7]在广义Sugeno条件下,对一种非负可积函数积分的确界形式进行研究,又得到了一些运算性质。MERIGO J M等[8]在模糊概率中加入加权平均算子来进行广泛的聚合运算。
模糊积分在模糊数学中占有重要的地位,其中非可加的模糊积分受到学者们的广泛关注[9-15],2012年Liu Y[16]等在直觉模糊值Sugeno积分的基础上研究了区间模糊值Sugeno积分。2015年HALAR等[17]对离散SUGENO积分进行分析得到了一些新的性质。SMREK P[18]在2015年对几种Sugeno积分进行了对比分析。2016年TAJNER-PAPUGA I[19]以模糊测度为背景建立积分,得到了Sugeno积分特定模糊量的均值。2017年时婧婧[20]构造了模糊贝叶斯概率评估模型,用来解决网络信息安全问题,得到了较好的效果。
本文主要通过t-模和s-模定义条件设计了一个似乘算子和似和算子,重点对似乘算子进行了研究,在可信测度空间上结合似乘算子,重新定义了广义Sugeno模糊概率积分,根据演化的Sugeno模糊概率积分定义获得了此积分的一般性质及弱绝对连续性,并给出了可测函数a.e.相等时,测度是零可加的等一些定理的证明。
1 预备知识
定义1设X为非空集合,由X的一些子集构成的σ-代数即为F,集函数μ:F→[0,∞]是F上的模糊测度,若满足:
1)μ(∅)=0;
2)A∈F,B∈F,A⊂B⟹μ(A)≤μ(B);
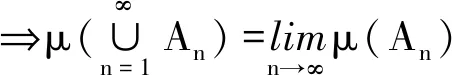
且∃n0使

当μ满足1),2),3),μ称为下半连续模糊测度;当μ满足1),2),4),μ称为上半连续模糊测度。
若μ是可测空间(X,F)上的模糊测度,则(X,F,μ)称为模糊测度空间。

1)μ(∅)=0,μ(X)=1;
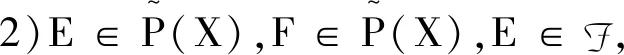

定理1概率空间为(X,A,P),概率测度P:A→[0,1]满足以下条件:
1)P(X)=1;
2)∀i≠j,Ai∩Aj=∅,
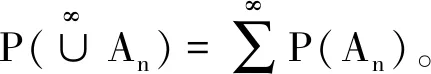
如果{An}满足A1⊆A2⊆…⊆An⊆…,则称{An}为单调增序列,记为“An”;
如果{An}满足A1⊆A2⊆…⊆An⊆…,则称{An}为单调减序列,记为“An”。
定义3设f是模糊测度空间(X,F,μ)→[0,∞]的可测函数,记
Nα(f)={x|f(x)>α} (α∈[0,∞))
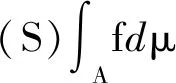
定义4映射Τ:[0,1]×[0,1]→[0,1],若∀a,b,c,d∈[0,1]满足:
1)交换律:Τ(a,b)=Τ(b,a);
2)结合律:Τ(Τ(a,b),c)=Τ(a,Τ(b,c));
3)单调性:
a≤c,b≤d⟹Τ(a,b)≤Τ(c,d);
4)边界条件:Τ(1,a)=a
则称Τ为[0,1]上的t-模算子。
2 主要结果
定义4设映射T:[0,1]×[0,1]→[0,1],∀a,b∈(0,1],构造似乘算子:

1)交换律:T(a,b)=T(b,a);
2)单调性:若a≤c,b≤d,则
T(a,b)≤T(c,d);
3)结合律:
T(T(a,b),c)=T(a,T(b,c));
4)边界条件:T(1,a)=a。
证明:
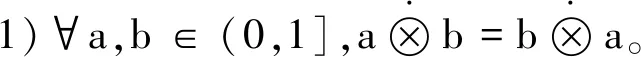
2)∀a,b,c,d∈(0,1],a≤c,b≤d⟹ab≤cd,a+b≤c+d则
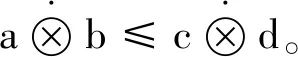
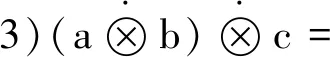

定义5设映射⊥:[0,1]×[0,1]→[0,1],∀a,b∈[0,1],构造似和算子:

1)交换律:⊥(a,b)=⊥(b,a);
2)单调性:若a≤c,b≤d,则
⊥(a,b)≤⊥(c,d);
3)结合律:
⊥(⊥(a,b),c)=⊥(a,⊥(b,c));
4)边界条件:⊥(a,0)=a。
证明:
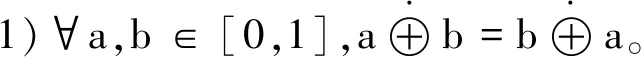
2)∀a,b,c,d∈[0,1],a≤c,b≤d⟹ab≤cd,a+b≤c+d则
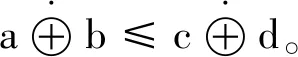

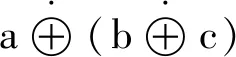

下面给出一种特殊的模糊测度——可信测度:
定义6设μ:F→[0,1]称为(X,F)上的一个可信测度,F表示一个σ-代数。当且仅当:
1)∅处为零:当∅∈F时,μ(∅)=0;
2)μ(X)=1;
3)单调非减性:∀A,B∈F,A⊂B⟹μ(A)≤μ(B);
4)可信性:若μ为(X,F)上的集函数,μ′为(X,F′)上的集函数,F⊂F′且∀A∈F,则有μ(A)=μ′(A);

则称为可信测度,可信测度是概率测度的一种特殊形式,(X,F,μ)称为可信测度空间。当且仅当∀A,B∈F,μ(B)=0且A∩B=∅,取Bn=B(n=1,2,…),有limμ(Bn)=μ(B)=0称可信测度μ是零可加的,即μ(A∪B)=limμ(A∪Bn)=μ(A)。
定理4设μ是F上的可信测度,μ′是F′上的可信测度,A,Ac∈F,μ(A)+μ(Ac)=1,则μ满足下连续性。
证明:由题意可知,对∀{An}⊂F,F⊂F′,A1⊂A2⊂…⊂An⊂…, 有
A1c⊃A2c⊃…⊃Anc⊃…,且
故有
因此μ是下连续的。
下面对可信测度空间下的广义Sugeno模糊概率积分进行研究:

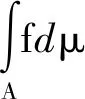
Nα(f)={x|f(x)≥α,x∈X}(α∈[0,1])
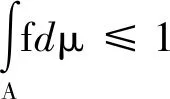
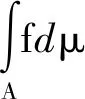
1)若f1≤f2,则
2)对∀c∈[0,1],
3)若A⊃B,则
证明:1)因为f1≤f2,根据定理2和定义7可知,有

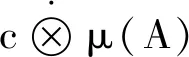
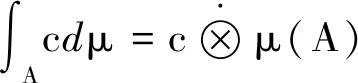
3)因为A⊃B,∀α∈[0,1],(A∩Nα(f))⊃(B∩Nα(f))
又因为μ具有单调性,所以
μ(A∩Nα(f))≥μ(B∩Nα(f))故
4)A∈F,f1,f2为可测函数,
5)A∈F,f1,f2为可测函数,
综上所述,结论成立。
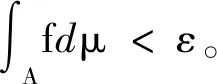
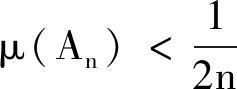
但由定义2.2知
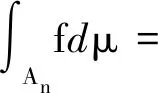
μ(An)
因此

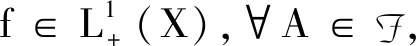
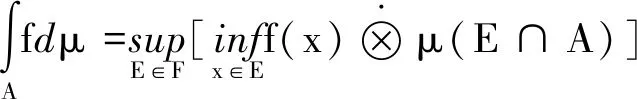
证明:∀α∈[0,1],x∈Nα(f),f(x)≥α左右同取下确界:
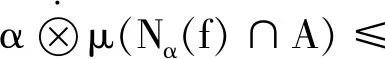
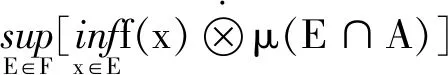
式子左右同取上确界,且式子右边与α无关,∀α∈[0,1],从而
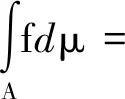

又有∀E∈F,对式子两端同时取下确界:
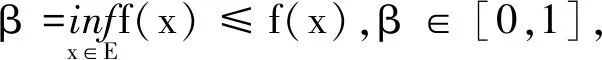
再对式子左右同取上确界,等式右边与E无关,所以
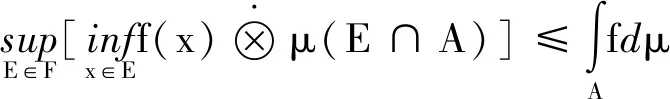
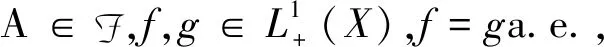
证明:
充分性:因为f=g,a.e.,设B={x∈X;f(x)≠g(x)},则μ(B)=0,∀α∈[0,1],x0∈Nα(f),即f(x0)≥α。
当f(x0)=g(x0)时,x0∈Nα(g);
当f(x0)≠g(x0)时,x0∈B,因此Nα(f)⊂Nα(g)∪B。
因为μ具有单调性和零可加性,则有
μ(Nα(f))≤μ(Nα(g)∪B)=μ(Nα(g))
则
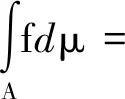


必要性(反证法):若μ不具有零可加性,则有∀A∈F,B∈F,μ(B)=0,但μ(A∪B)≠μ(A)⟺μ(A∪B)>μ(A)。
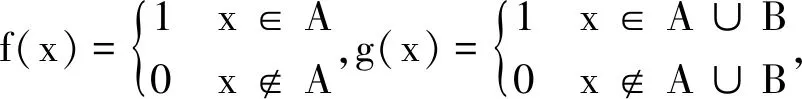
{x∈X;f(x)≠g(x)}=
(A-A∪B)∪(A∪B-A)=
(A∩(Ac∩Bc))∪((A∩Ac)(B∩Ac))=
B∩Ac⊂B
因此
0≤μ({x∈X;f(x)≠g(x)})≤μ(B)=0⟹f=g有
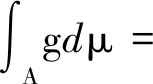
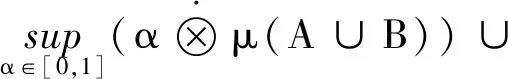
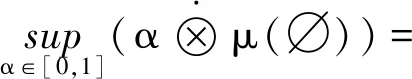

μ(A∪B)
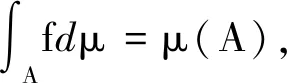
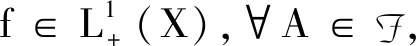
证明:设
B={x∈A;f(x)≠0}={x∈A;f(x)>0},C={x∈A;f(x)≠0},
则A=B∪C,A∩B=∅,μ(B)=0,∀α∈(0,1],有
0≤μ(Nα(f)∩B)≤μ(B)=0,
Nα(f)∩C={x∈A;α≤0}=∅
因此
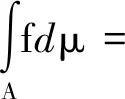
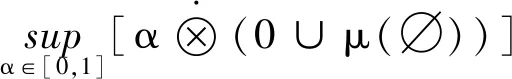
=0
综上所述,结论成立。
3 结 论
本文构造了一个模糊似乘算子和似和算子,证明该算子满足t-模和s-模条件,又建立了一个新的测度空间—可信测度,主要研究了在可信测度空间下将模糊似乘算子与Sugeno模糊概率积分相结合得到的新积分形式并证明相关的定理和性质均成立。对于模糊似和算子的部分将在后续研究中作为重点内容进行深入研究。

