基于优化列文伯格-马夸尔特法的SLAM图优化

戴天虹，李志成

(东北林业大学 机电工程学院，哈尔滨 150036)

0 引 言

自身定位和地图构建是研究移动机器人领域的一项基本任务。随着移动机器人关键技术的发展，移动机器人的自主导航成为该领域的研究热点之一。移动机器人在未知的环境中根据传感器获取的数据并同时估计自身的位姿和周围的环境地图，这个问题被称之为即时定位与地图创建[1-2](Simultaneous Localization and Mapping SLAM)。移动机器人的即时定位与地图创建是以可移动的机器人为主体，搭载特定的传感器，在无先验信息的环境下，从一个未知位置开始运动，在运动过程中根据传感器信息估计自身位置，并同时建立周围环境模型的关键技术。早期的SLAM技术中一般采用激光测距仪[3-4]作为传感器，利用基于滤波的方法优化数据集。近年来，由于计算机视觉的不断发展，搭载视觉传感器的SLAM已经成为主流，主要有单目相机[5-6],双目相机[7],多目相机[8]和RGB-D传感器[9]等。随着图优化理论的应用，非线性优化的方法逐渐代替基于滤波优化数据集的方法受到了研究者的广泛关注。相对于传统SLAM技术中Smith R等人提出的基于扩展卡尔曼滤波方法(extended Kalman filter EKF)[10],图优化技术在G2O(general graph optimization)[11]、Ceres[12]等框架下的实现既提高了移动机器人获取相对位姿的准确性，又能有效提高计算效率，但仍然存在特征点的检测和匹配精度低、优化速度慢、算法复杂、建图效果不显著等诸多有待解决的问题。

针对视觉SLAM后端处理中，优化过程冗杂、优化速度慢、优化精度较低等缺点，本文首先介绍了视觉SLAM系统和SLAM系统下的状态描述；其次，阐述传统的非线性优化方法和经过优化后的非线性优化方法理论，并通过仿真实验进行对比说明。最后，通过完成对原始的三维点云地图的优化实验对比分析，并进行相应的说明。

1 视觉SLAM系统

经过长达十多年的发展，视觉SLAM的基本框架已经日渐成熟。视觉SLAM主体框架由传感器部分、视觉里程计(visual odometry)、后端优化(optimization)、回环检测(loop closing)和建图(mapping)5个部分组成。

传感器部分在视觉SLAM中主要负责RGB图像和Depth图像的获取，并且进行一定的预处理操作。SLAM前端主要任务是根据移动机器人在场景中不断变化的位置时视觉传感器的输出结果，通过特征匹配和特征检测，估算相邻图像间的旋转矩阵和平移向量[13]，并且可以通过视觉传感器输入的视频流[14]，获得不断更新的局部地图。SLAM后端是指SLAM技术中的后端优化，这一部分是为了处理SLAM中的噪声问题而设置的。现实环境中，视觉传感器获取的数据信息带有大量的噪声，即便是精度再高的传感器也无法避免这项缺陷。后端优化是依据视觉里程计测量的不同时刻下机器人位姿信息，通过滤波、非线性优化算法等方法对它们进行优化的过程，是获取全局地图的必要条件之一。回环检测[15]是利用图像信息丰富的优势，通过两帧图像间的相似性对比，判断移动机器人是否到达过之前已经到达过的位置。回环检测的设置，是为了解决机器人在移动的过程中位姿估计随时间漂移的问题。SLAM中引入回环检测，即引入时间间隔更久远的约束，并将此约束传递给后端进行优化，从而得到全局一致性的位姿估计，保证了在长时间的运动过程中所估计出的机器人运动轨迹和地图的正确性[16]。建图是构建地图的过程，大体可分为构建拓扑地图和构建度量地图。

1.1 基于图优化的视觉SLAM系统

目前SLAM中的主流优化方法是基于图优化技术建立位姿图，即对环境中特征点的观测通过边缘化的方法转换为机器人不同时刻位姿间的约束，通过对机器人的位姿及环境中的特征点位置序列进行估计来简化优化。其中，位姿图中的节点对应于每个时刻机器人的姿势和当下时刻观测到环境中的特征点，位姿图中的边对应于节点之间的空间约束。通过不断调整位姿图中节点的位置，使其符合边的空间约束，进而得到机器人的运动轨迹与所观测到的环境地图。基于图优化的视觉SLAM系统，如图1所示。

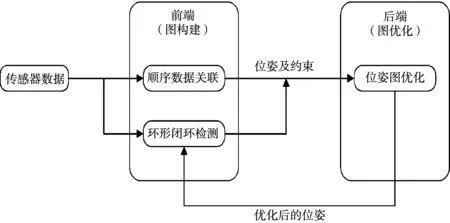
图1 基于图优化的视觉SLAM系统Fig.1 Visual SLAM system based on graph optimization

BA(bundle adjustment)[17],又名光速平差法，是指能够从视觉重建模型之中提取出相应的相机内、外参数以及最优的三维模型的一种方法。BA优化作为图优化框架下的视觉SLAM算法中的核心算法，具有将位姿与路标同时调整的优化能力。早期的BA算法理论，在测量学中有广泛的工程应用，很少用于视觉图像方面。随着计算机视觉技术的发展，研究者们才将BA算法逐渐引至视觉图像研究领域，才使其在视觉图像方面的应用以及理论的创新逐渐称为研究热门。直到近十年，由于BA的稀疏特性，该方法才被广泛应用于SLAM问题研究中，并在实时的场景中得到很好的应用。BA在SLAM技术中的应用，主要体现在SLAM后端的优化过程中。BA 算法在以图优化为主体框架的视觉SLAM中，可以将一个复杂的最小二乘问题转变成由节点和边构成的问题，能够直观的描述相机运动行为。这种方法，将SLAM中复杂的非线性最小二乘问题通过图论的方式直观表述，易于后期研究和优化，同时体现了图优化的核心思想。

1.2 SLAM状态描述

SLAM技术中采用不同的传感器，会有不同的参数化形式。如果要保持其通用性，可以取成通用的抽象形式，即用运动方程和观测方程来描述，

k=1,…,N;j=1,…,M

其中：x是位姿点描述；xk是在k时刻的位姿；uk是运动传感器的读数；wk为噪声；当视觉机器人在xk位置上看到某个路标yj，产生一个观测数据zk,j，vk是这次观测里的噪声。运动方程描述了状态xk-1如何变到xk，而观察方程式描述的是从xk是怎么得到观察数据yj的。

运动方程和观测方程都容易受到噪声的影响，通常把位姿x与路标y看成符合概率分布的随机变量，假设状态量和噪声项服从高斯分布。通过计算对变量最优值的估计(即均值)以及度量均值的不确定性(即协方差)，来估计状态量的高斯分布。

在运动方程和观测方程中，通常假设两个噪声项wk和vk分别满足N(0,Rk)、N(0,Qk,j)的零均值高斯分布。

2 优化L-M下降策略

2.1 传统的L-M下降策略

因为噪声的存在，SLAM中运动和观测方程的状态计算值和系统估计的轨迹存在一定的误差，通过优化方法对状态计算值进行微调，使这项误差下降到一个极小值，这个过程是一个典型非线性优化的过程。因此，引入最小二乘的问题，如式(1)：

(1)

其中f是任意非线性函数。此公式能计算出系统的极值点，并通过直接比较可获得理想值。

高斯牛顿法(G-S)[18]是最基本的非线性最小二乘方法，是将目标函数f(x)在x附近进行一阶泰勒展开，如式(2)：

f(x+Δx)≈f(x)+J(x)Δx

(2)

其中，J(x)是f(x)关于x的导数。欲使‖f(x)+Δx‖2达到最小值，目标是寻找最合适的Δx，

将目标函数Δx*求导并令其导数等于零，得到线性方程：

J(x)TJ(x)Δx=-J(x)Tf(x)

为方便记忆，将左边的系数定义为H，右边的定义为g，记为式(3)：

HΔx=g

(3)

列文伯格-马夸尔特法(L-M)[19]是基于G-S法基础上的一种改进方法，其核心思想是在每一个最优优化算法里，需要通过迭代来获得目标函数的极小值，且在每次迭代中的目标函数的值都是下降的，即给Δx添加了一个信赖区域。在L-M优化中，需要将带有不等式约束的优化问题变成一个无约束的优化问题，转化中需要引进拉格朗日算子λ，

其中，D是信赖区域。计算增量的线性方程类似于高斯牛顿法中的处理方法，

(H+λDTD)Δx=g

简化形式，

(H+λI)Δx=g

其中D=I。

L-M法中，信赖区间的范围是根据近似模型和实际函数之间的差异确定的，可以通过式(4)判断近似的效果好坏。

(4)

若ρ值太小，说明实际减小值远小于近似减小值；若ρ值太大则意味着实际下降值超出预计。ρ值接近于1时，是近似最好的效果。

虽然L-M法在G-S法的基础上进行了一定改进，但仍存在不足。当参数λ比较小时，I的影响力远远小于H占据的地位，导致二次近似模拟在该范围内更适合，这时候更接近于G-S法; 当λ比较大时，I的影响力远远大于H占据的地位，导致二次近似模拟在该范围内不理想。

2.2 优化的L-M下降策略

本文就传统的L-M法中对于拉格朗日算子λ的取值没有限制，会出现过大或者过小取值的情况，因而造成增量Δx的不稳定、不精确的情况，设计一种改进的L-M法下降策略以解决λ取值问题。

在迭代的过程中，把增量限定于一个圆球中，该圆球的半径为μ，增量只有在圆球内才被认为是有效的。这种设计直接把x约束到一个圆球中，信赖区域用D表示，并将D取成非负数对角阵，使约束范围在该梯度方向上稍大一些。本文改进的---法下降策略方法：

1)给定系统的初始值x0以及初始优化信赖区域半径μ；

2)求解第k次迭代下方程的解并事先确定ρ值，

3)通过拟定一个阈值和扩大倍数，检测泰勒近似效果是否足够好，

4)当ρ大于等于事先选定的某个阈值并且当下算法收敛，则可认为该近似是可行的，迭代结束；否则，令xk+1=xk+Δx重复上述步骤。

优化后的L-M下降策略框架中，近似范围扩大的倍数和阈值是可自定义的，可使用经验值代替。通过一个拟定的阈值和扩大倍数检测泰勒近似是否足够好，若不够满意则通过将信赖区域进行简单的放大或者缩小，进而继续寻找信赖区域内的最优下降策略。这种基于L-M法的优化下降策略能提高优化系统的效率和系统的鲁棒性，具有良好的工程实践应用性。

2.3 优化的L-M法仿真实验

本实验基于观测数据，将通过G2O 进行曲线拟合，拟合曲线为，

其中，a、b、c为曲线的参数，w为高斯噪声。假设N个关于x、y的观察数据点，通过求解最小二乘问题来估计曲线参数，

在相同的实验环境下，通过G2O库优化分别采用传统的L-M下降策略和优化的L-M下降策略进行仿真实验，得到的结果如图2和图3所示。

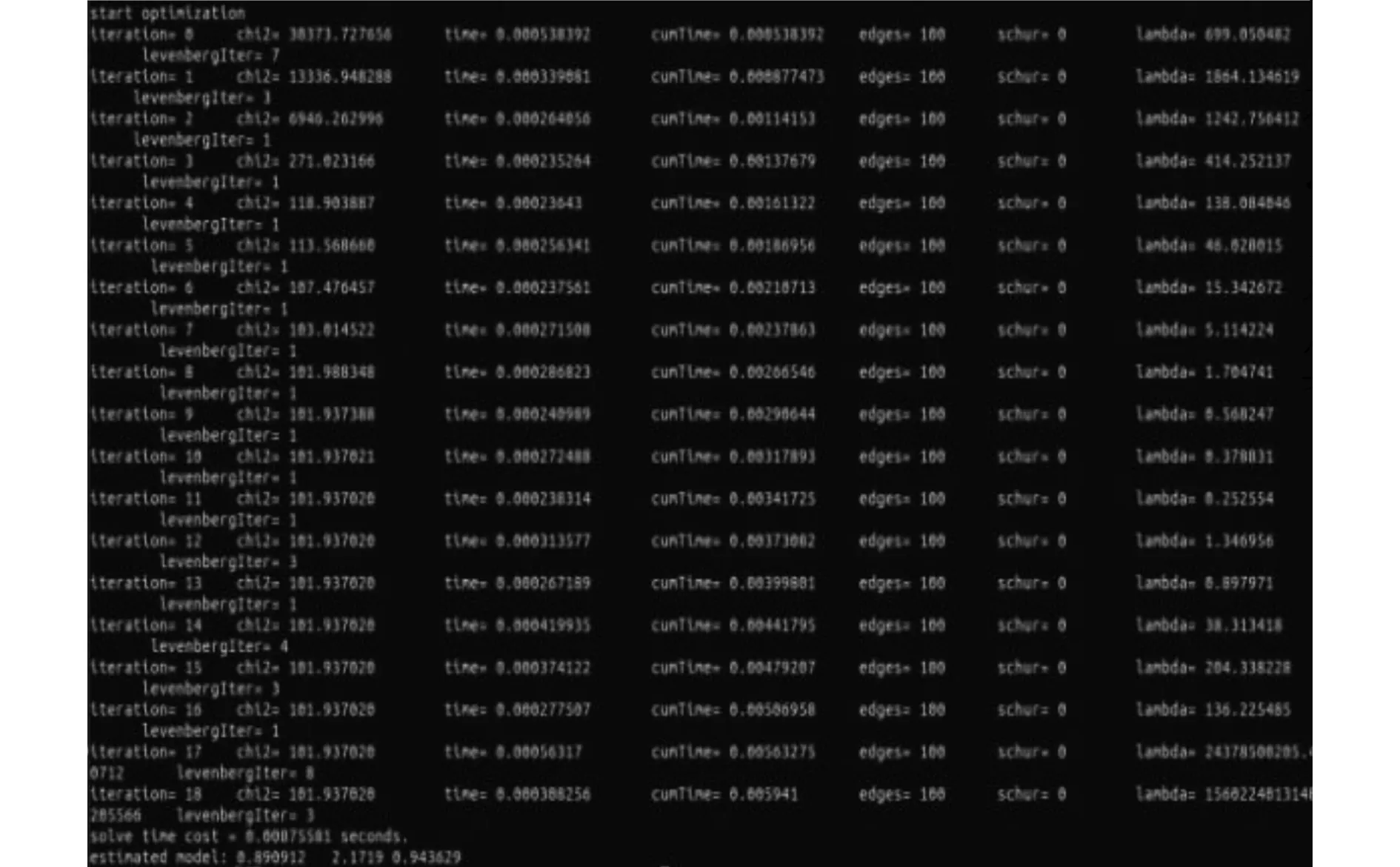
图2 传统的L-M下降策略拟合Fig.2 Traditional L-M descending strategy fitting

图3 改进的L-M下降策略拟合Fig.3 Improved L-M descending strategy fitting

通过上述仿真实验，对实验结果进行总结，如表1所示。

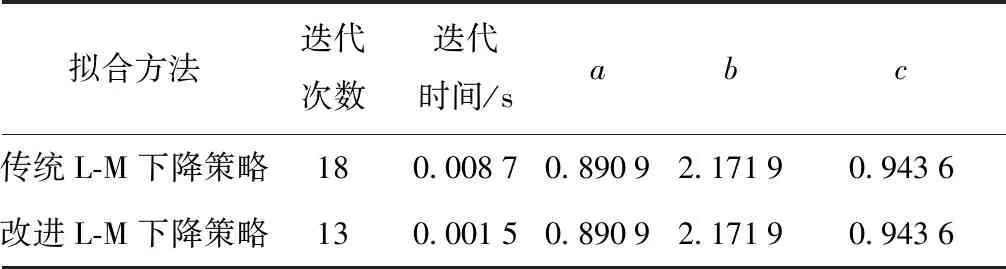
表1 曲线拟合Tab.1 Curve fitting

在同等实验环境的梯度下降策略中，相比于传统的L-M法下降策略，改进后的L-M法下降策略所需迭代次数更少，迭代时间更短，效率有所提高。

3 三维点云的BA优化仿真实验

本文采用的开发环境是Linux系统，开发平台是Ubuntu 16.04。Ubuntu 16.04为以Linux系统为基础开发的图形界面的操作系统。计算机具体参数为：华硕笔记本，型号：A55V，CPU：Intel酷睿i53210M，CPU主频：2.5GHz，内存容量：4GB。

G2O(general graphic optimization)是一个用C++开发的用于求解非线性最小二乘问题的开源库[20]。它提供了大量的顶点和边的类型，是一个基于图优化的库。在工程实践中，G2O可以求解很多将优化表达成图的问题，对于相机位姿估计问题十分方便。

本文采用来自于华盛顿大学 GRAIL 实验室发布于 GitHub网站上的公开数据集作为三维点云实验原始数据，从“Community Photo Collections”项目中可获取该数据集。基于BA中的稀疏特性，选用稀疏求解器作为G2O中使用的线性求解器。定义传统的L-M方法和基于L-M法的优化下降策略通过相同实验环境的对比，观察和分析三维点云的重建效果。

如图4所示，是一张未优化的三维点云地图。地图中，像素点散乱，不具有可观性。

在G2O优化框架下，下降策略选用传统的L-M方法，

如图5和图6所示，在G2O框架下，传统的L-M法下降策略经过 19 次迭代，每次迭代的时间大约为 2 s。优化后的三维点云地图结构虽然比较清晰，但依旧存在很多点云模糊的情况。

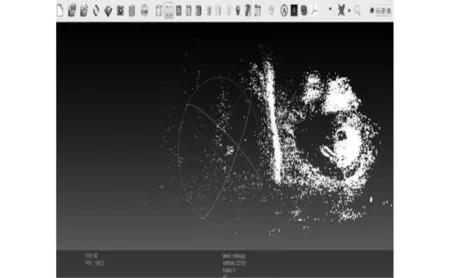
图4 未优化的三维点云地图Fig.4 Unoptimized 3d point cloud map

图5 传统的L-M法下降策略实验数据Fig.5 Experimental data of traditional l-m descending strategy

图6 传统的L-M法下降策略优化后的三维点云图Fig.6 3D point cloud map optimized by the traditional l-m descending strategy

在G2O优化框架下，下降策略选用优化的列文伯格-马夸尔特方法。

如图7和图8所示，在G2O框架下，改进的L-M下降策略经过 16 次迭代，每次迭代的时间大约为 0.17 s。相比传统的L-M下降策略，优化后的三维点云地图结构更加清晰明了，混乱的点云扎堆的情况减少了很多，达到了优化改进的效果。将使用传统的L-M法和优化后的L-M法的处理结果汇总于表2。

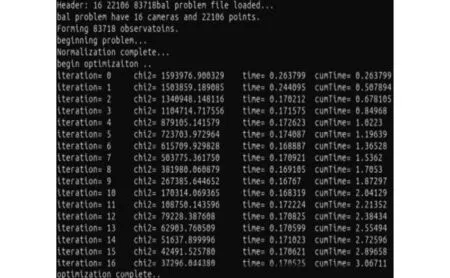
图7 改进的L-M下降策略实验数据Fig.7 Experimental data of improved l-m descending strategy

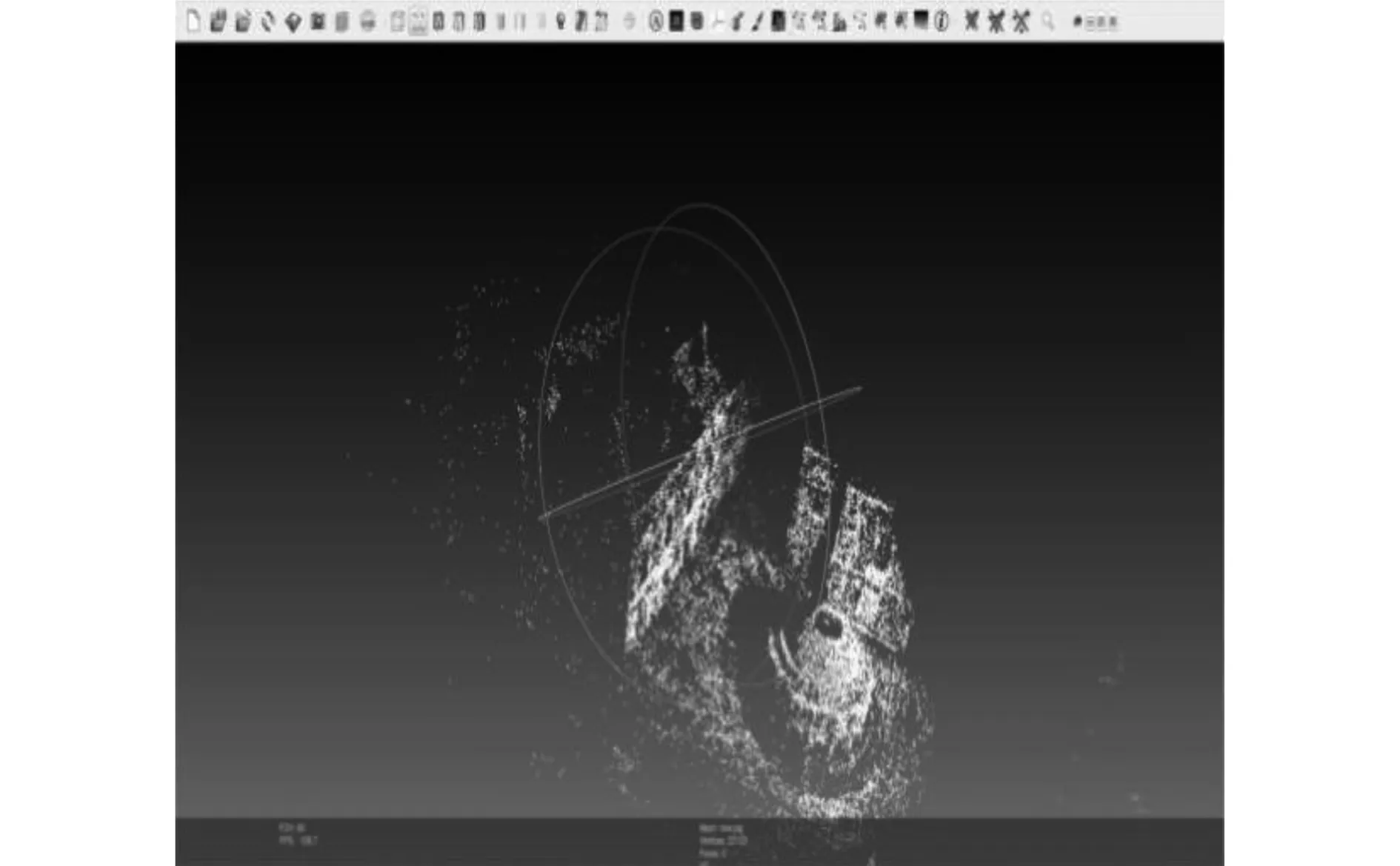
图8 改进的L-M下降策略优化后的三维点云图Fig.8 3D point cloud map optimized by improved l-m descending strategy

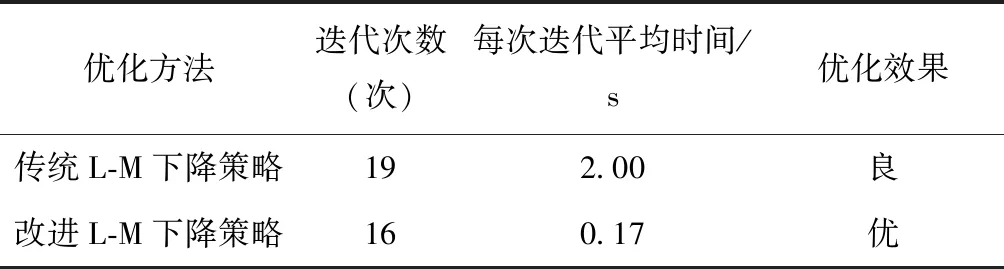
表2 实验参数对比Tab.2 Comparison of experimental parameters

由表2可知，经过优化后的L-M下降策略，在迭代次数由原来的 19 次缩减到现在的 16 次，每次迭代平均时间明显优于传统的L-M法下降策略，总体优化效果有显著提高。

4 总 结

针对SLAM的优化问题，在已有的BA非线性优化方法的基础上，采用一种基于改进的L-M下降策略，优化后的下降策略核心在于事先确定一个阈值并且可以在拟定参数的扩大倍数范围内，限定每次迭代的信赖区域达到优化的效果。通过对GRAIL实验室在GitHub网站上的公开数据集中原始三维点云地图的优化实验，使用G2O完成对BA优化方法的研究，分析其仿真结果得出经过优化后的L-M法下降策略能够提高优化速度，可以显著提升建图效果，并能应用于三维重建和视觉SLAM图优化技术中的结论。但SLAM技术中仍有诸多环节存在精度不高，优化效果不明显等有待解决的问题。因此，需要进一步的优化算法，以达到更好的实时性。