电容层析成像系统传感器场域剖分及参数优化
张晋荣,王莉莉,杨博韬,刘 笑
(哈尔滨理工大学 计算机科学与技术学院,哈尔滨 150080)
0 引 言
电容层析成像(electrical capacitance tomography,ECT)技术是自20世纪80年代借鉴医学CT技术发展起来的一种成本低廉且安全性能高的新型流动层析成像技术[1],因其具有结构简单、响应速度快等诸多优点,被广泛应用于工业管道中两相流或多相流的测量过程中。它可以在不破坏封闭管道内多相流混合体结构的前提下,采用均匀安装在管道周围的阵列式电容传感器来获得被测区域在不同角度或方向上的多个电容测量值,并将这些电容测量值作为投影数据由计算机采用某种图像重建算法[2],计算出各分相介质的浓度大小、分布状况等相关过程参数。
1 电容层析成像系统的组成结构
一个典型的12电极ECT系统一般由传感器系统,电容数据采集及信号处理系统和图像重建系统三部分组成(如图1所示)[3]。电容传感器是ECT系统的重要组成部分,其结构如图2所示,主要由绝缘管道、测量电极以及接地屏蔽罩3部分构成。传感器性能的好坏将直接影响电容值的测量精度以及电极间敏感场分布的均匀性,进而影响着数据采集系统的可靠性和图像重建的质量,因此合理选择传感器结构参数的工艺材料及物理尺寸,从而获得灵敏度高且可靠性强的电容传感器,对提高ECT系统的整体性能有着深刻的意义。

图1 12电极ECT系统结构图Fig.1 Structure of 12-sensor ECT system
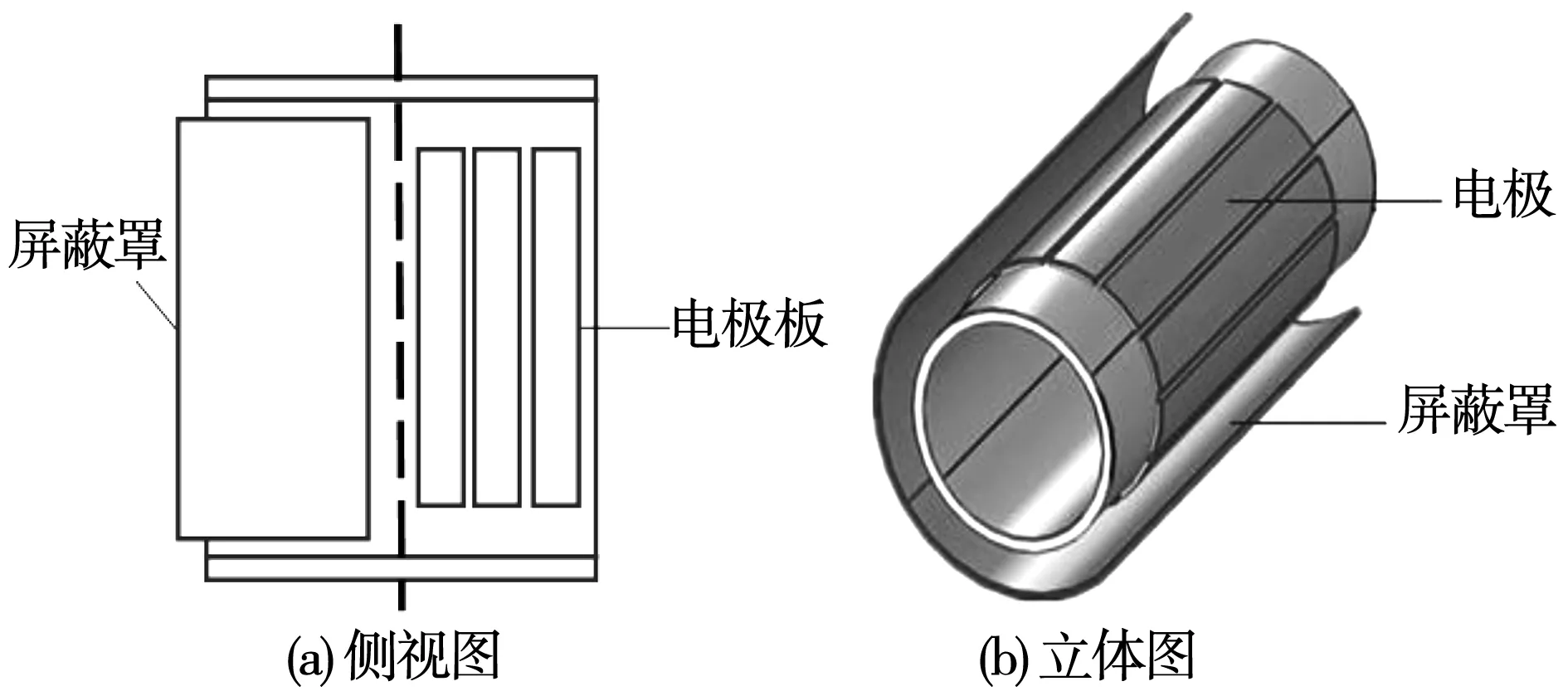
图2 传感器结构图Fig.2 Structure of sensor
2 电容传感器的数学模型
由电磁场理论可知,电容传感器内的电磁场可被认为是稳定的静电场,即场内无自由电荷[5]。因此,传感器内的电位分布满足静电场的拉普拉斯方程,见式(1)。
▽·[ε0ε(x,y)▽φ(x,y)]=0
(1)
式中:ε(x,y)和φ(x,y)分别为介电常数分布函数和电势分布函数,▽·和▽分别为散度算子和梯度算子。当电极i为源电极(激励电极)时,其相应的边界条件可表述为:
(2)
式中:Γi、Γs、Γg分别为电极i(i=1,2,3,…,12)所在位置、屏蔽层位置和径向电极所在位置。电场强度E(x,y)可表述为:
E(x,y)=-▽φ(x,y)
(3)
当电极i为激励电极且电极j为检测电极时,由高斯定理可得电极j上的感应电荷Qi,j为:

(4)

当Qi,j确定后,电极i和电极j之间的电容Ci,j为
(5)
式中Ui,j为电极i和电极j之间的电压。
ECT系统中的研究问题主要分为正问题求解和反问题求解这两类研究问题。对正问题的研究通常包括两部分:一是已知被测区域的介电常数分布ε(x,y)以及相应的边界条件,通过计算得到该介电常数分布下各电极间的电容值;二是仿真计算电极间相应的敏感场分布,为图像重建提供先验数据。而反问题求解过程则是将电容测量值作为投影数据,结合在正问题研究过程中获得的敏感场分布,进行图像重建。电容层析成像系统中正问题的求解过程通常采用有限元仿真来实现。
3 电容传感器的有限元模型及敏感场计算
3.1 传感器的有限元模型
有限元法是一种被广泛应用于求解工程问题近似解的高效数值分析法。该方法将待求解区域剖分为一系列仅由节点连接的微小单元,并为每个微元进行分片插值,从而将偏微分方程求解问题离散为普通多元函数的极值问题,最后通过求解代数方程得到偏微分方程的数值解。场域的剖分问题是利用有限元法求解问题的关键,剖分结果的优劣将对ECT系统中正问题的求解结果以及重建图像的准确性产生直接的影响[6]。因此在网格剖分时应特别注意:
1)在需要详细分析的区域(场变量变化强烈的区域),其单元剖分的密度应高于其他区域。
2)要尽可能使得剖分结果的对称性与传感器的对称特性相一致,以便于完成电容敏感场的数值计算。
3)尽量使每个剖分单元各边的长度相等,一般不宜超过3∶1,避免出现尖锐的单元。
根据以上3点要求,本文将三角形剖分与四边形剖分相结合对传感器的敏感场进行剖分。剖分结果如图3所示,由于场域内不同位置的敏感强度不同,因此采用一种不均匀且不等间距的剖分方式进行剖分,离场变量变化强烈的区域越近剖分越细。并针对电极附近场变量变化强烈的区域,即需要重点研究的区域,采用三角形剖分方式,离极板较远的管道中心以及外部绝缘层等敏感度较低的区域采用四边形剖分形式。考虑传感器的对称性,整个管道截面被分为12个扇区,并在每个扇区的内部都采用相同的剖分方式。同时,在剖分时保证了每个单元各边的长度尽可能相等。最后,管内区域共有672个节点,被剖分为684个四边形单元;管壁区域共有384个节点,被剖分为576个三角形单元;外部绝缘层区域共有192个节点,被剖分为288个四边形单元,整个管道截面共有1 248个节点,1 548个单元。从图中可以看出,最小的同心圆实际上是被剖分为12个三角形单元,但这在管内所有的684个剖分单元中只是非常少的一部分,所以对管内区域的剖分结果仍旧认为是采用了四边形剖分方式。

图3 传感器场域的剖分结果Fig.3 Sensor field domain segmentation results
3.2 电容传感器的敏感场计算
采用有限元方法将管道截面剖分成N个单元(包括所有四边形单元与三角形单元),M个节点,当电极i为激励电极时,式(1)可转换为:
Kφ=T
(6)
其中:K为M×M的系数矩阵;T为M×1的列向量。由于假设场域内无自由电荷,所以T为零向量,因此只需利用有限元法求出系数矩阵K的值,便可以求得场域内各点的电势分布。
对于检测极板j上的感应电荷Qi,j,并不能由式(4)直接求得,最常用的方法是采用模拟电荷法,利用有限元分析中获得的系数矩阵K和电势分布φ由式(7)计算出Qi,j,并将结果代入式(5)中求得极板间的电容值。
Qi,j=∑(Kφ)n
(7)
式(7)中,(Kφ)n为矩阵K的第n行与场域中节点的电势φ的标量积,其物理意义表示节点n上的净电荷量。
由于对称性使得12电极ECT系统中传感器的66个相对敏感场只有6种不同的类型[7-8],即Si,j(i=1,j=2,3,4,5,6,7),其他的敏感场可通过旋转的方法得到。定义极板间的灵敏度分布Si,j(k)为:
(8)
式中:Ci,j(k)为当管内第k个单元介电常数为ε1且其余单元介电常数为ε2时的电容值;Ci,j(ε2)和Ci,j(ε1)表示管内分别充满介电常数为ε2和ε1物质时的电容值;Ak是单元k的面积。
通过有限元法求得电容值,并将其代入式(8)中计算得到传感器的6个典型敏感场分布,如图4所示。
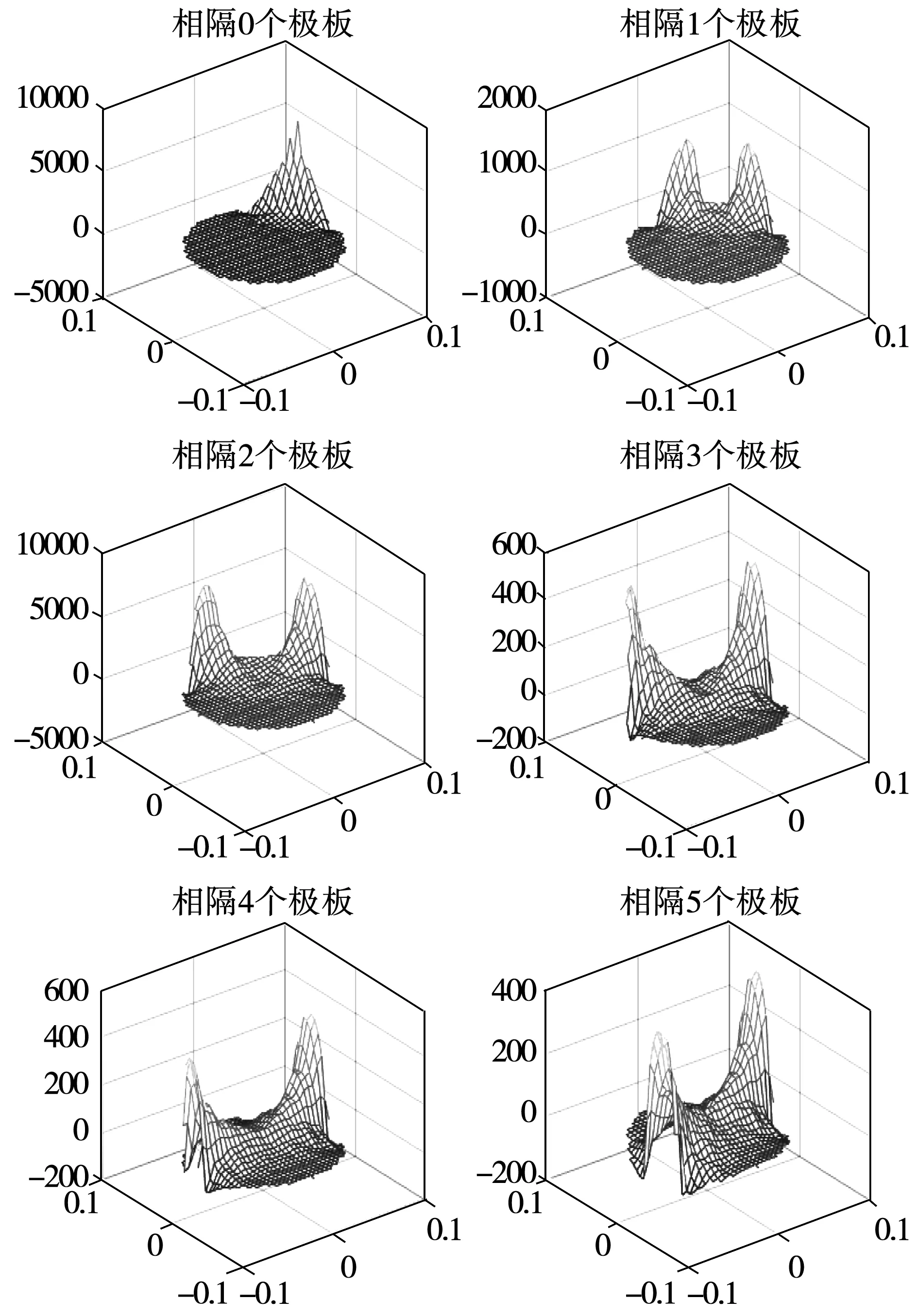
图4 传感器敏感场分布Fig.4 Sensitive field distribution of sensor
从图中可看出,相隔0个极板对(相邻极板对)间的灵敏度分布呈现单峰状,而相隔1、2、3、4、5的极板对间灵敏度分布都表现为马鞍状,这表明测量管道内的敏感场因受多相流介质分布的影响导致其分布并不均匀。在离极板较近的区域,由于场变量变化剧烈使得该区域敏感度较高,相反,对于距离极板较远的管内中心位置而言,场变量变化平缓传感器灵敏度较低,这将导致重建图像精度不高,重建效果并不理想。因此,为了提高重建图像的精度,获取均匀的灵敏度分布是非常必要的,而合理调整优化传感器的结构参数是改善敏感场的“软场特性”获得高质量重建图像的一种有效方法。
4 传感器性能优化函数的确定
由以上对敏感场特性的分析可知,使场内具有均匀相等的灵敏程度是传感器优化的主要目标。分别定义灵敏度的均值和标准差为:
(9)
(10)
其中:n为有限元剖分的测试单元数目;Si,j(k)为电极i与电极j之间第k个测试单元的灵敏度值。Savg(i,j)表示n个剖分单元的平均灵敏度,Savg(i,j)的值越大,场域的整体敏感度越高,传感器的性能就越好。Sdev(i,j)反映单个单元的灵敏度Si,j(k)相对于平均灵敏度Savg(i,j)的离散程度,Sdev(i,j)的值越小越好。
为了评估所有电极对间敏感场分布的均匀程度,定义传感器结构参数的函数P为
(11)

此外,还应考虑使最大电容Cmax和最小电容Cmin的取值都在测量电路的量程范围内。定义Kc=Cmax/Cmin,由于最大电容Cmax由相邻极板间测量流体中全管为介电常数大的相决定[10],最小电容Cmin由相对极板间介电常数小的相决定。因此,Kc越小,对电容测量电路的量程范围要求越低。
在分析了影响电容传感器性能的主要因素的基础上,定义传感器的性能优化函数如下:
G(X)=P+Kc
(13)
函数G(X)包含了影响传感器性能的两项主要指标,即传感器结构参数的函数以及最大/最小电容比值。G(X)的值越小,电容传感器的综合性能越好。
分析该优化目标函数可知,目标函数G(X)和自变量X之间并不存在明确的函数关系,因此并不能用解析法求解,通常采用正交试验法寻找最优参数。但由于正交试验中所有可能的参数组合为事先选定而非自动生成,并且试验的次数有限,因此存在一定的局限性。针对存在的问题,本文在正交试验的基础上,提出一种将RBF神经网络与改进后的基于混沌理论和模拟退火算法的粒子群优化算法相结合的方法对电容传感器的结构参数进行优化设计。
5 传感器结构参数正交试验设计
12电极ECT系统中电容传感器的截面结构如图5所示,其中θ为电极张角,R1为测量管道的内径,R2为管道中心与电极之间的长度,R3为管道中心与屏蔽罩之间的长度,h1为径向屏蔽电极的插入长度,ε3为管壁介电常数,ε4为绝缘填充材料介电常数。为了便于比较分析,在各个电极长度相等的条件下,定义基准传感器的结构参数如下:θ=22°,R1=76.8 mm,R2=86.8 mm,R3=96.8 mm,h1=0 mm,ε3=5.8,ε4=2.2。

图5 电容传感器截面图Fig.5 Sectional view of capacitive sensor
电容传感器的有关优化参数约束条件如下:
1)在本系统中,电极数N=12,电极的轴向长度l=0.1 m。对于12电极系统而言,θ必须小于30°;
2)极板半径R2>R1;
3)管道的厚度d1=R2-R1,其介电常数为ε3,采用介电常数ε3=8的陶瓷;
4)屏蔽罩与绝缘层之间的厚度d2=R3-R2,其介电常数为ε4,采用ε4=5.8的可加工玻璃;
径向屏蔽电极的插入深度h1,h1 由以上分析可知,传感器的参数优化问题是一个带有约束条件的最优化问题,优化目标函数可表示为: G(X)=f(θ,d1,R2,d2,h1) (14) 自变量X是一个包含了5项结构参数的五维向量,则最优化问题的解转换为在五维空间中寻找满足自变量取值范围且使目标函数取得最小值的点,这样的点就是最优化问题的解。 选择θ,d1,R2,d2,h1这5项结构参数作为优化试验的主要考察对象,采用5水平正交表L25(55)安排试验。表1为正交试验的具体试验方案以及试验结果。 表1 正交试验方案及结果Tab.1 Scheme and results of orthogonal experiment 试验结果的极差分析如表2所示。表2中Ki(i=1,2,3,4,5)的值分别是该列对应参数因子取5个不同水平时相应试验结果的均值。R为该列K1、K2、K3、K4、K5取值的极差,极差越大表示该因素的水平变化对G(X)的影响程度越大,即该因素对传感器的性能影响越大。 表2 试验结果的极差分析Tab.2 Range analysis of test results 由极差R的大小可知,各因素对G(X)的影响从大到小依次为电极张角θ,屏蔽罩与绝缘层之间的厚度d2,径向屏蔽电极的插入深度h1,极板半径R2,管道厚度d1。可以根据各因素所对应的5个水平的大小来确定各因素的最佳水平。由于G(X)的取值越小,传感器的性能越好,通过上述正交试验得到一组优化参数:θ=24°,d1=16 mm,R2=88 mm,d2=30 mm,h1=4.5 mm。利用有限元法进行仿真计算,得到这组参数对应的G(X)的值为4.212 68,优于已有的25次试验结果,可以把这组参数作为电容传感器优化设计的参考依据。 RBF神经网络,即径向基函数神经网络,是一种包括输入层、隐藏层和输出层的三层前向神经网络,其结构如图6所示。 图6 RBF神经网络结构Fig.6 RBF neural network structure 一般的线性回归或多项式回归方法并不能准确地反映传感器的结构参数与优化目标函数之间复杂的非线性关系,而RBF神经网络能够在一定条件下以任意精度逼近任意的非线性函数,反映系统内难以解释的规律。因此,本文采用RBF神经网络对正交设计的试验结果进行回归分析。 从表1的25组试验数据中随机选取20组作为训练样本,另外5组数据作为测试样本。设置误差参数为0.000 1,并将隐含层中神经元的最大数目设为20。在回归分析前,需要对表1中正交设计的试验数据进行归一化处理,处理方法如下: d1′=R2-R1/R1,d2′=R3-R2/R1 h1′=h1/R1 采用归一化后的试验数据作为RBF神经网络的输入,G(X)作为神经网络的输出,经过训练得到回归模型。并通过将5组测试样本的预测结果与有限元仿真获得的结果进行比较来验证该回归模型的预测能力。由表3中的实验结果可知,回归模型的预测误差处于0.69%~1.32%之间,表明具有良好的预测能力,能够很好地应用于粒子群算法中各粒子的适应度值计算中。 表3 预测值与仿真值对比表Tab.3 Comparison table between prediction values and simulated values 粒子群优化(PSO)算法是一种基于群体协作的随机搜索算法,1995年由Eberhart和Kennedy提出[12],已被广泛用于解决多目标优化问题。其迭代形式如下: (15) (16) 传统的粒子群算法虽然结构简单,容易实现,但是在搜索过程中存在易陷入局部最优的缺点[13],而改进后的基于混沌理论和模拟退火算法思想的PSO算法,在传统的PSO算法中引入了模拟退火算法的概率突跳思想,在寻优过程中,使算法在退火温度的控制下既可以接受好的解,也能以一定的概率接受劣质解[14],从而有效地避免了粒子过早的陷入局部最优的缺点,提高了算法的全局遍历性。 引入混沌理论对参数r1、r2随机自适应赋值,使得在搜索过程中算法中的粒子群体运动更加高效,更加优化。采用Logistic模型对r1、r2进行动态赋值,产生的混沌序列如下: (17) 本文采用改进后的粒子群算法对传感器的结构参数进行寻优。定义适应度函数如下: F(X)=α·P+β·Kc (18) 其中,α、β为权重系数,可根据优化目标的侧重点不同进行调整。传感器优化问题转化为在粒子群中寻求使F(X)取得最小值的参数组合,该组参数就是最优化问题的解。 根据传感器的固有结构以及管道容量、机械强度的要求,设置各个结构参数的取值范围为:R1∈[22,75],R2∈[24,85],R3∈[27,104],θ∈[14°,30°),h1∈(0,20)。设最大迭代次数为100,并采用训练好的RBF神经网络计算每个粒子的适应度值。 算法具体寻优过程如图7所示,经过寻优,最终得到一组使F(X)取得最小值的最优结构参数:θ=24°,d1=15.5 mmd,R2=85.5 mm,d2=14.5 mm,h1=4.6 mm,将这组参数作为混沌模拟退火粒子群算法的寻优结果。 图7 参数寻优过程Fig.7 The process of Parameter optimization 为了验证优化后的传感器性能,采用经典的LBP算法对基准传感器、正交设计优化的传感器以及混沌模拟退火粒子群算法优化的传感器分别进行图像重建。该仿真实验的硬件环境为Intel Core 2.50 GHz CPU(RAM 4.00 GB),软件环境为Matlab2017a,实验结果如图8所示。 图8 图像重建结果比较Fig.8 Comparison of image reconstruction results 为了定量分析重建图像的质量,本文通过计算重建图像的相对误差(IE)和相关系数(CC)来评估重建图像的成像效果。相对误差IE和相关系数CC分别定义如下: (19) (20) 表4 重建图像相对误差Tab.4 Relative error of reconstruction image 表5 重建图像相关系数Tab.5 Correlation coefficient of reconstruction image 对实验结果进行对比分析后可知,对于同一预设流型而言,正交试验设计的传感器重建图像的相对误差较小,相关系数较高,重建图像的精度高于基准传感器的精度,而采用RBF神经网络与改进的粒子群算法优化的传感器成像效果最佳,优于正交试验设计的结果,重建图像的相对误差最小,重建图像更加接近原型,能更好的还原管道内的真实情况。 本文采用有限元法建立了敏感场的数学模型,并对传感器的敏感场分布特性进行了分析。为了改善敏感场的软场问题,从而获得相对均匀的灵敏度分布,对传感器的结构参数进行了调整优化。通过分析影响传感器性能的各项指标,确定了传感器优化的目标函数。针对以往采用正交试验进行优化设计所存在的问题,本文在正交试验的基础上,采用RBF神经网络对正交设计的试验结果进行了回归分析,得到的预测模型能够很好的反映优化参数与目标函数之间的复杂关系,并采用混沌模拟退火粒子群算法寻优获得了一组优化参数。提出的新方法参数组合具有随机性且寻优范围大,采用优化后的传感器进行图像重建,重建图像的精度有明显的提高,对ECT系统的研究具有重要意义。

6 RBF神经网络回归分析


7 基于混沌模拟退火粒子群算法的传感器结构参数优化



8 图像重建




9 结 论

