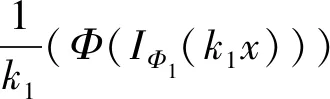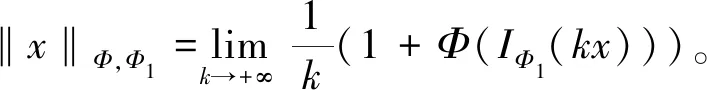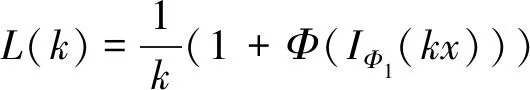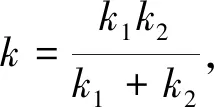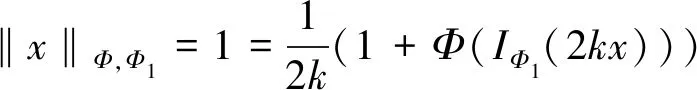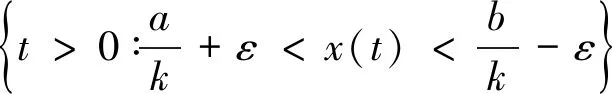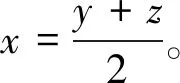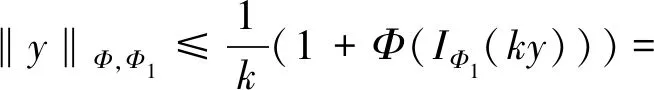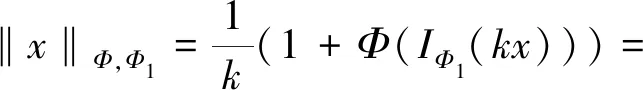赋Φ-Amemiya范数的Orlicz空间的端点

崔云安，安莉丽

(哈尔滨理工大学 理学院，哈尔滨 150080)

0 引 言

Orlicz空间作为一类特殊的Banach空间，自从1932年波兰数学家Orlicz引入Orlicz空间以来，Orlicz空间理论就因其重要的理论和应用价值受到了许多数学工作者的关注，并在微分方程、逼近论、控制论、不动点等许多数学分支学科中得到了广泛应用[1]。在其发展过程中主要出现了3个范数：1932年由Orlicz本人给出了Orlicz范数的定义[2]；1955年，Luxemburg在Orlicz空间中引入了Luxemburg范数[3]；2008年崔云安和段丽芬引入了p-Amemiya范数[4-7]。众所周知，关于赋Orlicz范数、Luxemburg范数以及p-Amemiya范数的Orlicz空间性质的研究已经比较成熟，所以对Orlicz空间的新性质的进一步研究是十分重要的[8-9]。我们将研究比上述3种范数更具有广泛意义的新范数，赋Φ-Amemiya范数的Orlicz空间的可达性、端点和严格凸性。主要给出了范数可达的充要条件和端点的判别准则，并据此得到了赋Φ-Amemiya范数的Orlicz空间严格凸的充要条件。

1 预备知识

本文以X表示一个Banach空间，B(X)和S(X)分别表示闭单位球和单位球面。

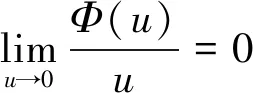
设L0表示定义在G上的可测实函数全体，

定义IΦ：L0→R+=[0,+∞)如下：

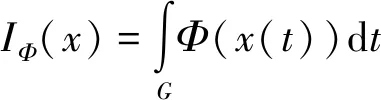
由Orlicz函数生成的Orlicz空间记为

LΦ={x∈L0:∃λ>0,IΦ(λx)<∞}

关于Orlicz范数(Amemiya范数)：

Luxemburg范数：

以及广义Orlicz范数：

均成为Banach空间[11-15]，简记为:

LΦ=[LΦ,‖·‖ΦΦ]

LΦ,p=[LΦ,‖·‖ΦΦ,p]

定义2设Φ1是N-函数，(G,∑,μ)是无原子有限测度空间，记L0(G)为G上的μ-可测函数的全体。定义模IΦ,Φ1∶L0(G)→R如下：

由Φ1及Φ是凸函数知，IΦ,Φ1为凸模，记

LΦ,Φ1={x∈L0(G)∶∃λ>0,IΦ,Φ1(λx)<+∞}

定义3设Φ是Orlicz函数，满足max{0,u-1}≤Φ(u)，在LΦ,Φ1(或EΦ,Φ1)上赋Amemiya范数，称为Φ-Amemiya范数:

利用Φ-Amemiya与Luxemburg范数等价，很容易得{LΦ,Φ1,‖·‖ΦΦ,Φ1}是Banach空间。

定义4x∈S(X)称为端点是指

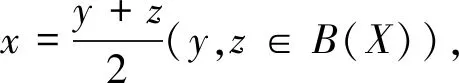
定义5称N-函数满足Δ2条件是指存在k>2，u0≥0满足：

Φ(2u)≤kΦ(u) (u≥u0)

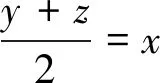
2 主要结果及证明

先引入两个记号:

|x(t)|dt-Φ(IΦ1(kx))≥1}

|x(t)|dt-Φ(IΦ1(kx))≤1}

定理1当且仅当k∈[k*,k**]时，

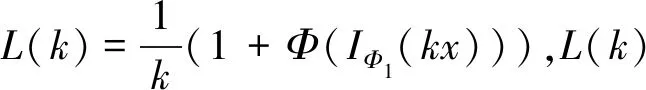
D(x)={0

取x∈LΦ,Φ1{0}，D0(x)为D(x)的内点集对∀0

所以对∀k∈D0(x)函数

按通常数学分析规则可求得：

Φ(IΦ1(kx))-1}

假设∃k0∈D0(x)使得k*≤k0≤k**，则对0

Φ(IΦ1(kx))≤1,对k∈D0(x)∩(k0,∞)

Φ(IΦ1(kx))≥1。

所以对

对k∈D0(x)∩(k0,∞),

因此当且仅当k*≤k0≤k**时

推论1若Φ1是N-函数，则

k(x)≠∅(x≠0)。

则L(k)是关于k的连续函数。

由Φ1是N-函数可得

故k(x)≠∅。

定理2若Φ1是N-函数，x∈S(LΦ,Φ1)是B(LΦ,Φ1)端点的充分必要条件是:

μ({t∈G,kx(t)∈RSΦ1})=0，k∈K(x)

2=‖y‖Φ,Φ1+‖z‖Φ,Φ1=

2‖x‖Φ,Φ1=2

即2k∈K(x)。

并且对几乎所有的t∈G都有

Φ1(2kx(t))

再由已知条件2kx(t)∈SΦ1可得，对几乎所有的t都有k1y=k2z，所以

k1=‖k1y‖Φ,Φ1=‖k2z‖Φ,Φ1=k2。

因此y=z这就说明x为B(LΦ,Φ1)的端点。

必要性(反证法)假设结论不成立。不失一般性，设k∈K(x)，μ({t∈G∶kx(t)∈RSΦ1})>0， 因为SΦ1的余集可表示为至多可列个开区间的并集,所以必存在某个开区间(a,b)，使得Φ(x)在(a,b)上是线性的，Φ(x)=px+q。并且存在ε>0，使得

将集合

由μ(E)=μ(F)>0，可知y≠z。

当t∈GE∪F时，ky(t)=kx(t)∈(a,b)。

当t∈E时，ky(t)=k(x(t)-ε)

又a

所以ky(t)∈(a,b)

当t∈F时，ky(t)=k(x(t)+ε)

又a+2kε

所以ky(t)∈(a,b) 于是

由此可得:IΦ1(ky)=IΦ1(kx)

同理可得‖z‖Φ,Φ1≤1

这与x为B(LΦ,Φ1)的端点矛盾。

定理3若Φ1是N-函数，LΦ,Φ1是严格凸的充要条件是Φ1是严格凸的。

证明：充分性由定理2立即可得。接下来证必要性。

若Φ1非严格凸，则存在x0∉SΦ1取E1⊂G，使得0<μE1<μG，且Φ1(x0)μE1≤1，Ψ1(p(x0))μE1≤1。

再取x1>0，使得

Φ1(x1)μ(GE1)≥1和Ψ1(p(x1))μ(GE1)≥1，

于是

Φ1(x0)μ(E1)+Φ1(x1)μ(GE1)≥1

Ψ1(p(x0))μ(E1)+Ψ1(p(x1))μ(GE1)≥1

即

Φ1(x0)μ(E1)+Φ1(x1)μ(GE1)+

Ψ1(p(x0))μ(E1)+Ψ1(p(x1))μ(GE1)≥2

对于Orlicz函数Φ取

Φ′(Φ1(x0)μ(E1)+Φ1(x1)μ(GE1))·

(Φ1(x0)μ(E1)+Φ1(x1)μ(GE1)+

Ψ1(p(x0))μ(E1)+Ψ1(p(x1))μ(GE1))-

Φ(Φ1(x0)μ(E1)+Φ1(x1)μ(GE1))≥1

然后选E2⊂GE1,满足

Φ′(Φ1(x0)μ(E1)+Φ1(x1)μE2)·

(Φ1(x0)μ(E1)+Φ1(x1)μE2+

Ψ1(p(x0))μ(E1)Ψ1(p(x1))μE2)-

Φ(Φ1(x0)μ(E1)+Φ1(x1)μE2)=1

令

k=1+Φ(Φ1(x0)μ(E1)+Φ1(x1)μE2)

则

Φ′(Φ1(x0)μ(E1)+Φ1(x1)μE2)·

(Φ1(x0)μ(E1)+Φ1(x1)μE2+

Ψ1(p(x0))μ(E1)+Ψ1(p(x1))μE2)-

Φ(Φ1(x0)μ(E1)+Φ1(x1)μE2)=1

但μ(t∈G∶kx(t)∉SΦ1)≥μE1>0。

由定理2得，x不是B(LΦ,Φ1)的端点，产生矛盾。