基于深度学习的“小学数学概念教学”实践与思考
张秉金 杨志宇
摘 要:人的深度学习与浅层学习相对,浅层学习是对零散的、无关联的内容不加判断的机械记忆,与学生的知识经验缺乏关联。深度学习是围绕具有挑战性的学习主题,思考数学的本质,构建知识之间内在联系的学习。深度学习是对学习内容中关键问题积极主动的理解、联系和结构的建立。通过遵循认知规律、深度学习数学概念;围绕学习主题、深度学习数学概念;把握数学本质、深度学习数学概念;构建知识结构、深度学习数学概念等方式,使学生在深度学习中得到知识技能学习与思想方法培养的有机统一。
关键词:小学数学;深度学习;概念教学
中图分类号:G623.5 文献标识码:A 文章编号:1009-010X(2021)07-0029-04
深度学习源于计算机科学、人工神经网络和人工智能的研究,这里的深度学习是机器的深度学习,不同于人的深度学习。人的深度学习与浅层学习相对,浅层学习是对零散的、无关联的内容不加判断的机械记忆,学习内容脱离学生的生活经验,与学生已有知识经验缺乏关联;而深度学习则是对学习内容积极主动的理解、联系和结构的建立。
郭华教授等人的研究成果显示,所谓深度学习,就是指在教师引导下,学生围绕着具有挑战性的学习主题,全身心积极参与、体验成功、获得发展的有意义的学习过程。在这个过程中,学生掌握学科的核心知识,理解学习的过程,把握学科本质及思想方法,形成积极的内在学习动机、高级的社会性情感、积极的态度、正确的价值观,成为既具独立性、批判性、创造性又有合作精神,基础扎实的优秀的学习者,成为未来社会历史实践的主人。
数学概念是现实对象在数量关系和空间形式方面的本质属性在人脑中的反映。学生学习数学概念就是理解和掌握一些数学对象的本质属性。学生学习数学知识的过程,实际上就是掌握数学概念并运用数学概念进行判断、推理的过程,一切数学规则都是建立在一系列概念的基础之上。因此,数学概念是数学大厦的基础,更是学生形成数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析等这些数学核心素养的基础,也是培养学生应用能力和创新能力的基础。
一、遵循认知规律、深度学习数学概念
学生对抽象的数学概念的建构,是按照“动作认知(操作水平)——图形认知(表象水平)——符号认知(分析水平)”的认知规律循序渐进地建立起来的。人们要形成正确的数学概念,需要多元的感性材料,经历从具体到表象,从表象到抽象的过程。在这一过程中,学生对数学概念由感性认识上升到理性认识,由表象深入到本质,即“从生动的直观到抽象的思维”,是学生形成正确概念的重要途径。在进行教学时,首先,要给学生提供充分而准确的感知材料,“充分”是指感性材料的数量,“准确”是指提供的感性材料要典型,强调感性材料的质量。在概念的学习过程中,教师还要注意言语的导向功能,要使“感知”成为有目的有计划的观察活动。其次,要使学生建立和获得表象,促进感知向抽象思维过渡。直观感知只是为学生提供了理解的起点,表象的建立能使学生更快地摆脱具体事物的束缚,顺利地向抽象思维过渡。第三,抽象概括一类事物的本质属性形成数学概念。教师要引导学生分析、综合与比较,再通过抽象、概括,舍弃非本质的特性,抽象出事物的本质特性,形成概念。
教学“三角形”时,上课伊始教师用课件呈现自行车支架、相机支架、斜拉桥等图片,学生观察图片中的三角形,用手描一描并说一说发现的三角形。学生汇报后,教师课件演示从图片中抽象出三角形。接下来引导学生闭上眼睛想象一个三角形,并用直尺画出来。通过展示、对比学生画的三角形,引导学生理解“围成”“每相邻两条线段的端点相连”等知识,最后抽象出三角形的概念——由3条线段围成的图形(每相邻两条线段的端点相连)叫做三角形。
教学“6的认识”时,教师课件呈现6个苹果、6名学生、6朵花等,引導学生点数。并且指出这些物体个数都可以用数字“6”表示。接下来引导学生摆出6个圆片、画出6个圆圈、找出数量是6的物体。通过数一数、摆一摆、画一画、找一找等活动,由具体到抽象再到具体,充分认识数字“6”。
二、围绕学习主题、深度学习数学概念
俗语说“提领而顿,百毛皆顺”。因此,在课堂教学中,教师要选择关键问题作为深度学习的主题。数学学科的关键问题一般指学科中的主要内容、核心内容,它是一系列相关知识串联起来的形成知识结构上的“神经突触”。关键问题不是某一具体数学知识,而是某一单元或几个相关单元一系列知识背后的数学本质、思想方法,是一系列数学知识的提炼和升华。将这样的关键问题作为深度学习的主题开展学习,在学习基础知识、基本技能的同时深刻学习其本质和思想方法。如,在教学“小数的意义和性质”这一单元时,关键问题是计数单位,我们可以把小数的意义、小数的读写、小数的性质、小数的大小比较、小数点的移动对小数大小的变化等学习内容与“计数单位”建立联系,并给“计数单位”以核心地位。本单元每一节内容的学习都围绕“计数单位”这一学习主题开展。
教学“小数的意义”时,通过人民币、米尺等多个数学模型,学生理解分母是10、100、1000……的分数可以用小数表示,小数的计数单位是十分之一、百分之一、千分之一……,分别可以写作0.1、0.01、0.001……。突出小数是十进分数的这一特征,感受学习小数的价值。
教学“小数的读写”时,学生认识数位顺序表,体会小数和整数的联系,同样采用十进制计数法,相邻计数单位之间的进率是10,启发学生感悟位值制。
教学“小数的性质和大小比较”时,在小数部分的末尾添上0或去掉0,小数的大小不变。如0.6=0.60,它们的计数单位不同,数值却相等,这背后的本质是计数单位和对应的个数同时变化。0.6里面有6个十分之一,0.60里面有60个百分之一,6个十分之一和60个百分之一相等,所有0.6=0.60。
小数点位置移动引起小数大小变化教学时,小数点向左移动一位,相当于这个数除以10;小数点向左移动两位,相当于这个数除以100……。小数点向右移动一位,相当于这个数乘10;小数点向右移动两位,相当于这个数乘100……。小数点的移动引起小数大小变化,其本质是计数单位变了,而计数单位的个数没有变。如,0.65小数点向右移动一位是6.5,0.65里面有65个百分之一,6.5里有65个十分之一。0.65的小数点向右移动一位,计数单位由百分之一变成了十分之一,而计数单位的个数不变,都是65个。
抓住这个单元中的关键问题——计数单位,系统设计整个单元的教学程序,将单元教学目标分解到每个课时,才能在每个课时的教学设计中围绕“关键问题”有计划地进行渗透、有目的地进行点拨,让学生有机会围绕不同内容,在多层次、多视角的探究中,不断加深对小数意义的理解。准确把握单元教学的“关键问题”设计主题学习,是深度学习开展的基础。
三、把握数学本质、深度学习数学概念
小学数学所涉及到的数学概念是最简单、最基本的,但都是非常重要的。“最简单的往往是最本质的”,发生深度学习的学生能够抓住教学内容的本质属性,深刻理解相关数学概念。把握本质的过程就是去除非本质的干扰、分辨本质和非本质属性区别的过程。而深刻理解概念的内涵,感悟其数学思想是学生对数学概念深度学习的重要标志,也是学生思维成长的必经过程。
如教学“方程”时,教师引导学生从生活情境中抽象出等量关系,用语言描述等量关系,再用等式表示出它们的关系,让学生深入理解等式,在此基础上,学习方程的概念。如,在教学方程时创设篮球比赛情境,出示篮球比赛红队和蓝队比分32:39。
师:现在场上的状态是什么样子的?
生:红队比分落后。
师:你能用式子表示吗?
生:32<39。
师:红队教练换上主力队员,连得几分,可以怎么表示呢?
生:可以用x表示。
师:红队现在的得分是多少?
生:32+x。
师:蓝队没有得分,他们的得分还是39。
师:现在场上两队的分数谁领先呢?
生:可能红队领先,可能蓝队领先,还可能两队得分相等。
师:得分相等的时候用哪个式子表示呢?
生:32+x=39。
方程是学生用代数思维分析现实生活中等量关系的重要载体,是学生后续数学学习的重要基础。方程的教学不能仅停留在记忆概念的浅层学习,要结合生活情境,经过发现等量关系,用语言描述等量关系,用含有未知数的等式表示等量关系的全过程。
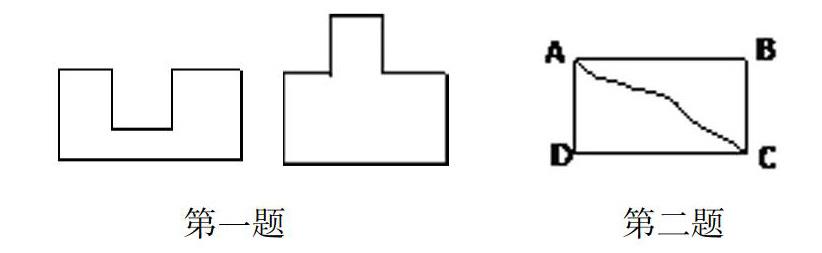
再如教学“周长”时,学生初次学习周长,往往是感性的、直观的,认为图形的形状、大小一样,周长才会相等。为了能够让学生更加注重周长本质的理解,课堂教学时,教师呈现了如下素材。
第一题中两个图形形状不同,凹字形和凸字形的周长是一样的。第二题图形ADC和图形ABC的形状不同,但周长相等。通过上面这样两组习题的对比,更加凸显周长的数学本质。
四、构建知识结构、深度学习数学概念
皮亚杰认为:“人的认识总要形成整体的心理构造,这种心理构造是在不断的认识活动中建造起来的,即有一个发生、更新和改造的进化过程,心理的整体构造能使人的思想更加完善,并且是获得更高知识的有效工具”。数学概念也有类似整体结构的性质。一个数学概念它从一些最基本的概念中得来,又为建立新的概念做基础,从本质上说,每一个概念都是嵌进了一些概念的体系当中,是这个体系中的一个“细胞”。因此理解一个数学概念,不仅要理解概念本身的规定,而且要从它在整个概念体系的位置以及和其他概念的关系中去理解。深度学习中对概念的理解,教师必须引导小学生对已经掌握的概念不断更新、改造、组织、整理,将零散的知识结构化,形成有序的概念体系,从整体上去把握概念之间的有机联系,以抓住本质属性。
教学“百分数”时,学生学习了百分数的意义,理解了它表示两个数之间的关系,再引导学生思考,表示两个数的关系还可以用分数、倍和比表示,通过下面的练习对比这几种数学概念的异同,凸显出学习百分数的价值。
下面哪些是可以改写成百分数表述的?
1.鸡蛋的蛋白质含量是,一个鸡蛋重千克;
2.一家超市周六的销售额是周五的2倍;
3.青少年体内水分与自身体重的比是70:100。
第1题中两个分数,第一个分数表示关系可以用13%表示,第二个分数表示具体的量,不能用百分数表示;第2题中的“2倍”表示周六与周五销量的关系,所以可以改写成一家超市周六的销售额是周五的200%;第3题中的比表示两个量之间的关系,也可以改写成青少年体内水分占自身体重的70%。
通过这样的比对,不仅强化了百分数的意义,而且引发学生关于学习百分数的价值,凸显出百分数在统计时便于比较大小的优势。
教学“负数”时,在学生初步认识了负数的基础上,引导学生对比之前学过的整数、分数,发现在它们前面加上负号就是负数,小学阶段学过的数可以分为正数、0、负数,负数也有整数和分数的不同形式。通过深度学习既扩展了数域,又了解了小学期间学习的各种数之间的关系。“负数”一课学生还学习了0的新含义,0既不是正数也不是负数,它是正数和负数的分界线。在学生理解了这一知识后,教师引导学生回顾0的其他作用——0可以表示没有,表示占位,表示测量的起点等。通过与学生已有知识经验对比,在学生头脑中建构数的知识结构,为学生在中学继续学习数的概念打下基础。
教师在学生的深度学习中仍然发挥著组织者、引导者、合作者的重要作用,没有教师,虽然学生也会学习,但离开教师的组织、引导、合作,很难发生深度学习。“学然后知不足,教然后知困。”没有教师巧妙地创设教学设计,很难有学生深度学习的发生;反过来,在不断引发学生深度学习的思考过程中,教师的专业技能也得到了持续发展。
在深度学习中,教师与学生,知识技能的学习与思想方法的培养等不再是分离的、对立的,而是有机统一的。数学概念教学活动的设计能够遵循儿童的认知规律,准确把握关键问题并形成单元学习的主题,剖析数学的本质,建构知识的联系,形成知识结构,在课堂教学中关注学生的学习,深度学习才会发生。
参考文献:
[1]马云鹏,吴正宪.深度学习:走向核心素养(学科教学指南·小学数学)[M].北京:教育科学出版社,2019.
[2]刘月霞,郭 华.深度学习:走向核心素养(理论普及读本)[M].北京:教育科学出版社,2019.
[2]张奠宙,唐瑞芬,刘鸿坤.数学教育学[M].南昌:江西教育出版社,1991.
[4]张兴华.儿童学习心理与小学数学教学[M].南京:江苏教育出版社,2011.

