巧用变式教学 培育初中生数学核心素养

董彬

（福州第二十五中学，福建 福州 350009）

目前我国正处于一个教育教学方式转型、改革和发展时期，传统的教学方法的不足日益显现。随着我国新课程改革的深入，对初中生的数学核心素养提出了明确的要求，不仅要让学生了解和掌握数学知识和技能，而且在教学过程中更要注重对学生兴趣的启发、学习思维方法的引导，鼓励学生进行创造性思维。教学实践证明，有效地进行变式教学可以引导学生主动参与教学活动，在获取所学知识的过程中，激发他们浓厚的求知欲和创造力，从而提高数学课堂效率，培养学生发散、化归、逻辑、创造等综合思维品质，从而促进学生通过变式教学培养数学学科的核心素养。

一、数学变式教学的概念

变式教学是一种在教学过程中运用不同的知识和手段，对有关数学概念、公式、定理、习题等进行不同角度、不同层次、不同背景下的变化，通过有意识地引导学生从“变”的现象中发现“不变”的根源，从“不变”中寻找并探求规律，最终目的是通过变化让学生掌握变化中的不变，从而概括出事物的普通属性，使学生能够在真正理解知识和方法的基础上掌握其本质和原理的教学方法。它的核心在于利用一系列的问题与变式，向学生展示知识的产生、发展、变化的过程，揭示数学问题的结构和变化过程，暴露解决问题的思维过程，从而建立起一种科学的思维培养训练的有效方法。

二、当前初中变式教学存在的问题

首先，大多数数学教师只是将变式教学作为一种教学手段，更多关注例题变式的解题，对变式题目的设计与使用大多处于较低的水平，变式教学成为一种空有形式的教学；同时，学生没有积极、主动地参与变式教学的学习之中，变式训练仅仅停留在做题的层面，没有引导学生对问题的本质进行深入的探究和思考，无助于学生拓展思维；其次，教师没有从教学的方式、策略、途径的层面思考及认识变式教学，不能很好起到锻炼学生的目的。主要存在脱离学生的认识基础和能力，跨度太大，学生跳一跳也够不着；变式没有循序渐进、跳跃性大；没有突出重点、导致重心跑偏，与教学的重难点内容不是很匹配。同时变式主线不明，变量多且庞杂，没有理出变式的主要线索，没有突出主要问题，抓主要矛盾，难度过大，大部分学生完全摸不到头绪，导致学生丧失学习数学的积极性，效果反而更差。

三、变式教学有效运用的策略

（一）变式设计需体现差异性

变式教学不是让学生简单机械地重复训练，否则将会降低学生思考问题的积极性。心理学研究表明：题目的新颖度越大越容易刺激学生的感官和兴趣，越容易使其保持注意力的集中与思维的敏捷，教学的效果越好。因此，在变式设计时选择的题目应该要有新颖性，便于调动与激发学生的好奇心和求知欲。这就要求教师在设计变式习题时题目之间应具备明显的差异。

例如，在初中七年级上“利用等式的性质2 解一元一次方程”的教学中，教学过程中设计如下变式题目，得到的教学效果是无效的。

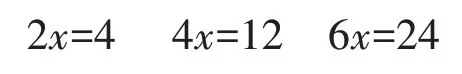
以上三个方程结构过于类似与接近，学生训练此类题目无异于简单的重复，意义不大。但是加上符号的变化，改成如下三个方程就大为不同。

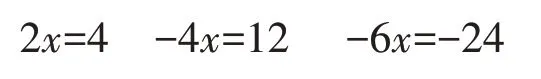
经过符号变化之后，虽然解题的依据仍是等式的基本性质2，但各方程之间具备了明显的差别，更有利于学生掌握该性质。

如果再进一步做出如下的变式将会更加有效：

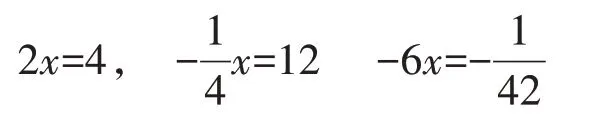
经过这样的变式后，学生将会同时应用到等式基本性质2 和有理数除法运算两个知识点，实现新旧知识的相互渗透。

（二）变式设计需体现层次性

变式教学在题目设计过程中，还要特别注重题目的层次递进性，通过有目的、有意识地启发引导学生在不断的变式过程中，发现“不变”的原因和本质，从“不变”的本质中寻找规律，使学生充分获得思维活动的点点滴滴经验，提高解题能力，从而达到强化学生思维训练的目的。

例如，在引导学生掌握全等三角形在解题中的应用时，可呈现课本上的例题：

如图所示，四边形ABCD 是正方形，其中点E 为边BC 的中点，∠AEF=90°，EF 与正方形外角平分线相交于点F，试证明：AE=EF

本题可以取M 为AB 的中点，连接EM，即可构造一个ΔAEM；只需证得ΔAEM≌ΔEFC，从而完成题目的证明。对此例题可做如下的变式：

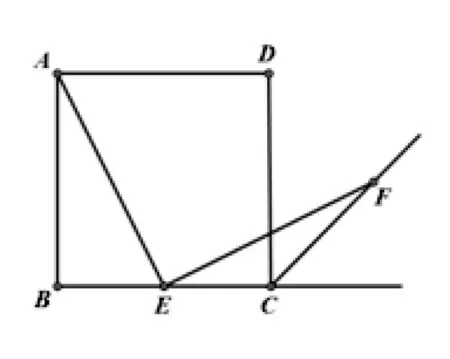
变 式1:如 果 点E 不是BC 中点，AE 和EF 有何关系？

此变式需要引导学生进行三种情况的分类讨论：点E 在BC 上、点E 在BC 延长线上和点E 在CB 延长线上。解题思路还是要构造全等三角形。

变式2：如果把正方形换成正三角形，如图所示，且∠CEF=60°，结论是否仍然成立？

通过类比证明，结论仍然成立。

变式3：如果把正方形换成正六边形，又会得到什么结论？

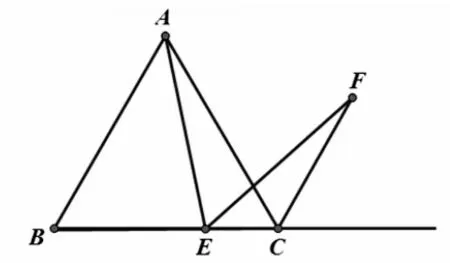
变式4：如果把正方形换成正n 边形，又会得到什么结论？

变式5：如果把正方形换成正n 边形，当∠CEF=__________时，结论AE=EF 仍成立？

以上五个问题的变式条件各不相同，但最终结论仍然是一致的。学生通过层层递进的例题变式，感受数学题目充满了无穷变化，提升了学习兴趣。

（三）变式设计应具内涵性

变式教学中所选取的问题应该具备典型性，体现不同知识点之间的横、纵向联系，要有一定的内涵，给学生预留充裕的思考空间，让学生体验各种数学思想方法，并获得思维品质与素养的提升。

例如，在二元一次方程组的加减法教学中，当学生对加减法有了初步的了解，可以提供以下的方程组：

当学生通过解题形成用加减法求解二元一次方程组的数学结构时，可以用含字母系数呈现二元一次方程组：

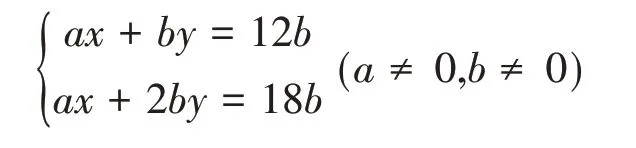
学生在反思之后，就会紧紧抓住用加减消元法解二元一次方程组的特点，认识并找到解题的根本关键是看方程组中的系数是不是相同，或者是不是互为相反数，或者能不能通过方程变形得到相同或者互为相反数的系数，这就是用加减消元法解二元一次方程组的本质。学生理解了这一点，原有的数学结构框架就能得到拓展与提升。

四、实施变式教学应注意的问题

（一）注意与现代教育技术应用相结合

当下，信息技术已经成为初中数学课堂教学不可忽视的重要工具，多数学校安装了电子白板或触屏等多媒体设备，信息技术已经真正进入课堂。在教学中，变式教学过程可以与现代教育技术相结合，更好地发挥变式教学的作用，形成更有效的教学模式。现代信息技术既可静态展示几何图形结构或是函数图像，又可以动态展示图形或图像的变化过程，比传统的教学更容易调动和激发学生学习积极性，使学生对相关知识形成清晰、深刻的理解和认识，能收到更好的课堂教学效果。

（二）注意引导学生在变式中学会探究

在变式教学过程中，教师要想更好地发挥变式教学的优势，取得更好的教学效果，要引导学生对变式问题的对应情境自主展开研究。数学教学过程既是学生主动探究的过程，也是师生之间进行交流合作的过程，教师要重视学生对数学知识探索的过程，可先引导学生独立完成较为容易的数学问题，通过交流和讨论，共同分析疑难问题，找到解决问题的方法，学生在自主探究的过程中，逐渐形成系统化的知识体系和数学方法，将会使教学质量和效率大大提高。

（三）注意利用变式启发学生学会思考

在变式教学过程中，教师要引导学生对所要解决的数学问题产生一系列思考，并通过从特殊到一般的变化，不断深化思考层次，帮助学生把握问题的本质。启发学生对这些变式问题之间的内在联系进行思考，提炼并总结出解决问题的途径与方法，使学生在原有的认知基础上获得提高，从而增强学生解决实际问题的意识与能力。

（四）注意变式程度需要做到适合学生水平

在实施变式教学的过程中，为了达到预期的教学效果，必须根据所教学生的数学认知水平，选择最为合适的变式问题。设置的问题既要有梯度，做到由易到难，逐步深入；也不应该跨度太大，超越学生的接受水平。变式教学的效果如何，不在于变式生成的问题的数量，而在于所生成问题是否典型，是否有利于学生对概念的理解，是否有助于学生进一步思考和解决问题，提升学生的思维水平。

实践证明，数学变式教学是提高学生基本数学技能和数学素养的有效途径，它有利于增强并提高学生思维的发散力、创新力、深度和灵活性。因此，在数学教学中，广大教师要善于运用变式教学开展教学活动，充分利用典型例题来对其进行演变、探究、引申、拓展、应用，由点到面，由题及类，解剖一例，带活一类。同时，教师要做好变式教学应用的研究，掌握变式教学的应用技巧，采取具有针对性的教学策略，促进变式教学优势得以充分发挥，促进课堂教学效率和学生数学素养的提高。