固定机械结合面法向接触刚度分形模型*
谭文兵,兰国生,张学良,孙 万,温淑花,陈永会
(太原科技大学机械工程学院,太原 030024)
0 引言
机械结构中结合面不仅分布广泛,而且起着重要的作用,尤其在各种高精密设备中,结合面接触刚度对整机的精度和性能有重要影响,有研究表明,机床60%~80%刚度[1],来自结合面,而机床总刚度直接影响着零件的加工精度。可见,对结合面接触刚度的研究意义重大。
对于机械结合面接触刚度的研究,文献[2]应用分形理论,首次提出了尺度独立的结合面法向接触刚度分形模型。文献[3]结合修正的W-M函数,建立了考虑域扩展因子影响的结合面法向刚度改进模型,之后人们对结合面接触刚度模型做了进一步的研究[4-6],然而均未考虑结合面微凸体的弹塑性变形,仅考虑了微凸体的弹性和塑性变形。文献[7]提出了考虑微凸体弹塑性变形阶段影响的结合面刚度模型,并分析了相关因素对结合面刚度的影响,然而存在的问题是,该模型微凸体弹塑性变形阶段的变形机制是以插值法得到,不能准确表达该阶段的真实规律,且与文献[8]得到的结果存在一定的误差。文献[9]应用文献[8]的研究成果,建立了考虑微凸体弹塑性变形影响的结合面刚度统计学模型。文献[10-12]应用文献[8]的研究成果,分别提出了考虑微凸体弹塑性变形影响的结合面法向刚度二维分形模型和切向刚度分形模型,以及结合面法向刚度三维分形模型,并通过仿真得到了相应的结论,但是均未充分考虑微凸体弹塑性接触变形阶段接触载荷和接触刚度与接触面积间的力学关系。此外,文献[13]基于结合面基本分形理论,对结合面微凸体弹性接触变形阶段法向刚度的计算存在问题,主要体现在法向刚度的计算过程中:对于MB分形模型,忽略了结合面上单个微凸体在法向上的压缩变形过程,而在横向上表现为微凸体间不断融合形成更大的微凸体,即目标接触点接触面积在横向上不断融合增大,从这里可以看出,文献[13]中计算得到的弹性阶段刚度的理论计算并不是单个微凸体上的法向刚度。文献[12,14]也存在同样的问题。
鉴于此,基于结合面基本分形理论,应用极限的思想,对结合面单个微凸体弹性阶段法向刚度进行修正;基于文献[8]的研究成果,应用结合面基本分形理论,考虑了单个微凸体弹塑性变形阶段接触载荷、接触刚度与接触面积间的力学关系,对该阶段单个微凸体法向载荷以及法向刚度算法进行了改进,进而建立了结合面法向接触刚度分形模型。通过与实验数据进行对比,表明所建模型能较好的预测固定结合面静刚度。
1 微凸体的接触变形
1.1 微凸体弹性接触变形阶段
图1为结合面微凸体与刚性平面接触前后变形示意图,微凸体处于弹性接触状态时,变形量为δ,接触面积a以及接触载荷pe的关系为:
a=πRδ
(1)
(2)

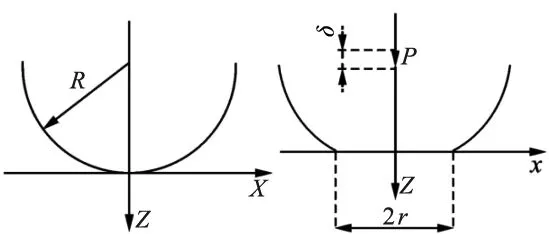
(a) 接触前 (b) 接触后 图1 理想刚性平面与微凸体接触
1.2 微凸体弹塑性接触变形阶段
微凸体弹性临界变形量为[15]:
(3)

当微凸体变形量δ>δc时,开始出现屈服现象。研究结果表明[8],在δc≤δ≤110δc,微凸体发生弹塑性变形,细分为两个区域,对应的变形量,微接触面积以及载荷间的变形机制为:
当δc≤δ≤6δc时
(4)
(5)
当6δc≤δ≤110δc时
(6)
(7)
1.3 微凸体塑性变形阶段
当δ>δp=110δc时,微凸体处于塑性接触状态,微接触面积与载荷为:
a=2πRδ
(8)
pp=2πRδH=Ha
(9)
2 结合面基本分形理论
结合面微接触点的面积密度分布函数为[16]:
(10)
(11)
此时微凸体变形量为:
(12)

(13)
2.1 微凸体弹性接触变形阶段法向刚度修正算法
图2为微凸体已发生变形的轮廓,对于接触长度为l(或者说接触面积为a)的微凸体,其任意时刻的变形量δu与接触面积au的关系可表达为[17]:
(14)

(15)
则当接触面积为a时,法向接触刚度为:
(16)
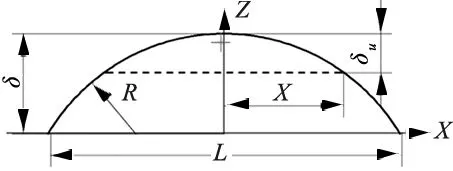
图2 微凸体的变形轮廓
可见经修正算法得到的结合面单个微凸体的法向接触刚度与经典弹性赫兹接触理论得到的相统一,即与式(2)对变形量的求导结果一致。则由式(1)、式(16)可得,当接触面积为a时,结合面微凸体弹性接触变形阶段法向接触刚度为:
(17)
由式(1)、式(2)、式(11)可得当接触面积为a时,法向接触载荷为:
(18)
2.2 微凸体弹塑性阶段法向载荷和刚度改进算法
2.2.1 弹塑性接触变形第一阶段法向载荷的计算
将式(4)代入式(5)得:
(19)
进而将式(3) 、式(11)、式(12)代入式(19)得微凸体弹塑性一区法向接触载荷分形表达式为:
(20)
这里需要说明的是,基于文献[8]提出的分形模型[10-12]均未考虑单个微凸体在弹塑性接触变形阶段其法向载荷与接触面积间的关系,即式(4)与式(5)。本文考虑了法向载荷与接触面积间的关系,基于式(19),进而得到单个微凸体弹塑性接触变形第一阶段法向接触载荷分形表达式。与文献[10-12]对应表达式不同,在各个参数的指数上相区别。
2.2.2 弹塑性接触变形第一阶段法向刚度的计算
由式(5)得:
(21)
将式(4)代入式(5)得:
(22)
进而由式(3)、式(11)、式(12)可得弹塑性一区接触刚度分形表达式为:
(23)
基于文献[8]提出的结合面法向刚度分形模型[10,12]未考虑单个微凸体在弹塑性接触变形阶段其法向刚度与接触面积间的关系,即式(4)与式(21),在此考虑了法向刚度与接触面积间的关系,基于式(22),进而得到单个微凸体弹塑性接触变形第一阶段法向接触刚度分形表达式。与文献[10,12]对应表达式不同,可在各个参数的指数上加以区别。
2.2.3 弹塑性接触变形第二阶段法向载荷与法向刚
度的计算
弹塑性第二阶段法向载荷及法向刚度算法类同弹塑性接触变形第一阶段。将式(3)、式(6)、式(11)、式(12)代入式(7),得微凸体弹塑性接触变形第二阶段法向载荷为:
(24)
由式(3)、式(6)、式(7)、式(11)、式(12)可得微凸体弹塑性接触变形第二阶段法向刚度为:
(25)
3 结合面法向接触刚度模型
结合面实际总接触面积为:
(26)
将式(10)代入式(26)得:
(27)
结合面总法向接触刚度为:
(28)
将式 (10)、式(17)、式(23)、式(25)代入式(28)得:

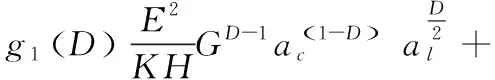
(29)
结合面总法向载荷为:
(30)
将式(9)、式(10)、 式(18)、 式(19) 、式(24)代入式(30)得:
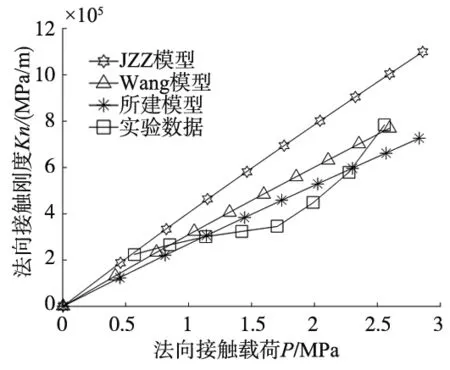
当1 (31) 当D=1.5时 (32) 将式(29)、式(31)、式(32)无量纲化得: (33) 当1 P*= (34) 当D=1.5时 (35) 式中, g4(D)= 由式(34)、式(35)可见:本文模型中处于弹塑性接触变形第一、第二阶段的微凸体总载荷以及塑性接触阶段总载荷表达式形式统一;由式(33)可见:处于弹塑性接触变形第一、第二阶段的微凸体总刚度表达式形式统一,这与文献[10-12]模型对应关系式相区别。 采用文献[6]中的实验进行验证。构成结合面的上下接触粗糙面材料均为灰铸铁,无润滑介质,材料弹性模量E1=E2=130 GPa,泊松比为v1=v2=0.25,材料硬度为H1=H2=231 MPa。表1和表2分别为粗糙表面参数和等效粗糙表面参数。 表1 粗糙表面参数 表2 等效粗糙表面参数 (a) 结合面l理论与实验刚度值 (b) 结合面2理论与实验刚度值图3 模型与实验数据对比 图3为配合接触对1和配合接触对2的理论预测值与实验值的对比结果,可见,模型预测值和实验数据趋势相同,总体上,相较于JZZ模型[14]和Wang模型[6],所建模型预测值与实验值更为接近,对结合面接触刚度的预测得到了一定的提高。对于配合接触对1,如图3a所示,当法向载荷小于1.136 MPa时,理论预测值小于实验值,当法向载荷大于1.136 MPa时,理论预测值大于实验值。对于配合接触对2,如图3b所示,当法向载荷大于1.136 MPa且小于2.273 MPa时,理论预测值大于实验值,当法向载荷小于1.136 MPa且大于2.273 MPa时,理论预测值小于实验值。本文模型未考虑结合面微凸体间的相互作用、摩擦因素是造成误差的重要因素,因此有待做进一步完善。 基于结合面基本分形理论,通过对结合面单个微凸体弹性阶段法向刚度以及对结合面单个微凸体弹塑性接触变形阶段的法向载荷以及法向刚度的改进,建立了包含弹性、弹塑性、塑性三种变形机制的结合面法向接触刚度分形模型。所建模型预测值与实验值的对比结果验证了理论改进算法的有效性,所建模型能较好的预测结合面法向接触刚度。 所建模型没有考虑结合面间的润滑介质,且润滑介质对结合面接触刚度存在显著影响,所以模型不适于预测有润滑介质存在的情形。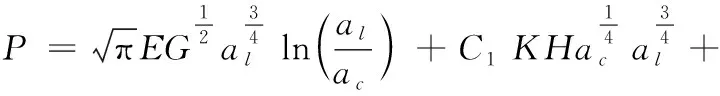


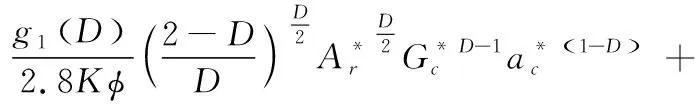





4 模型的实验验证



5 结论

