基于小波分解与深度学习的液压泵泄漏状态识别*

陈军江，陈里里,2,王朝宇

(1.重庆交通大学机电与车辆工程学院，重庆 400074；2.重庆市勘测院 ，重庆 400074)

0 引言

液压系统作为现代机械系统的主要组成部分，因其较快的响应速度、大的功率质量比、较小的体积、较高的控制精度与运行平稳的特点在机械行业得到了广泛的应用[1]。液压泵作为液压回路的核心部件，其工作状态的好坏严重影响整个机械系统的稳定。由于液压系统的高度复杂性与非线性，液压回路中故障的机理与失效形式多种多样，故障的有效特征的提取也具有很大的难度。于是提取液压信号的有效特征并完成高精度故障类别识别具有很大的研究意义。

目前，液压系统的故障识别主要借助了机械系统故障诊断的方法。一般的机械系统故障诊断方法主要从时域、频域与时频域方面对信号特征提取进行识别[2]。液压系统是一个高度复杂非线性系统，其信号是一个典型的非线性、非平稳信号，并且在液压泵工作的过程中常伴有强烈的机械振动等噪声干扰，这使得对液压信号的特征提取与识别变得异常困难[3]。针对液压信号的复杂性，目前对液压故障的主要处诊断方法基于小波分析方法、经验模态分解方法与小波包谱分析等方法[4]。唐宏宾等[5]提出了基于经验模式分解和包络谱分析的识别方法，提取了液压泵的早期故障的有效特征，精准实现了液压泵4种状态的分类。曹斌等[6]使用小波包对液压信号进行消噪预处理，然后使用小波包对信号进行分解与重构，提取频带能量作为液压信号的特征进行了有效的故障类别分类。韩可等[7]采用了变分模态分解和支持向量数据描述相结合的识别评估方法，完成了轴向柱塞泵故障的分析。王武[8]将液压信号进行了三层小波包分解,获得了8个频段的能量信号,并以此作为随机森林网络的输入进行了液压故障的分类。

然而上述方法中，只使用到液压信号的时域或者频域单一方面的特征信息，并且将计算得到的特征数据直接输入到分类模型中。这样的简单特征对于复杂的液压信号来说，不能很好地反映液压信号的全部信息。

强鲁棒性的特征与有效的识别模型对于液压信号的状态识别都至关重要。近年来，深度学习发展迅速，并广泛运用于各行各业。基于‘autoencoder’网络的堆栈稀疏自编码神经网络，是一种无监督的学习算法，能够从输入的原始数据中自动学习鲁棒性更强的高阶特征。王黎阳等[9]利用Hilbert包络谱信号输入堆栈稀疏自编码，完成了电机故障的诊断。Chen等将Softmax分类器和稀疏自编码网络应用于人机交互中的面部情绪识别。Kemal Adem等使用稀疏自编码和Softmax分类器完成宫颈癌的诊断。正是由于堆栈稀疏自编码器良好的特征学习与优化能力，其被广泛应用于故障诊断中。

本文选择液压信号中的压力与流量两类信号，对其进行时域分析并进行小波分解提取时域与小波特征作为低阶特征。然后将组合特征输入构建的堆栈稀疏自编码网络学习高阶特征，最后使用Softmax层进行液压泵的状态识别。本文使用到了液压信号的多方面的特征信息，并且通过深度学习学习了信号的高阶特征，既使特征中既包含了更全面的信息，又达到了比较好的识别效果。

1 特征提取

小波变换是对信号按照Mallat提出的塔式计算方法对信号进行计算，可以得到信号的时频信息[10]。由于本文所使用得液压信号是离散信号，所以采用离散小波变换对信号进行处理。离散小波变换的表达式如下所示：

(1)

逆变换的公式为：

(2)

在式(1)与式(2)中，f(t) 表示原始液压信号，ψ(t) 为小波母函数，2j与2jk分别表示伸缩因子与平移因子，式中A为与液压信号无关的一个常数。

本文使用db1小波函数对液压信号进行5层小波分解，每层都只对低频部分进行分解，高频部分则不处理，最后得到5个高频系数和一个低频系数，然后计算5个系数的样本熵，小波分解后系数的样本熵作为小波特征。样本熵的具体原理参考文献[11]。

为了获得液压信号所包含的更多信息，除了小波特征，本文还提取了信号的12个时域特征，分别是均值、方根幅值、均方根值、最大值、标准差、偏斜度、峭度、峰值因子、裕度因子、波形因子、脉冲因子、方差。最终将6个小波特征与12个时域特征组合作为液压信号的表征特征向量。

2 深度神经网络

本文构造的三层深度神经网络(DNN)由两个稀疏自编码器(spare autoencoder, SAE)和一个Softmax分类器堆叠而成，如图2所示。第一个稀疏自编码器的输入为低阶的小波与时域组合的特征向量，输出为优化后的特征，这些高级特征继续被接受为第二个稀疏自编码器的输入，继续对特征进行优化，第二稀疏自编码器的输出比第一稀疏自编码器的输出更高级。通过两层的SSAE对低阶特征进行优化后，堆叠在第二个稀疏自编码顶部的Softmax，用于接收第二个稀疏自编码器的输出并完成液压泵状态的识别。为了优化提出的深度神经网络的识别效果，本文使用代价函数来对整个神经网络进行微调。通过反向传播算法的使用，来调整神经网络中的Softmax层，第二层SAE，第一层SAE的参数，使得整个网络的训练误差变小，达到优化网络识别效果的目的。

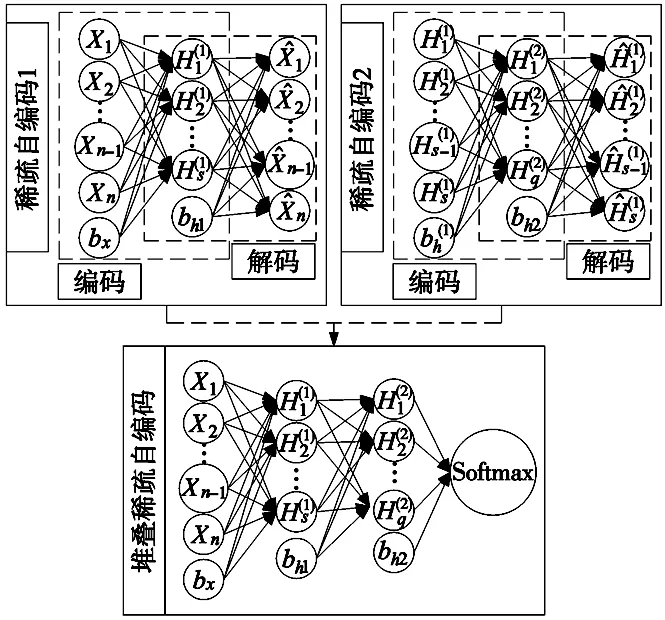
图1 识别网络结构图

2.1 稀疏自编码器

作为自编码器(autoencoder, AE)的扩展，稀疏自编码器可以通过在自编码器中引入稀疏惩罚，以非监督模式的方式学习相对稀疏的特征[12]。该方法提高了传统自动编码器的性能，在实际应用中具有广阔的应用前景。

如图2所示，一个标准的自编码器包括一个编码器和一个解码器，即一个输入层、一个隐藏层和一个输出层，它们都试图学习隐藏层的近似值，在对数据的编码与解码过程中，通过最大限度地减小原始数据与重建数据之间的差异，以便在输出层完美地重建原始数据[13]。其中隐藏层的输出可以作为未标记数据的高级特征。设未标记的特征数据为xi(i=1,2,3...N)，编码过程将输入矢量xi转化为隐藏层矢量hi，隐藏层的数据hi可表达如下：

(3)

式中，F(.)表示编码激活函数，W1和b1分别表示编码过程中的权重矩阵与偏置矩阵。

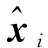
(4)

式中，F(.) 表示解码过程中的激活函数，W2和b2分别表示解码过程中的权重矩阵与偏差矩阵。值得注意的是重构后的数据与原始输入的数据是非常接近的，或者说重构数据是对输入数据的复刻，这样解码后的隐藏层数据就可以作为高阶特征使用。重构误差可表达为：

(5)

式中,N为输入的液压信号的数量，λ是用来防止过拟合的正则化参数，L和nl分别表示SAE的第L层和第L层的第n个神经元。

在此基础上，通过对自编码器的目标激活引入稀疏约束来实现特征的稀疏表示，从而形成了自编码器的稀疏约束，更好地表达输入数据。这时，隐藏单元的维数可以大于输入的维数，这称为稀疏自编码器(sparse autoencoder, SAE)。于是稀疏自编码器的重构误差可由下式计算:

(6)

式中,

(7)

(8)

在训练稀疏自编码器的过程中，利用反向传播算法来最小化损失函数来，从而得到SAE训练过程中的权重与偏置的最优参数。每次迭代的权值和偏置如下：

(9)

(10)

在式(9)和式(10)中，i和j分别表示SAE相邻两层中的第i个和第j个神经元；l表示SAE的第l层；η表示学习率。

2.2 Softmax分类器

Softmax是逻辑斯蒂回归在分类问题的扩展，在本文中，将Softmax连接到两个稀疏自编码器的顶部进行分类任务，并对整个网络进行微调[14]。作为一个二元分类器，Logistic回归定义如下:

(11)

式中，θ是模型参数，x是输入的数据。

设有m个样本{(x1,y1),(x2,y2),…(xm,ym)} ，xi为输入的特征数据，yi为相应的标签。其中yi∈{1,2，3...k} ，k为分类的类别种类数量。于是，对于每一个输入的样本xi，都将会有相应的1概率输出p(y=j|x) 来表示xi被判别为j的概率。比如，一个k分类问题，输出结果就是一个k维矢量：

(12)

Softmax的代价函数如下：

(13)

(14)

上两式中，l(.)表示指示函数，即l(真)=1，l(假)=0。

本文方法的具体流程如图2所示。

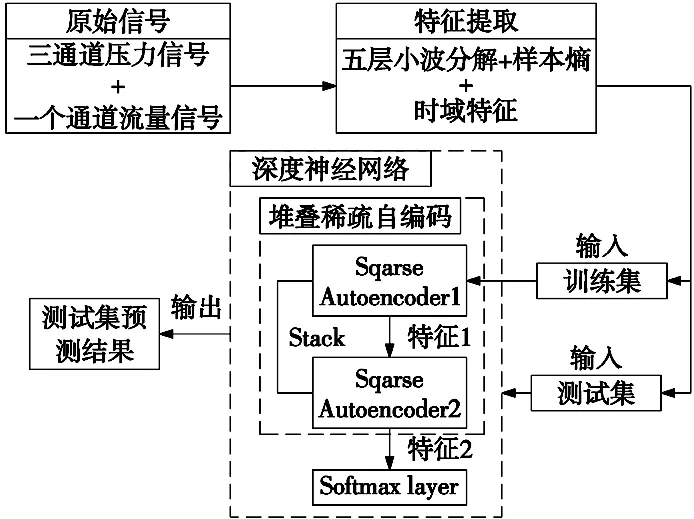
图2 本文方法流程图

3 实验与分析

3.1 数据描述

本文所使用的实验数据来自2018年公布在UCI数据库中的液压系统状态监测数据集[15]。该数据集是使用液压试验台通过实验获得的。该液压系统周期性地重复恒定的负载循环(持续时间为60 s)，在负载过程中测量过程值，包括压力、体积流量、和温度等。本文的主要研究内容为液压泵的泄漏状态的识别，故选择了与液压泵的工作状态联系比较紧密的主回路中的4个传感器的数据对液压泵无泄漏、弱微泄漏和严重泄漏三种状态进行识别。传感器包括3个压力传感器：PS1、PS2、PS3，一个流量传感器：FS1。其中3个压力传感器是按照100 Hz进行采样的，流量传感器按照10 Hz进行采样，所以一条压力传感器记录具有60 000个数据点，一条流量传感器具有6000个数据点。所使用的液压泵数据的泄漏状态、样本数量与分类标签如表1所示。

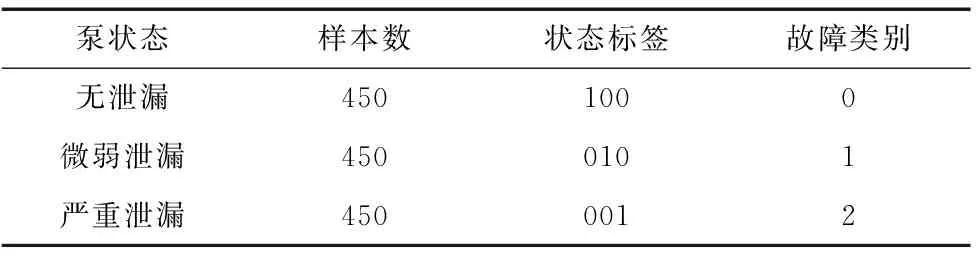
表1 液压泵样本数据

3.2 实验步骤

本文的实验流程具体步骤如下：

(1)利用小波变换与时域分析对每条记录提取一共18个低阶特征。因选择4个传感器的数据，经过特征提取，组合4个传感器的特征，所以最后使用48个特征数据来表征一种泵的泄漏状态；

(2)每类泄漏状态各有450个样本，随机选择每类状态的250个样本作为训练集，200个样本作为测试集，故最终训练集样本量为750，测试集样本量为600；

(3)对训练集与测试集建立对应标签，具体见表1；

(4)参数初始化。设置第一个SAE的隐藏层神经元个数为25，第二个SAE的隐藏层的神经元个数为8，L2正则化权重衰减系数为0.0001，稀疏性惩罚权重因子为4，稀疏性系数为0.06。其他具体参数见表2；

(5)深度神经网络的训练与测试。首先用训练集对构建的深度神经网络进行训练。通过构建的损失函数，利用梯度下降算法来调整网络的权值和缩小网络的重构误差。当训练好了网络后，再用测试集对网络进行测试。

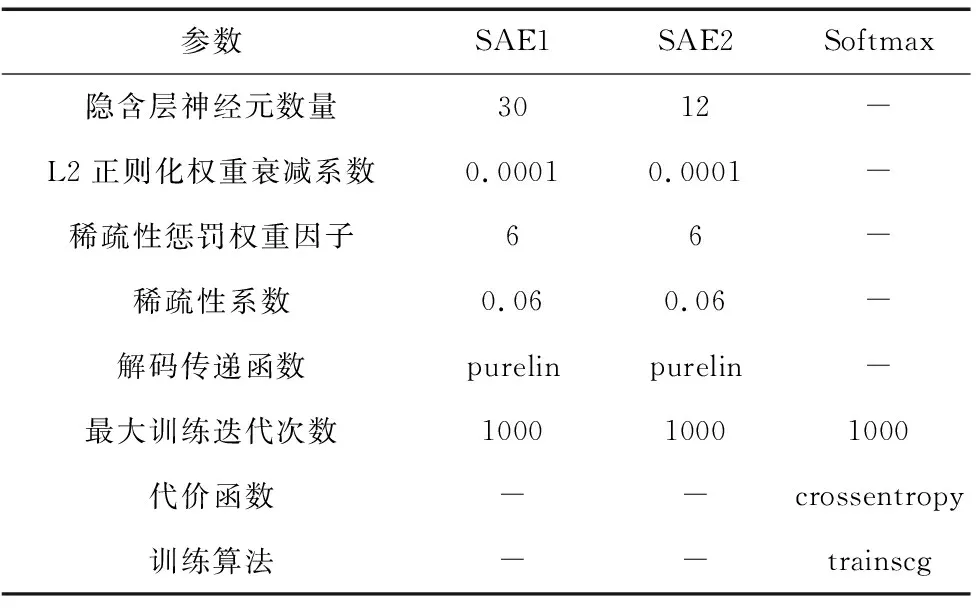
表2 DNN参数设置

3.3 实验结果

图3为提出的深度神经网络的液压泵泄漏状态的识别结果的混淆矩阵图。如图所示，混淆矩阵的横坐标与纵坐标分表代表液压泵的实际与预测状态类别，右下角方框内为综合识别精度。由图可知液压泵状态识别的综合识别精度达到了98%。对角线上的数据为每类泄漏状态中正确预测的样本数量与其在总测试集的比例，最下排为每类状态的识别精度。由图可以知道，无泄漏、弱微泄漏与严重泄漏三种状态的正确识别数量分别为193、197、198，精度分别为96.5%、98.5%与99%。由此可知提出的深度神经网络能够有效地识别液压泵的三种泄漏状态。

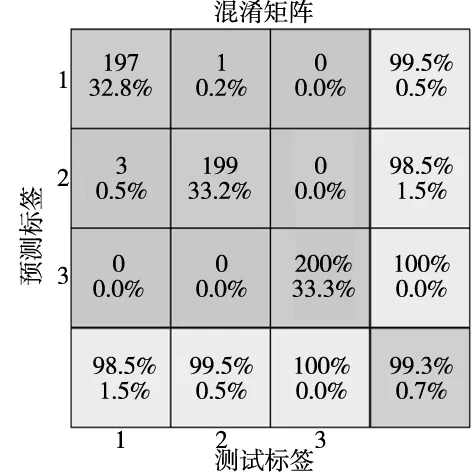
图3 DNN识别结果

3.4 SSAE高阶特征提取能力分析

本文构造的神经网络有两个稀疏自编码器构成，其中，每个稀疏自编码器隐藏层的神经元个数，即本实验中每个稀疏自编码器所用到的输出对于最终的识别精度具有一定的影响。本文基于网格搜索对两个自编码器的隐含层节点数进行了优化[16]。根据输入特征维度为7维，具体设置第一个自动编码器的隐含层节点数，从30～70，递增10个，将第二自动编码器的隐含层节点数量从4个增加到20个，每增加4个，如表2列所示。重复5次实验求平均以评估预测性能，实验结果如表3所示(表3中：*表示第二层SAE神经元个数；#表示第一层SAE神经元个数)。最后依据预测精度(ACC)设置两层神经元个数的设置数量分别为30与20。

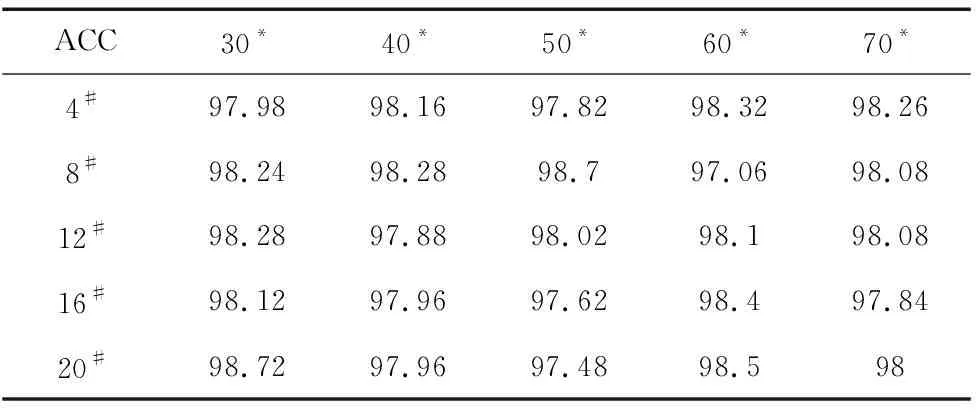
表3 DNN在不同结构下的识别精度热力图(%)

本文采取了对比实验验证提出的深度神经网络对液压泵泄漏状态识别的有效性。分别使用随机森林(RBF)与支持向量机(SVM)进行10次独立重复实验，三种模型都是用相同的训练集与测试集。图4为最终的实验分类精度结果图。由图可以看出对于液压泵泄漏状态的识别，提出的深度神经网络(DNN)具有最好的识别效果，识别精度稳定在98%左右，最高达到99.3%；RBF的识别效果有一定的波动，识别精度在96%左右；SVM的识别效果最差，识别精度在86%左右，且有一定的波动。对比实验结果表明，基于SSAE的深度神经网络相对于传统的分类模型，具有更好的特征优化能力，对液压泵泄漏状态具有更好的识别效果。

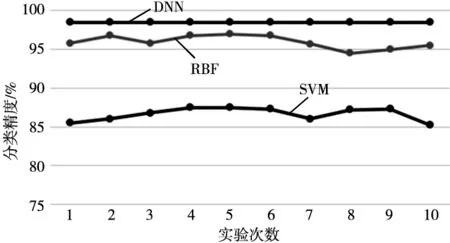
图4 实验结果对比

4 结论

本文提出了基于堆栈稀疏自编码器(SSAE)与Softmax的液压泵泄漏状态识别的深度神经网络(DNN)。通过在SSAE中引入稀疏参数的方法，在对数据的编码与解码过程中，获得更具鲁棒性的中间层数据作为高级特征使用，最后使用Softmax进行分类。实验证明，本文提出的DNN对原始低阶的小波与时域组合特征具有较好的优化性能，并最终达到较好的识别精度，最高达到99.3%，识别效果优于传统的分类器随机森林(RBF)与支持向量机(SVM)。通过SSAE对原始特征的优化能力，解决了液压信号复杂难以识别的难题，有效完成了液压泵泄漏状态的识别。未来，该DNN模型也可以用于其他复杂信号的分类识别过程中。