超声螺旋磨削制孔磨削力建模与实验研究*

林佳杰，魏 昕，杨宇辉,3，汪永超,4

(1.广东工业大学机电工程学院，广州 510006；2.广东机电职业技术学院电气技术学院，广州 510550； 3.东莞理工学院机械工程学院，广东 东莞 523808；4.东源广工大现代产业协同创新研究院，广东 河源 517500)

0 引言

硬脆材料等难加工材料具有优良的物理化学性能，对航天航空、国防军事等产业发展具有重要作用。但其加工难度较大，采用传统加工方式难以实现高效高质量加工。旋转超声加工被公认为加工硬脆材料的有效方法[1]。相比纵向超声振动加工，纵扭复合超声加工在降低切削力、提高加工质量等方面更具优势[2-3]，逐渐成为研究热点。张能等[4]探究了纵扭复合超声磨削加工工艺参数对磨削力的影响规律。Lu Y等[5]对纵扭复合超声钻削加工机理进行研究，建立了磨削力模型。

近年来，螺旋铣孔加工由于具有切削力小、易排屑、散热条件好等优势引起了学者的广泛关注。一些学者将超声振动与螺旋铣孔技术进行复合，开展了有关研究。高航等[6]开展了超声振动辅助螺旋铣削制孔加工实验，发现相比普通螺旋加工，叠加超声振动有助于降低切削力和切削温度，提高加工质量。Feng H等[7]开展了纵扭复合螺旋磨削加工盲孔、内螺纹实验，结果表明纵扭复合超声振动有助于降低切削力，提高加工质量。

磨削力是机械加工的重要过程指标，在工艺参数匹配、优化等方面具有重要的指导作用。然而，当前有关纵扭复合超声加工磨削力建模研究还较少。本文以氧化锆工程陶瓷为研究对象，在充分考虑不同超声振型及螺旋铣孔技术加工优势的基础上，采用纵扭复合超声振动螺旋磨削方式进行制孔加工，以纵向超声振动加工等磨削力建模思路[8-9]为重要参考，建立磨削力模型，并搭建磨削力测试平台开展实验进行验证，为工程应用简化工艺匹配流程、提高工艺参数优化效率等提供参考。

1 制孔工艺方式

图1为纵扭复合超声螺旋磨削制孔加工示意图，刀具轴线与孔轴线偏离一定距离，刀具在工件沿O-XY平面的进给运动和刀具沿Z轴方向进给运动的共同作用下以一定的进给速度沿着螺旋线运动；同时，对刀具施加纵扭复合超声振动、主轴转动，使刀具上的磨粒与工件相互作用，实现材料去除。结合硬脆材料的材料特性，若采用过大的螺距进行加工，容易导致磨削力过大、加工质量差及刀具磨损严重等问题，因此，本文采用小螺距方式进行加工，参与磨削的磨粒主要为端面磨粒。此时，轴向磨削力对加工过程的影响起主要作用，本文所指的磨削力均为轴向磨削力。

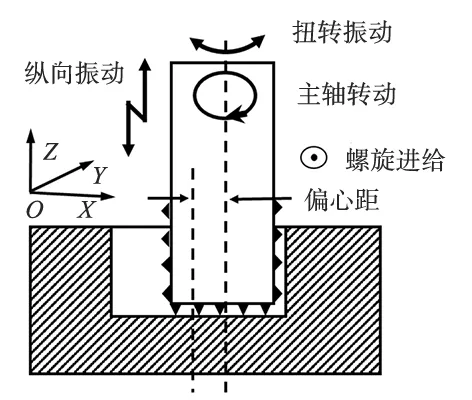
图1 加工示意图

2 磨削力建模

在纵向超声振动的作用下，刀具与工件材料周期性接触与分离，且磨粒与工件材料相互作用时切削深度不断变化。已有研究表明，工程陶瓷超声加工的材料去除方式以脆性断裂去除为主[1]。根据压痕断裂力学理论，单颗磨粒对材料的作用力Fn与切削深度δ存在以下关系[10]：

(1)

式中，ξ为磨粒压头几何因子，ξ=1.854 4；Hv为材料硬度；β为磨粒锥半角。

超声振动是压电陶瓷片在超声频率的正弦电压激励作用下产生的，其形式可按正弦振动处理。一个超声周期内，磨粒与材料相互作用的有效时间Δt为：

(2)

式中，A为纵向超声振幅；f为超声频率。

将磨粒对材料作用的轨迹波形用三角波形来替代，式(2)简化为：

Δt=δ/2Af

(3)

根据冲量定理，可知单颗磨粒在一个超声周期的平均切削力F1c为：

F1c=γ·Fn·f·Δt

(4)

式中，γ为与冲击波形有关的系数，本文的冲击波形以三角波形替代，取γ为0.5。

根据磨料浓度的有关定义，得刀具端面的磨粒总数Na为[9]：

(5)

式中，Ca为磨粒的浓度；Sa为磨粒的尺寸；Do为刀具的外径；Di为刀具的内径；C0为一无量纲常数，C0=0.03。

硬脆材料脆性断裂去除主要是侧向裂纹扩展至材料表面导致的。因此，侧向裂纹的长度、宽度及磨粒在工件表面划擦的长度综合决定一个振动周期内单颗磨粒去除的材料体积大小。结合盲孔孔底表面形貌，如图2所示，将单颗磨粒的材料去除体积抽象简化为半椭球体，如图3所示。因此，单颗磨粒在一个超声周期内的理论材料去除体积V0为：

(6)

其中，一个超声周期内单颗磨粒在工件表面划擦的距离L为：

(7)

对式(7)进行化简：

(8)

Marshall D B等[11]对侧向裂纹进行研究，得到侧向裂纹长度CL和深度CH的表达式：

(9)

(10)

式中，KIC为材料的断裂韧性；E为材料的弹性模量；v为材料的泊松比；C2为一无量纲常数，取C2=0.226。

(a)二维形貌 (b)三维形貌

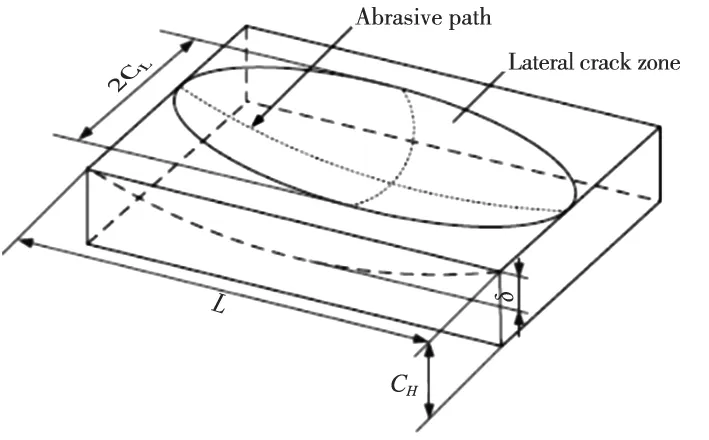
图3 单颗磨粒的材料去除体积模型[12]

理论上单颗磨粒的材料去除率MRR0为：

MRR0=fV0

(11)

因此，根据式(5)、式(11)，得到理论上所有参与磨削的磨粒材料去除率MRRN为：

MRRN=NafV0

(12)

采用螺旋磨削制孔方式加工出完整的孔或盲孔时，材料的实际去除率MRR为：

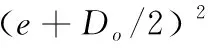
(13)

式中，vf为螺旋进给速度；e为偏心距。

此外，裂纹交织干涉等作用会导致实际材料的去除率与理论材料去除率存在一定的差异[8, 13]。因此，本文引入系数k来修正实际材料去除率与理论材料去除率之间差异：

MRR=k·MRRN

(14)

刀具所受到的磨削力看成是众多有效磨粒的叠加，假设刀具上所有参与切削的磨粒切削深度一致，根据式(4)、式(5)，得到刀具所受的磨削力Fm为：

Fm=γ·Fn·Δt·f·Na

(15)

由以上各式，单颗磨粒的切削深度的表达式可表示为：

(16)

刀具受到的磨削力Fm的表达式可表示为：

(17)

3 实验验证

3.1 实验设计

本次实验所用到的加工机床及磨削力测试系统如图4所示。超声刀柄变幅杆上存在斜槽，其作用为将部分纵向振动转化为扭转振动，实现纵扭共振。超声振幅通过设置超声输出能量百分比进行调节，超声输出能量百分比30%～70%对应的纵向超声振幅约为2.5～6 μm，谐振频率约为21.7 kHz，纵扭比约为3:1，相位差约为60°。采用Kistler9129AA动态压电式测力系统实时采集加工过程的磨削力。为了减少加工过程切削液喷射产生冲击力而造成的测量误差，加工前先打开切削液，然后打开测力仪采集切削液的冲击力数据，待切削液稳定喷射后，对测力仪进行调零设置，从而减少切削液冲击力的影响，保证所采集磨削力数据的准确性。所用工件材料氧化锆陶瓷的力学性能见表1。刀具为外径4 mm，内径2 mm，磨粒粒度为180目的中空电镀金刚石刀具。通过对磨粒形貌的观察，假设磨粒为正四棱锥状，锥顶角为90°。

图4 磨削力测试系统

式(17)存在一个有关实际去除率与理论材料去除率之间关系的修正系数k，该系数可通过实验数据拟合得到。裂纹交织干涉作用、重复切削等[8]会影响材料的去除率。充分考虑超声振动对裂纹系统的影响并结合加工实际，认为修正系数k主要与螺距ap、主轴转速n、螺旋进给速度vf、超声振幅A等有关。因此，本文开展2组单因素实验，一组是为了获取修正系数k与工艺参数的关系，实验参数如表2所示；另一组是为了验证所建立的磨削力模型的有效性，实验参数如表3所示。两组实验的偏心距均为1mm，且其他条件保持一致。实验后对所采集的磨削力信号进行平滑化处理，选取稳定磨削加工的信号段，借助Dynowave软件计算平滑后磨削力信号的平均值。

表1 氧化锆工程陶瓷的力学性能

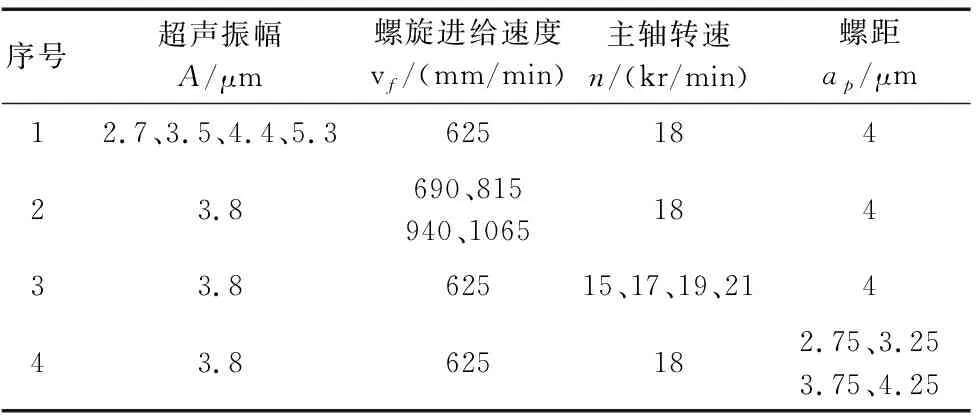
表2 修正系数k获取实验参数

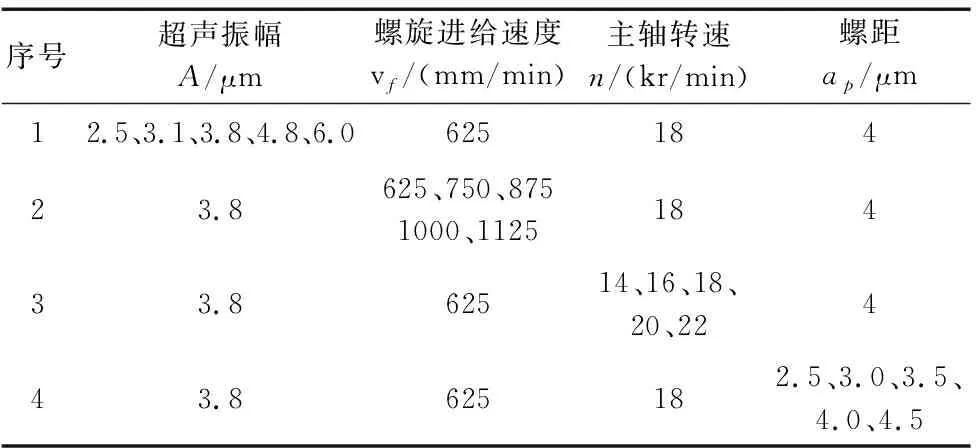
表3 模型验证实验工艺参数

3.2 修正系数k计算结果

假设修正系数k与工艺参数存在以下关系：

k=a0na1apa2vfa3Aa4

(18)

根据表2进行实验后，结合磨削力的建立过程，将平均磨削力代入反求算出k值，并利用最小二乘估算法对系数k进行拟合，得到修正系数k与工艺参数的关系为：

k=2.896×10-9·n1.286·ap-0.723·vf-0.5539·A0.683

(19)

3.3 实验结果与分析

图5～图8为磨削力模型预测结果与表3实验结果的对比图。从图5～图8可以看到模型预测结果与实验结果的变化趋势一致且数值均较为相近，验证了所建模型的正确性，也表明了建立模型所提出的假设合理。

此外，该结果还反映工艺参数对磨削力的影响规律。如图5所示，磨削力随超声振幅增大逐渐减小，这是由于超声振幅增大，由式(3)可知，有效切削时间减少，因而使磨削力降低。超声振幅为3.1 μm～6.0 μm时，模型的预测精度较高；而超声振幅为2.5 μm时，预测值与实验值有一定差异，且实验值大于预测值，这是因为超声振幅较小，无法充分发挥超声振动的加工优势，加工过程趋向于普通磨削加工，使实际加工条件与模型建立假设条件存在差异，进而导致预测精度降低。由图6可知，磨削力随螺距的增大逐渐增大，这是因为螺距增大实质上是增大了磨粒的切削深度，单位时间内材料去除量也相应增大，从而使磨削力增大。从图7可知，磨削力随螺旋进给速度增大而增大，这是由于螺旋进给速度增大使得材料去除率提高，从而增大了磨削力。由图8可知，磨削力随主轴转速的增大而减小，这是由于主轴转速提高，使单位时间内参与磨削的磨粒增多，使得单颗磨粒对材料的切除量减少；同时也有利于形成更小的切屑及时排出加工区域，减少刀具磨损等，从而有效地降低切削力。

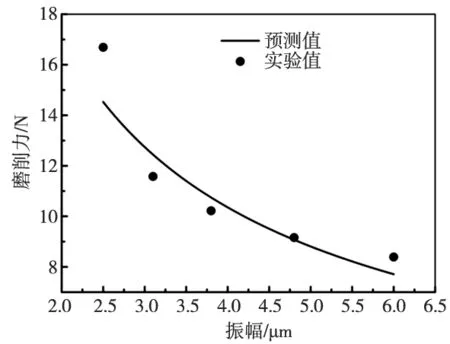
图5 超声振幅对磨削力的影响

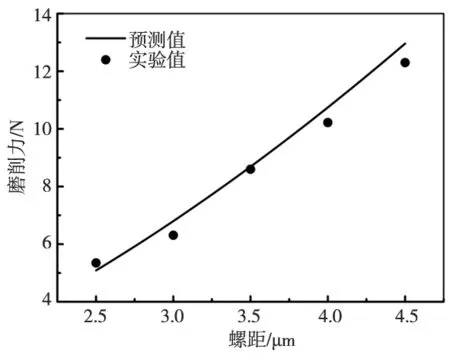
图6 螺距对磨削力的影响

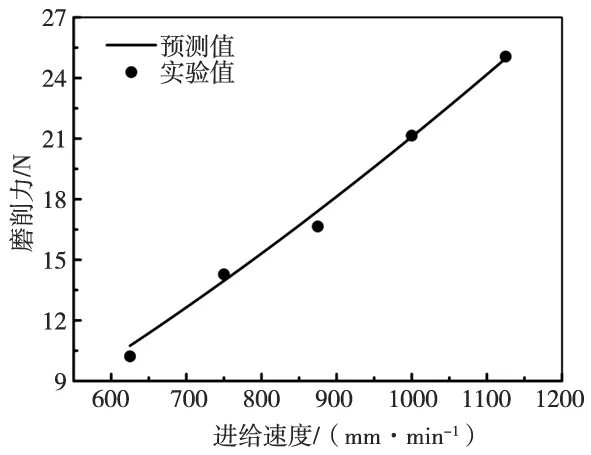
图7 螺旋进给速度对磨削力的影响

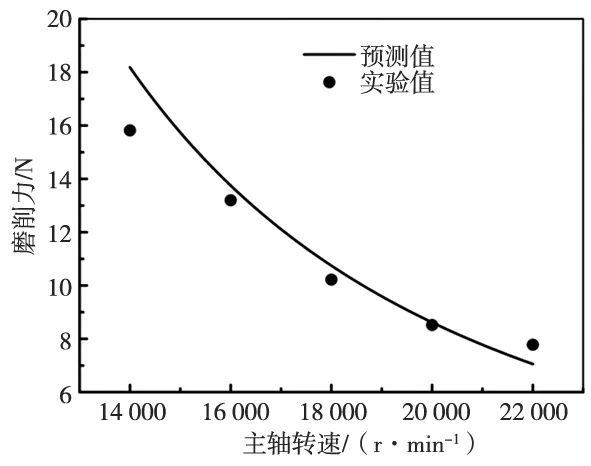
图8 主轴转速对磨削力的影响

4 结论

(1)基于压痕断裂力学理论，建立了纵扭复合超声螺旋磨削制孔磨削力预测模型，并通过氧化锆陶瓷磨削制孔加工实验对模型进行了验证，结果表明模型预测结果与实验结果具有相同的变化趋势，且数值相近，验证了模型的正确性及模型相关假设的合理性。

(2)为修正材料理论去除率和实际去除率的误差，引入修正系数进行修正。结合加工实际，假设修正系数与超声振幅、主轴转速、螺旋进给速度及螺距有关，通过对实验结果进行拟合，得到了修正系数与工艺参数的经验公式。

(3)磨削力随着超声振幅、主轴转速的增大而减小；随着螺旋进给速度和螺距的增大而增大。