高比表面积周期性多孔结构拓扑优化*
杜义贤,罗明亮,付君健,2,田启华,周祥曼,孙鹏飞
(1.三峡大学机械与动力学院,湖北 宜昌 443002;2.水电机械设备设计与维护湖北省重点实验室,湖北 宜昌 443002)
0 引言
周期性多孔结构是功构一体化的优良载体,具有高比表面积、高比刚度、高比强度、隔热、隔音等特性[1-2]。在电化学和生物工程领域,周期性多孔结构比表面积大小对结构性能具有重要影响。例如,在锂电池领域,电极中含有多孔式的集流体结构,其表面包覆有活性材料,集流体结构比表面积大小决定活性材料的分布[3],对锂离子扩散系数、电子导电率、锂离子存储空间有重要影响。在化学工程领域,为了增大催化剂与反应物的接触面积,多孔催化剂载体结构需要有较高的比表面积[4]。在生物工程领域,较高比表面积和合适孔径大小的骨支架有利于细胞在其中生长[5]。因此,比表面积大小是周期性多孔结构重要的工程设计参数。拓扑优化通过调控结构的参数,将结构参数与性能联系起来[6],从而获得高比表面积的拓扑构型。
拓扑优化是周期性多孔结构的重要设计方法[7]。通过施加周期性边界条件约束,拓扑优化可在设计域内寻找满足目标函数和约束条件的最优材料分布[8]。提高周期性多孔结构比表面积的拓扑优化设计方法可分为两类:一类是基于均匀化[9-10]的设计方法;另一类是基于宏观周期性约束的设计方法[11]。例如,采用均匀化法计算复合材料的性能参数,实现单胞内材料的重新分配[12],有效提高了周期性多孔结构的比表面积;在单一体积约束下,基于能量均匀化法,对结构等效属性评价[13],可得到具有高比表面积的周期性多孔结构。但是,采用均匀化方法进行高比表面积周期性多孔结构设计,其尺度分离假设会带来微结构单胞间材料不连通的问题,不具备制造性。此外,将宏观设计域分解为若干子区域,利用子结构凝聚构建超单元计算模型减少有限元计算量[14-15],组装子结构可得到高比面积周期性多孔结构。对宏观周期性多孔结构的最大尺寸进行限制,可进一步提高其比表面积。然而,基于宏观周期性约束的高比表面积多孔结构设计方法存在大量约束问题,不便于计算。
本文提出了一种高比表面积周期性多孔结构拓扑优化方法,引入局部体积约束,使设计域内材料进一步分散,显著提高了结构的比表面积。通过p-norm函数将多体积约束凝聚为单一体积约束,解决了宏观周期性约束产生的大量约束问题,提高了拓扑优化的求解效率。数值算例验证了本文方法的有效性。
1 周期性多孔结构的定义
本文采用宏观周期性约束方法,将整体设计域划分为若干个相同大小的子区域,如图1所示。所有子区域中相同位置单元的相对密度保持一致,从而使各子区域具有相同的拓扑形式,以保证结构的周期性[11]。各单元密度关系的数学表达式为:
x1,j=x2,j=…=xm,j
xi,j∈[0,1](i=1,2,…,m;j=1,2,…,n)
(1)
式中,xi,j为设计变量,表示第i个子区域内第j个单元的密度;m为总设计域划分的子区域个数,n为子区域内单元数量。
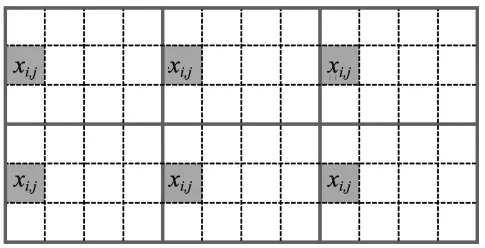
图1 二维周期性结构设计域
2 局部体积约束
假定拓扑优化设计域内材料分布由逻辑值ρe表示,ρe=1或0代表实体单元或孔洞单元。为了限制设计域内材料积累形成大的实体区域,引入局部体积约束使设计域内材料进一步分散。
(2)
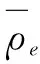
(3)
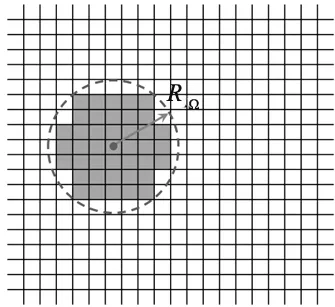
图2 局部体积约束
(4)
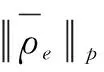
(5)
式(5)可重新写为:
(6)
式中,N是整体设计域内单元总数量。p越大,每个单元的约束就越强,同时也增加了问题的非线性。
引入一个数值从0~1连续变化的单元密度xe作为拓扑优化设计变量,为去除中间密度单元产生的棋盘格现象[17],通过局部滤波器计算相邻单元的加权平均值对xe过滤:
(7)
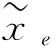
(8)
式中,re为敏度过滤半径,其数值小于图2中集合Ne的半径RΩ;oi和oe为单元中心;式(7)中权重因子Wi,e大小和oi、oe两单元中心距离有关:
(9)
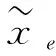
(10)
式中,参数β控制阈值函数斜率,如图3所示。当β越大时,函数值越接近0或1。如果直接应用一个较大β值,会导致高度非线性解;因此,本文从β=1开始迭代,经过一定迭代次数后,将其数值翻倍,这个过程称为参数扩展,可提高优化求解的收敛性[18]。
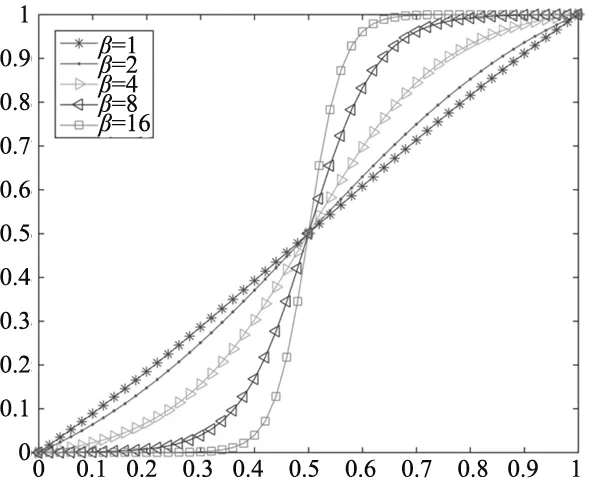
图3 不同参数β控制的Heaviside函数
3 拓扑优化数学模型
基于改进固体各向同性(Modified Solid Isotropic Material with Penalization, modified SIMP)的变密度法材料插值模型[19],建立单元杨氏模量Ee数学表达式:
(11)
式中,E0为实体单元刚度值;Emin为一非常小的数值,代表孔洞单元刚度值,以防止整体刚度矩阵产生奇异值;γ为单元密度的惩罚因子,对拓扑优化中具有中间密度的单元进行惩罚,使其收敛于指定的密度上下界,从而抑制灰度单元。任意单元刚度矩阵Ke为:
Ke=Ee(ρe)k0
(12)
式中,k0为实体单元刚度矩阵。
引入局部体积约束对设计域内的材料分布进行限制,基于改进SIMP插值模型,以单元相对密度xe为设计变量,构造多孔结构周期性约束条件,以结构刚度最大化为优化目标,建立拓扑优化数学模型:
find:xe= {x1,j,x2,j,x3,j,…,xi,j}
(i= 1,2,…,m;j= 1,2,…,n)
(13)
式中,c、K、U、F分别为整体柔度、刚度矩阵、位移向量、载荷向量;g(x)为局部体积约束方程,控制结构比表面积大小。
4 敏度分析
基于式(13)的拓扑优化数学模型,以单元相对密度xe为设计变量,采用有限元移动渐近线方法[20](Method of Moving Asymptotes, MMA)来更新设计变量,需要分别计算目标函数柔度c和局部体积约束方程g(x)对设计变量xe的一阶导数,用链式法则计算如下:
(14)
(15)
由式(11)、式(13)得:
(16)
式(14)、式(15)中其他部分导数为:
(17)
(18)
(19)
(20)
为保证式(13)中每个子区域第j个单元的密度相等,需要对敏度平均:
(21)
5 数值算例
本文采用悬臂梁和Michell梁拓扑优化算例,分别计算和对比有、无局部体积约束的周期性多孔结构表面积,验证本文提高结构比表面积方法的有效性。在三维空间中,比表面积是指多孔结构单位质量所具有的孔洞总面积[21],可定义为:面积/体积;在二维平面中,比表面积是指多孔结构单位面积所具有的孔洞总周长,可定义为:长度/面积。材料弹性模量E=1,泊松比u=0.3,单元大小默认为1(所有单位均为无量纲值),以结构刚度最大为目标建立优化模型,采用MMA算法进行求解。
5.1 悬臂梁
图4所示为悬臂梁结构,其设计域竖直方向和水平方向的长度分别为:H=100,L=200。左侧边界固定,右侧边界中间节点加载一竖直向下的集中载荷F。有限元单元为四节点矩形单元,采用200×100网格离散设计域,划分为4×2大小的子区域,总体体积分数为0.45。
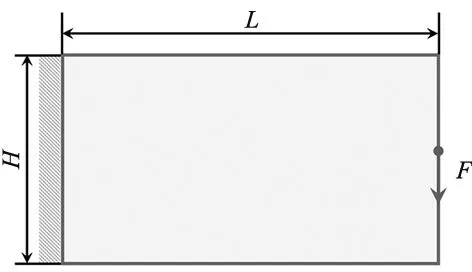
图4 悬臂梁结构的设计域示意图
取局部体积分数上限α=0.6,有、无局部体积约束的周期性多孔结构对比如图5所示,其迭代过程如图6所示。
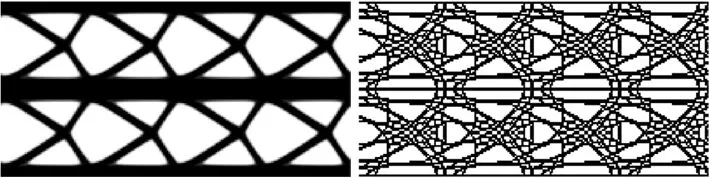
(a) 无局部体积约束 (b) 有局部体积约束图5 悬臂梁拓扑优化结构对比图
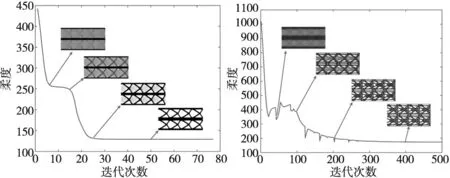
(a) 无局部体积约束 (b) 有局部体积约束图6 悬臂梁拓扑优化迭代曲线
由图5可以得出,无局部体积约束的结构杆件较为粗壮;有局部体积约束的结构最大尺寸减小,拓扑优化构型细节特征增加,孔径变小,孔洞数量增多。图6为悬臂梁拓扑优化迭代曲线,图6a为无局部体积约束的迭代曲线,整个优化过程收敛平稳,目标函数柔度c最终收敛于129;图6b给出了局部体积分数上限α=0.6、p-norm函数控制参数p为16时的迭代曲线,Heaviside函数控制参数β每迭代40次数值翻倍,因而目标函数每隔40步会出现短暂的波动,目标函数柔度c最终收敛于173。因此,对比有、无局部体积约束的周期性结构拓扑构型可以得出,有局部体积约束的结构细杆特征增加,结构柔度变大,实现了最大尺寸约束,具有更高的比表面积。
因周期性多孔结构每个单胞完全一样,为减少计算量,测量、对比其单胞的表面积即可。拓扑优化原始构型存在孔洞边缘“模糊”、表面不光滑的问题,往往不能直接精确绘制其孔洞边缘,从而无法准确测量比表面积。为解决该问题,采用水平集方法(Level Set Method)[22-23]对周期性多孔结构的原始单胞进行后处理。以单胞拓扑构型图的像素为单位测量孔洞总周长,即为表面积,结果见表1。在悬臂梁算例中,具有局部体积约束的拓扑构型比表面积(比表面积与表面积成正比)提高了约300%,验证了本文方法的有效性。
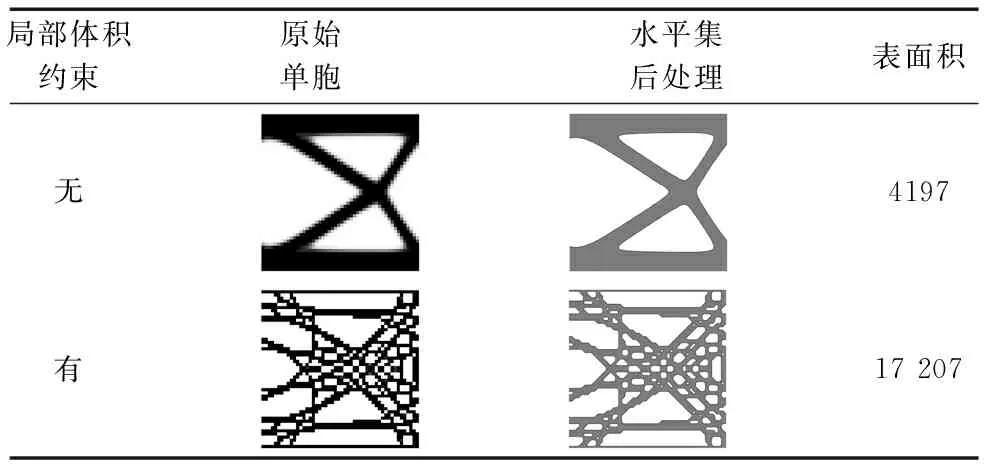
表1 悬臂梁单胞拓扑构型对比
5.2 Michell梁
图7所示为Michell梁结构,其设计域竖直方向和水平方向的长度分别为:H=100,L=200。左侧边界底部为简支支撑,右侧边界底部为固定支撑,底部中间加载一竖直向下的集中载荷F。有限元单元为四节点矩形单元,采用200×100网格离散设计域,划分为4×2大小的子区域,总体体积分数为0.45。
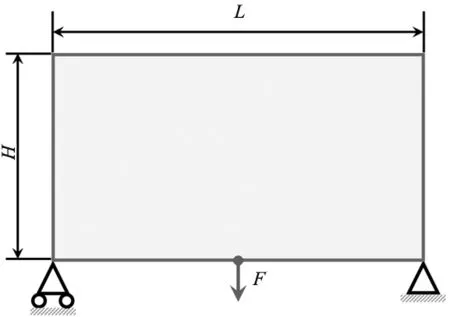
图7 Michell梁结构的设计域示意图
取局部材料体积分数上限α=0.6,有、无局部体积约束的周期性多孔结构对比如图8所示,其迭代过程如图9所示。
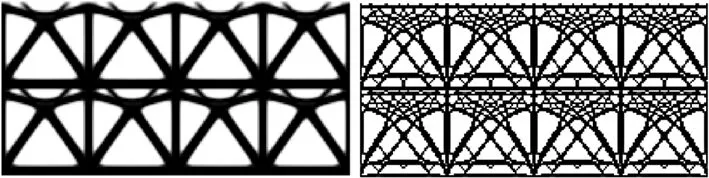
(a) 无局部体积约束 (b) 有局部体积约束图8 Michell梁拓扑优化结构对比图
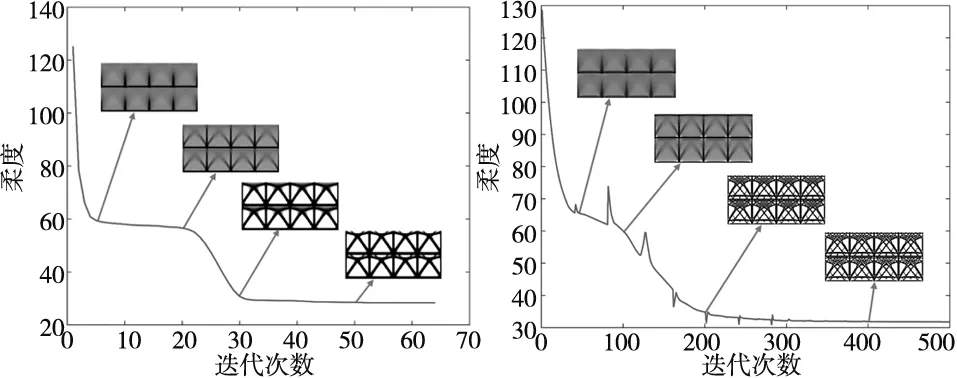
(a) 无局部体积约束 (b) 有局部体积约束图9 Michell梁拓扑优化迭代曲线
由图8可以得出,在Michell梁算例中,有局部体积约束的周期性拓扑构型具有更多的细节特征,孔洞数量增多。图9 Michell梁拓扑优化迭代曲线中,无局部体积约束的周期性结构柔度c最终收敛于28;有局部体积约束的周期性结构柔度c最终收敛于32。因此,有局部体积约束的结构细杆特征增加,结构柔度变大,实现了最大尺寸约束,具有更高的比表面积。单胞拓扑构型及表面积大小具体见表2。在Michell梁算例中,本文提出的局部体积约束方法将拓扑构型的比表面积提高了约200%,验证了该方法的有效性。
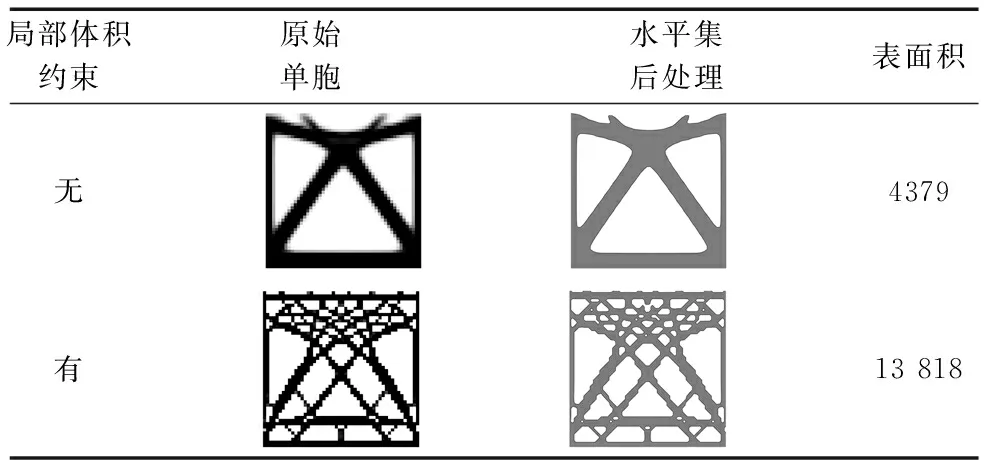
表2 Michell梁单胞拓扑构型对比
6 结论
本文提出了一种高比表面积周期性多孔结构拓扑优化方法,通过引入局部体积约束,使设计域内材料进一步分散,对周期性多孔结构的最大尺寸实现了有效控制,显著提高了结构的比表面积。通过p-norm函数将多体积约束凝聚为单一体积约束,解决了局部体积约束产生的大量约束问题,提高了拓扑优化的求解效率。使用水平集方法对周期性结构单胞进行后处理,得到光滑边界的拓扑构型,从而在数据分析软件中精确测量了结构的表面积。拓扑优化经典二维数值算例验证了本文方法的有效性。

