新型非对称打磨并联机构运动学分析与仿真*

赵新华,戴腾达,刘 凉,冯建峰,张青云

(天津理工大学 a.天津市先进机电系统设计与智能控制重点实验室;b.机电工程国家级实验教学示范中心，天津 300384)

0 引言

相对于传统数控机床，并联机床有刚度大、结构紧凑、响应速度快等优点，所以广泛的应用于高精度、复杂零部件的打磨加工[1]。少自由度尤其是三自由度并联机构，由于制造和控制成本低，所以其在并联机床的应用逐渐成为学术界和工业界的研究热点。文献[2]中提出一种三自由度并联机床，对机床运动学和动力学性能进行分析，但它含有球铰，导致关节精度制造难度加大和成本提高；针对涡轮叶片部分难加工的问题，提出一种可以对其进行高精度加工的并联机床机构方案[3]，但其组成支链多且结构复杂，驱动关节累积误差大。1983年，Hunt首次成功提出了三自由度的3-RPS并联机构，该机构被广泛用于并联机床、光电跟踪等领域[4]。黄真、李秦川等提出了螺旋综合理论和位移子群等理论，使并联机构理论体系更加完善[5-6]。文献[7]中借助螺旋理论，通过对力和力矩的效率研究，对机构的运动学性能进行分析。文献[8]针对三自由度并联机构提出一种基于轮廓误差的同步滑模控制方案，实现了精确的运动跟踪。赵永生、杨彦东等提出了3PSU&S和3UPS&S并联机构，定义了机构功率传递系数，以此均值作为机构运动学的性能指标[9-10]。文献[11-13]对不同三自由度的并联机构采用矢量闭环等方法完成了运动学的建模。

为此，文中提出一种新型的两移一转三自由度的非对称并联机构2RRRU-PRRU，它不含球铰且两RRRU分支呈对称分布，不仅能提高机构响应速度、减少驱动关节累计误差，还能保证系统运动精度。同时基于矢量闭环矢量法建立系统各构件之间的运动学关系，并通过运动学分析得到了末端轨迹与执行构件的位置、速度变化规律，再运用ADAMS软件建立系统的虚拟样机仿真模型，最后通过理论数值模型和虚拟样机仿真模型的交叉验证，印证了模型建立的正确性。

1 机构构型分析

1.1 机构描述和坐标系建立

机构的初始位型如图1所示，由支架、动平台、静平台、移动副导轨、两条RRRU分支和一条PRRU分支构成。静平台、移动副导轨均固接于支架，RRRU两分支呈对称分布。RRRU分支中，虎克铰(U)与动平台相连接，转动副(R)与静平台相连接。PRRU分支中，移动副(P)与移动副导轨相连接，虎克铰(U)与动平台相连接。

图1 2RRRU-PRRU虚拟样机模型图

该机构的位置分析模型如图2所示。在静平台建立静坐标系O-XYZ，在动平台创建动坐标系p-uvw。RRRU分支中的转动副和虎克铰中心点依次记为Ai1、Ai2、Ai3和Ai4(i=1,2)。 PRRU分支中移动副中心A6与OXY平面的交点记为A5，第二个转动副中心记为A7。静坐标系O-XYZ中O为A11A21的中点，X轴由点O指向A21，Y轴由O点指向A5，Z轴满足右手定则。动坐标系p-uvw的建立方法与之相同。令OA21=R，PA24=r，OA5=e，A11A12=l1，A12A13=l2，A13A14=l3，A6A7=l4，PA7=l5。

图2 2RRRU-PRRU并联机构简图

1.2 自由度分析

修正的Kutzbach-Grubler公式能准确的分析包含局部自由度甚至过约束的并联机构的自由度。因此，采用此方法来分析计算该机构的自由度，其公式表达式为：

(1)

式中，M为机构的自由度；d为机构的阶数,d=6-λ；λ为公共约束数目；n为构件数目；g为运动副的数目；fi为第i个运动副的自由度；v为冗余约束数目；ζ为局部自由度数目。

在该机构中，λ=0；由图2可知，总构件数n=11；f=1的运动副数量为9，f=2的运动副数量为3，所以g=12；由于该机构不存在冗余约束和局部自由度，所以v=0，ζ=0。将其代入式(1)，则有：

M=6×(11-12-1)+15=3

以上分析可得该机构具有3个自由度，根据图1构型和螺旋理论可知，机构前两个支链的运动螺旋为：

(2)

式中 ，s=sin，c=cos，i=1, 2；u1,v1,t1,u2,v2,t2,u3,t3均为实数，与支链各运动轴线的空间位置有关。

第3个支链的运动螺旋为：

(3)

式中，u4,t4,u5,a1,b1,u6,t7均为实数，与第3支链各运动轴线的空间位置有关。

这3个支链的约束反螺旋为：

(4)

式中，前两个约束为约束力偶，方向分别沿第一支链和第二支链杆件Ai2Ai3(i=1,2)的轴线；第3个约束为约束力线矢，方向沿X轴向。因此，该机构3个自由度分别是绕着Y轴的转动以及Y轴和Z轴的平动。它可用于对半圆形筒状工件内壁的打磨加工，即在动平台末端安装打磨装置与夹具，将工件固定在加工平台上，并联机构的动平台可沿筒状工件的轴线方向对工件内壁表面进行打磨，如图1所示。

2 机构位置反解

该机构具有两移一转3个自由度。因此可用(θ,Py,Pz)3个参数来描述动平台与静平台的位姿关系。则动坐标系P-uvw变换到定坐标系O-XYZ的变换矩阵为：

(5)

两条RRRU分支中定义的关节变量，如图3所示。其中，θi1(i=1,2)为驱动角度，θi2和θi3(i=1, 2)为第二和第三转动副的转动角度。

图3 RRRU分支在不同平面中的关节变量(i=1, 2)

根据几何法，在XOZ平面内该分支的矢量闭环方程为：

OAi1+Ai1Ai2+Ai2Ai3+Ai3Ai4=OP+PAi4

(6)

将式(6)右端展开为:

(7)

将式(6)左端展开为:

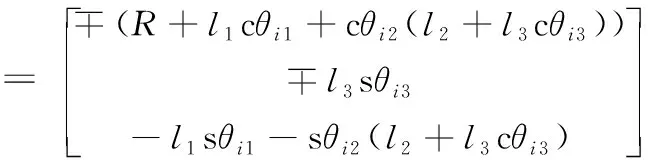
(8)

联立式(7)和式(8)可得:

(9)

根据式(9)即可得驱动角θi1：

(10)

(11)

式中，K5=K1+K3-K4；

K6=2K2；

K7=K1-K3-K4；

K2=2l1(Pz±rsθ)；

K3=2l1(rcθ-R)；

K4=(l2+l3cθi3)。

从式(11)可以看出，θi3只与动平台的位置有关，它有两种可能的取值；由于K4与θi3有关，所以K4有两种取值，由式(10)可知，驱动角θi1则有四种可能的取值。

PRRU分支如图4所示，其中d为驱动位移，α为支链与静平台的夹角。从图中可知动平台位置确定时该分支有两种位置构型，在这里我们选择A6A7为虚线时的构型，此时Pz<0。

图4 PRRU分支所组成平面

在YOZ平面内该分支的矢量闭环方程为：

OP=OA5+A5A6+A6A7+A7P

(12)

将式(12)展成Y和Z方向的两个分量式:

(13)

消去α可得:

(14)

综上所述，驱动角θ11和θ21均有4组反解；PRRU分支中驱动输入d实际上有两组反解。因此，2RRRU-PRRU并联机构的位置反解共有32组。

3 机构速度反解

3.1 RRRU分支速度反解

首先，求解RRRU分支的速度反解，对式(6)两边求导可得:

VP=Oωi1×ai+Oωi2×bi+Oωi3×ci+Oωi4×fi

(15)

式中,Vp为动平台点P的线速度；ωij为第i条支链第j个转动副的角速度；ai为向量Ai1Ai2；bi为向量Ai2Ai3；ci为向量Ai3Ai4；fi为向量Ai4P；

在式(15)两边对向量ci作数量积，可得：

VP·ci=(0ω1i×ai)·ci+(0ω2i×bi)·ci+(0ω4i×fi)·ci

(16)

将上面数值带入式(16)则有：

(17)

将式(17)写成雅克比矩阵形式：

(18)

其中，

(19)

(20)

化简整理可得：

(21)

(22)

其中两分支的φ值分别取180°和0°，所以速度反解:

(23)

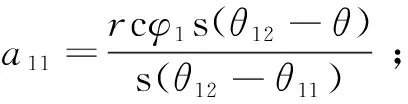
3.2 PRRU分支速度反解

在PRRU分支中，对式(14)两端求导即可建立该分支的速度方程:

(24)

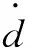
化简整理可得:

T=[Pz-d]

(25)

(26)

即:

(27)

综上各支链的速度反解公式，该机构的速度雅可比矩阵为:

(28)

4 机构运动学仿真

为了验证运动学模型的正确性和研究机构运动规律，基于同等条件，将理论模型通过MATLAB编程求解，并与仿真软件ADAMS的运动学仿真结果进行对比分析。设虚拟样机中打磨装置的工作面到动坐标系原点的距离为H，如图5所示，则末端执行器工作点在动坐标系下的坐标为E=(0 0 -H)T。而在静坐标系下的坐标为:

(29)

即:

(30)

图5 打磨装置结构图

仿真运动轨迹设为螺旋线，起点位置为(-0.1, -0.4, -1) m，角速度为2 rad/s，导程为0.05 m，方向为沿Y轴正方向，范围为[-0.4,0.4] m，运行时间为8 s，具体运动轨迹方程为：

(31)

式中,ω为角速度；Ph为导程；t为运行时间。

其余仿真参数如表1和表2所示。

表1 RRRU支链仿真参数

表2 PRRU支链和刀具仿真参数

4.1 基于MATLAB的数值仿真模型

基于上述运动学关系，通过MATLAB软件进行编程求解可得驱动关节位移随时间的变化曲线，如图6和图7所示。其中，图6为并联机构RRRU两分支驱动角随时间变化的曲线，而图7为PRRU分支驱动位移随时间变化的曲线。

图6 RRRU支链驱动关节角位移 图7 PRRU支链驱动关节位移

由图6和图7可知：驱动角和驱动位移的变化过程平滑且变化规律呈对称和类似正弦函数趋势，整个过程无突变现象。但两个RRRU分支驱动角存在相位差和峰值差，这是因为机构仿真运动轨迹起点为(-0.1, -0.4, -1) m，即初始位置下驱动角第二支链大于第一支链，且变化规律上第二支链滞后于第一支链。同时在给定驱动参数的情况下，RRRU分支两个驱动角的变化区间约为[4.5°, 41.3°]，幅度大约为36.8°；PRRU分支驱动位移区间约为[-1.46,-1.94] m，幅度约为0.48 m。

RRRU两分支驱动角速度和PRRU分支移动速度随时间变化的曲线如图8和图9所示。

图8 RRRU支链驱动关节角速度 图9 PRRU支链驱动关节速度

由图8和图9可知：在整个变化过程中，驱动角速度和移动副速度在一定范围内变化，运动过程平稳，不存在突变情况，整体变化呈类似正弦函数的趋势。RRRU分支的驱动角的速度变化区间为[-31.3,31.2] deg/s，幅度约为62.5 deg/s； PRRU分支驱动速度区间约为[-0.29, 0.18] m/s，幅度约为0.47 m/s。

通过数值仿真模型的结果可知，驱动关节位移和速度的仿真结果均呈现出类似正弦函数的变化趋势，且由于仿真轨迹在Y轴上范围为[-0.4,0.4] m，所以RRRU分支驱动角位移的变化呈对称趋势，而PRRU分支驱动关节位移呈现出周期性下降趋势。因为位移和速度的数值仿真结果与理论求解的运动方程相对应，且两者之间存在着明显的导数关系，从而验证了运动学模型的正确性。

4.2 基于ADAMS软件的虚拟样机仿真模型

利用Unigraphics NX 10.0和ADAMS软件在同等参数条件下建立该机构的虚拟样机模型，并对其进行运动学分析。虚拟样机仿真模型为图1去除支架和工件的三维模型，之后将其导入ADAMS中，并将MATLAB数值仿真结果作为其驱动函数。利用ADAMS中的Controls等模块可得到该机构各驱动关节的位移、速度仿真曲线和末端工作点的仿真运动轨迹如图10～图14所示。

通过ADAMS和MATLAB驱动关节角位移变化曲线对比可知： 两类模型的RRRU支链和PRRU支链的驱动关节位移均呈对称和类似正弦函数变化趋势，且过程平滑，但由于两者初始零位不同，导致位移曲线存在位差。根据图12、图13与图8、图9的对比结果可知，各支链驱动关节速度变化与MATLAB一致。

图10 RRRU支链驱动关节角位移

图11 PRRU支链驱动关节位移

图12 RRRU支链驱动关节角速度

图13 PRRU支链驱动关节速度

从ADAMS仿真结果上看，虚拟样机仿真结果与MATLAB数值仿真结果一致，所以进一步对比验证了运动学模型的正确性。同时由图14可知：虚拟样机仿真轨迹为沿着Y轴运动的螺旋线，证明该机构具有沿Y和Z轴两个平移自由度及绕Y轴的旋转自由度，验证了机构的可行性。

图14 末端执行器的螺旋线运动轨迹

5 结论

(1)运用螺旋理论对该机构自由度进行分析，得出其具有两移一转三个自由度；基于闭环矢量法建立该机构的运动学模型，分析了末端轨迹与执行机构之间的位置和速度关系。

(2)利用MATLAB软件建立理论数值仿真模型。结果表明：由于运动支链关节的差异导致角度变化也不尽相同。其中，RRRU分支驱动关节角位移变化区间约为[4.5°, 41.3°]，变化规律呈对称分布；PRRU分支驱动关节移动副位移变化区间约为[-1.46, -1.94] m，变化规律均呈类似正弦函数的下降趋势，并且两分支驱动角变化规律存在相位差和峰值差异。

(3)根据驱动关节的速度规律可知：三条分支的驱动关节速度与时间的变化过程较平滑、无突变现象，其变化规律均呈类似正弦函数趋势，且位移与速度之间有明显的导数关系，验证了运动学模型的正确性。

(4)利用Unigraphics NX 10.0和ADAMS软件建立的虚拟样机仿真模型与理论数值仿真模型的逆运动学分析结果一致，从而相互印证了模型的正确性，为后续的动力学研究及控制研究奠定了基础。