实变函数课题式教学研究

曹广福

实变函数课题式教学研究

曹广福

（华南农业大学 数学与信息学院，广东 广州 510642）

课题式教学可以有效地解决课程的完整性与课时数不足之间的矛盾，实变函数课题式教学首先需要引导学生了解实变函数的产生与发展以及面临的重要问题．理清实变函数的主要脉络、把握实变函数的主要思想方法．通过测度论课题式教学案例说明如何实施课题式教学．强调不仅要学会发现问题，同时还能对问题的重要性与科学价值进行甄别，在分析问题的过程中学会思辨，掌握科学的思维方法．

勒贝格测度；可测函数；勒贝格积分；课题式教学

1 问题提出

随着大学课程改革，很多课程的课时数大大压缩，对学生自主学习的要求大大提高．实变函数作为大学数学专业学生普遍感觉难学的专业基础课，其课时不仅大大压缩，而且各学校的课时设置有着很大差别．如何在不同的课时内不降低课程要求的前提下完成该课程的完整教学内容是个有难度的问题，课题式教学是解决这一难题的合适方法，通过实变函数课程的教学说明如何开展课题式教学．所谓课题式的本质是课堂教学从宏观上把握学科产生与发展的来龙去脉，围绕着促使理论产生的一系列问题展开，通过问题的发现、分析与解决从而完成数学的再创造．课题式教学不仅回归了教育的本质，而且极大增强了课堂的弹性，既适用于多课时也适用于少课时．

如文[1]所述，在课程内容开始之前，学生对课程应该有一个宏观的了解，这就是文[1]的架构图中所说的总览．具体地说，学生应该清楚为什么要学这门课程？它为什么产生？为了解决什么问题？解决问题的关键是什么？问题的难点在哪里？无论教学课时多或少，这个过程是必不可少的，因为它涉及到对课程整体结构的了解．如果教学时数宽裕则需要精雕细琢，通过对问题的深入剖析详细演绎出重要的思想方法，并得出相关的概念与定理．

2 实变函数教学的整体设计

从教法层面看，教师需要处理好几个重要问题．

（1）理清实变函数的主要脉络．思想是通过知识呈现的，要完整地展现某种思想，知识的主线少不了．例如，判断集合可测的分割性条件；可测集与波雷尔集之间的关系；处理一般函数的最基本定理：叶果洛夫定理；架设连续函数与可测函数之间桥梁的鲁津定理；勒贝格积分的精髓：控制收敛定理．这些知识内容构成了实变函数的主线，也是实变函数的精髓．

（2）把握实变函数的主要思想方法．如何通过知识的脉络在有限的课时内尽展实变函数的思想方法？这是有难度的事情．首先需要把它的思想方法梳理清楚！那么，实变函数的基本思想方法是什么？从处理问题的角度看，它有3个核心思想：①以特征函数作为构成可测函数的基本单元，通过它可以构造所有的可测函数；②通过“微创”手术，将较弱的收敛性转换成一致收敛性，这个“微创”手术刀就是叶果洛夫定理，它最成功的手术案例就是鲁津定理与控制收敛定理；③将微积分中对函数定义域的分割转为对函数值域的分割，不仅大大拓展了可积函数的范围，也使诸如积分与极限交换顺序等问题变得更简单．

（3）筛选可讲可不讲的内容．一些比较浅显，稍加点拨学生便能明白的知识点不必细究，指导学生看书便可．例如，集合的基本运算可以不作详细介绍，仅介绍集合序列的极限概念．集合序列的极限可以从几个维度来介绍：① 为什么会出现集合序列的极限概念？②如何合理地建立这个概念？③这个概念的内涵是什么？它的意义何在？对于诸如此类的重要概念、定理需要浓墨重彩地加以剖析，因为这才是精髓．

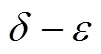
学习能力、数学素养的培养非常重要，教学不能囿于传统的知识体系，要打破常规，围绕着知识体系背后的东西展开教学，这就是思想．因此课堂教学过程中，呈现思想的载体就要有所取舍，选择最能体现思想与最核心的部分．

实变函数课程通常有“集合论”“测度论”“可测函数”“勒贝格积分”等基本章节，有些教材也会介绍“抽象测度”．教师需要根据每一章的内容设计合适的问题，把每一章当成整个课程的子课题．

集合论中关于集合的运算并非难事，难在集合序列的极限以及集合的势（基数）．集合因什么而产生？其间发生了什么事件？为什么会出现集合序列？如何合理地建立集合序列的极限概念？集合序列极限的内涵是什么？把这些问题解决了，实变函数中集合论的主要理论也就建立起来了．

勒贝格测度是建立勒贝格积分的关键，从理论体系看，它与抽象测度大同小异，所不同者，抽象测度会涉及到测度的分解理论，无论是多学时还是少学时的实变函数，在这一章都应该围绕着几个关键问题展开．

●如何度量欧氏空间中的一般集合？

●给出的这种度量合理吗？回到熟悉的区间或矩形，这个度量与传统的度量是否一致？

●这个度量是否继承了传统度量（长度、面积）的所有特征？

●是不是所有集合都可以度量？都具有这样特征？

●可以度量的集合具有什么结构？

由于在开篇科普了勒贝格积分的思想，这一章首先要解决的一个问题便是如何度量一个集合？问题是自然出现的，但寻找合适的度量方法却很不平凡，需要有对黎曼积分的透彻理解和一定的洞察力．对于尚不习惯主动思维的学生来说，靠他们自己来发现无疑是天方夜谭，他们即使课前预习过，也未必能搞明白为什么那样度量集合．这就需要教师深入分析黎曼积分的定义，由于一般的集合无法像曲边梯形那样将函数的定义域分解成一些小区间从而得到一些小矩形条，它可能不含任何矩形（例如有理数集），合适的改进方法是什么？如果学生预习过，自此就明白教材为什么那样定义外测度了．如果没有预习，就要进一步提示，如何改进黎曼的方法，将定义域的分割改成用矩形外包替代，这就是外测度的来历．

有了度量方法，接下来需要研究的问题自然是：它是不是研究者所要的度量？换言之，它是否满足“长度”“面积”以及“体积”的固有特征？分析后发现远没有想象的那么简单，出现了不满足“长度”特征的集合——不可测集．不可测集的构造是天才的杰作，试图独立自主寻找构造的灵感恐怕不现实．有些东西（尤其是反例）是智慧的结晶，有时没有道理可讲．出现了不可测集使得问题变得复杂化了，正如微积分只能处理黎曼可积函数一样，测度论只能处理可测集，导致不可测的原因是什么？是外测度的具体构造方法带来的还是外测度本身固有的？从反例可以看出，不可测集的出现与测度的具体构造无关，换言之，无论你如何定义集合的度量，只要它满足度量的几个基本特征（非负性、单调性、次可加性），总会有一些集合是不可测的，所以只能将这些集合排除出去．

课题进行到这里才真正进入高潮：如何给出一种标准来判断一个集合可测或不可测？黎曼积分能带来什么启发？显然，黎曼的大和与小和可以借鉴过来作为一种判断方法．这种判断方法的优劣之处是什么？如何寻找更合适的判断标准？

课堂正是在这样一个又一个环环相扣的问题中展开的，所有的结果都是在分析问题的过程中得出的，所以无论是结果的先后还是证明的逻辑顺序都有别于教材．课堂可以根据课时决定精雕细琢还是粗线条．

从黎曼大和与小和出发的确可以启发学生通过引入内测度作为判断集合可测的标准，但这个标准有两个缺陷： ①推广到高维时有点麻烦，因为一维时开集有结构性定理，由此结构性定理很容易定义内测度，而到了高维时就要再次讨论开集的结构；②内外测度的可操作性不强，换言之，用它来判断集合的可测性尤其是可测集性质的证明有点繁琐．如何寻找更合适的判定方法？

有了分割性条件之后该做什么？建立一个概念后首先要做的事自然是辨析：它与研究者熟悉的对象之间是什么关系？或者说，研究者熟悉的那些集合是否可测？可测集是否的确具有与“长度”“面积”“体积”类似的特征？在这个分析过程中，所有结论的发现与教材并不完全一致，甚至有时候要采用“插叙”或“倒叙”的方式．例如在讨论可测集对可数次并运算封闭的性质时并不似教材那样按部就班地先讨论互不相交的集合再讨论一般集合，而是通过对一般性问题的分析，发现解决问题的关键．在集合不相交时可加性是否成立，转而讨论不相交集的测度可加性，顺序正好是反过来的．

对于可测集的极限运算也是如此，课堂上不是从特殊集合序列（单调集列）出发，而是直接面对最一般的情形，通过上下极限的讨论，发现问题归结到对单调集列的讨论，从而回到对特殊集列的讨论上来．搞清楚特殊集列后，一般的集列自然就清楚了．

纵观勒贝格测度，其逻辑线条非常清晰，勒贝格积分的定义带出了欧氏空间中一般集合的度量问题，改进黎曼积分的分割求和方法得到了外测度，通过外测度与“长度”的类比发现了不可测集，从不可测集的构造发现不可测集与测度的具体构造无关，仅与外测度固有的特征（非负性、单调性、次可加性）有关，可见这是不可逾越的障碍！只能将不可测集剔除．进而带出了如何判断可测性的问题，于是出现了内测度与卡氏分割性条件．这个条件是不是判断可测性的合适条件？换言之，满足这个条件的集合是不是就是研究者要的可测集？可测集对于集合的运算（包括极限运算）是不是封闭的？测度与极限可否交换顺序？当这些问题搞清楚后，最后的问题便是：这些集合到底是什么？从勒贝格测度的构造性定义能看出什么？把这些问题搞清楚，对勒贝格测度理论的来龙去脉基本就有了一个全局的了解．

假如勒贝格测度没有诞生，拟个相关课题，取一个什么样的题目合适？也许叫做“R中集合的度量”比较合适．上述问题逻辑关系清晰，搞清楚这些问题，测度理论也就建立起来了，这就是从课题研究的视角看测度．

在可测函数章节，由于勒贝格积分的定义中出现了形如{|<()≤}的集合，故提出下面一个自然的问题．

（1）这些集合是否可测？

由此可见，在课程的开篇宏观上介绍一下勒贝格积分理论的来龙去脉是必要的，这为后续各章节的讨论提供了逻辑基础．有了合适的定义，接着便是概念的辨析．

（2）可测函数与熟悉的函数是什么关系？

考察这个问题有两个角度，一个角度是来自微积分的连续函数，这正是该章后半部分需要研究的问题，另一个角度则是基于函数与集合的关系，从这个角度研究时首先需要将黎曼积分的大和、小和转换成实变函数的语言重新表述，即将分割区间得到的和看成小区间对应特征函数的线性组合（分段函数）的积分，这是理解“可测函数是简单函数极限”的基础，也是理解后续介绍的勒贝格积分为什么可以有两种定义方式以及两种方式为什么等价的基础．

（3）一个处处收敛或几乎处处收敛的函数序列与一致收敛性差别有多大？

在对这个问题的分析中涉及一个实变函数中非常重要的思想方法，如何将函数序列不收敛的点用集合的语言表示出来？如何从这个表示中剔除不一致收敛的点集？而且还要保证被剔除的点不能太多（测度可以充分小）．这个思想方法堪称实变函数的精髓，不仅对沟通可测函数与连续函数关系以及勒贝格积分中控制收敛定理的证明至关重要，在很多现代数学理论中也是很常用的思想方法．

另一个精彩的定理是沟通微积分与实变函数关系的桥梁——鲁津定理．它源自下面一个很自然的问题．

（4）可测函数与连续函数的差别有多大？

鲁津定理的重要性是不言而喻的，没有这个定理，便无法建立可测函数与微积分之间的关系．傅立叶分析、调和分析等理论的产生也无从谈起．

集合论、测度论、可测函数都是因勒贝格积分理论的建立不可避免要触及的，有了这些准备之后，就可以呼应课程开始时的勒贝格积分理论介绍中面临的问题了．

●如何建立新型的积分？

●勒贝格积分与黎曼积分是什么关系？

●勒贝格积分是否具有与黎曼积分类似的性质？

●什么样的函数是勒贝格可积的？

●函数序列的极限与积分何时可以交换顺序？

其中也包括黎曼可积函数是什么样的函数等微积分遗留下来的问题．所有这些问题解决之后便圆满完成了课题的研究，课堂教学过程也就完成了．

课题式教学不仅一改以传授知识为主的经典教学方式，而且极大增加了课堂教学的弹性，无论是少课时还是多课时的课程都可以按照这样的模式开展教学，对于少学时课程可以采取粗线条的方式，但需要学生课后花更多的时间，对于多学时课程，则可以围绕着问题深入剖析，细节化展示概念、定理的建立过程，这才是真正意义上数学的再创造．

3 测度论课题式教学案例

勒贝格测度是实变函数课程的重要组成部分，它不仅对于可测函数与勒贝格积分理论具有举足轻重的意义，自身也是数学的一个十分重要的分支．尽管此前已经有若当测度、波雷尔测度，并且这些测度仍然被经常使用，但这些测度与勒贝格测度相比都有着与黎曼积分类似的缺陷：它们都是不完备的．勒贝格积分恰恰克服了这一缺陷，而且为抽象测度奠定了基础．概率论正是建立在抽象测度基础上的，由此可见勒贝格测度的重要．

讲授式教学往往停留在知识传授的层面，讲清楚测度的概念及其基本性质就可以了，但勒贝格测度为什么产生？它的意义与价值是什么？课堂应该围绕着什么进行？这是测度论课堂教学中应该思考的问题．

实变函数课程与其它很多课程一样，学时数由原来的72学时削减到了64学时甚至32学时不等，在如此少的学时数内如何在保证质量的前提下完成该课程主要内容和思想的教学？这是个大难题．能不能找到一种合理的方法在32课时的时间内不降低课程要求的情况下完成该课程的完整教学？如果像往常一样按部就班进行教学，最多讲授到可测函数章节就差不多了，如果似走马观花过一遍，学生学到的实变函数必然流于肤浅，有没有一种两全其美的方案？这正是课题式教学的初衷．多次实践证明，采用课题式教学是兼顾课时与课程完整性的行之有效的方法．课题式教学的心脏是问题，如何发现问题、如何判断问题的科学价值、如何分析问题与解决问题是课题式教学的内核．数学思想正是在分析问题的过程中得以展现，学生的数学直觉、数学审美、思辨、演绎与计算以及数学的价值判断能力也将在这个过程中得到培养与提升．

欧氏空间R中测度论的建立至少需要解决如下几个问题：

●在R中，如何度量一个集合的大小（外测度概念的建立）？

●外测度是不是我们需要的度量方式（不可测集的发现）？

●可测集的判断标准是什么（内测度的发现及卡氏分割性条件的建立）？

●可测集是否具有与经典的长度、面积与体积类似的特征（可测集的性质）？

●可测集的外延有多大（可测集的结构）？

把上述问题解决了，测度论也就建立起来了，这就是所说的课题式教学．实际的课堂教学围绕着下列问题展开．

在一维、二维、三维欧式空间中，常用的度量方式是区间的长度、平面区域的面积和空间立体的体积．但这种方式并不适用于一般的集合，比如Cantor三分集．那么一般的集合应该如何度量呢？

这个度量方式是否合理呢？至少需要从两个维度来考量：① 新的度量方式是否能涵盖原来的度量方式？换言之，对于区间、矩形或长方体，新旧两种度量是不是一致的？ ②长度、面积或体积的性质是否被继承了下来？长度、面积和体积具有哪些共同特征？不难抽象出这3个概念的几个共同特征：非负性、单调性以及可加性．那么Lebesgue外测度是否也具有这3个性质？

根据Lebesgue外测度的定义，非负性和单调性几乎是显然的，外测度的“次（可数）可加性”也不难得到，即

从上述勒贝格不可测集的反例可以看出，勒贝格测度并不总具有可数可加性．但这个性质不仅是经典的长度、面积与体积的本质特征，也是黎曼积分的本质特征之一，正因为面积具有可数可加性，才能采取先分割再叠加求和，进而求极限，再求出黎曼积分．那么，出现上述问题的根源是什么？是外测度构造方法的问题，还是外测度固有的问题？从演算可以看出，演绎过程与外测度的具体构造无关，只要外测度满足非负性、单调性与次（可数）可加性，便总有一些集合不满足（可数）可加性．唯一能做的便是将这些集合排除在外，把他们称为不可测集，只考虑那些具有可加性的集合．问题是，如何判别集合是否可测（满足可加性）？这就自然带出了下面的问题．

问题2：什么样的集合具有测度（可数）可加性？如何判定？

从逻辑上看，这个定义的引入是自然的，但从卡氏分割性条件很难看出可测集内在的结构与性质来．因此需要回答下面几个基本问题．

●常见的集合是不是可测的？

●可测集与通常的长度、面积、体积概念是不是相容的？

●可测集对于集合的运算是否封闭？

●它是否的确满足可加性？

除了长方体体积与测度是否相等的问题稍显麻烦，上述问题的解答几乎是平凡的，但他们的确可以帮助学生对可测集有个初步的体验，了解这个概念符合人的直觉．但在回答开集、闭集是否可测这个问题之前，需要先回答上述4个问题中的后两道，即可测集的性质，于是自然转入了对下列问题的研究．

问题3：可测集是否对集合的运算封闭？对集合的极限运算呢？

图1 两个可测集的并

证明两个集合的情形后，可测集关于集合并、交、差、补运算的封闭性很容易推广到有限个的情形，即

根据集合序列极限的定义以及可测集对集合运算的封闭性很容易看出可测集序列的极限仍然是可测的．但有一个问题并不平凡．

问题4：可测集序列的极限与测度是否可以交换顺序？

从集合序列的极限定义可以看出，如果能对单调集列搞清楚这个问题，一般情形也就不困难了．

图2 可数个可测集的并

上述证明与反例都是在分析过程中逐步寻找到的，这也是数学研究的常规方法，对于提升学生分析问题并在分析问题的过程中找到解决问题方法的能力无疑是有益的．

从上述分析可以看出，分析过程与证明过程的顺序是不同的．课堂是对教材证明的解读，教学过程是对隐藏在表象知识背后思想的挖掘，通过这个分析过程不仅帮助学生理清了教材中定理证明的思路，更重要的是教学生学会通过对问题的探索，有逻辑地思考问题．

至此上述4个问题得到了完满的解答，但还有一个重要问题尚需要回答，这就是可测集的结构问题．

问题5：可测集具有什么样的结构？

进一步，一般的可测集具有何种结构？外测度无疑为这个问题的分析提供了线索．采用开集与闭集互补的关系，也可以从内部用Borel集按测度逼近可测集，具体做法不妨让学生课后自己研究解决．

解决了上述5个基本问题，勒贝格测度论就基本建立起来了．

4 总结

实践证明，课题式教学法是实现弗赖登塔尔“数学教育是数学的再创造”理论的有效途径（参见[4]），但诚如研究者在[5]中所说：“数学教育是数学的有限再创造”，在学生知识积累与认知能力都有限的情况下，需要教师的有效引导才能实现这种再创造．课题式教学使得整个课堂围绕着问题展开，教学过程充满了思辨，这对于培养学生的数学思维能力是至关重要的．同时，课题式教学使得课堂具有了足够的弹性，教师始终围绕着促使概念、定理产生的核心问题展开教学，除了概念的辨析，对定理的详细证明过程则可根据学情与课时的充裕程度决定是否完整给出．

课题式教学的好处是可粗可细，所谓“粗”指的是教师围绕着主要问题展开，略过枝节性的问题；所谓“细”是指在分析问题的基础上详细给出定理的证明．这样的课堂教学需要学生的有力配合，课时不足的情况下，教师只能粗，而学生则需要在课外花更多的时间，因为要掌握一门课程，适当的时间是必不可少的．课内不够只能课外补，教师的任务则是帮助学生解决课程的难点以及透过书本表象知识看清本质，即挖掘隐藏在知识背后的问题、思路和方法，这就是知识所反映的数学思想．只有师生的共同配合与努力，才能真正完成好一门课程的课题式教学．

[1] 曹广福，刘丹．课题式教学法探析[J]．数学教育学报，2020，29（3）：32-36．

[2] 华东师范大学数学系．数学分析（上册）[M]．北京：高等教育出版社，2016：202-203．

[3] 曹广福．实变函数论与泛函分析（上册）[M]．北京：高等教育出版社，2011：31-35．

[4] 弗赖登塔尔．作为教育任务的数学[M]．陈昌平，唐瑞芬，译．上海：上海教育出版社，1999：107-110．

[5] 曹广福，张蜀青．问题驱动的中学数学课堂教学（理论与实践卷）[M]．北京：清华大学出版社，2018：103-104．

Project-Based Instruction for Real Variable Functions

CAO Guang-fu

(School of Mathematics & Information, South China Agricultural University, Guangdong Guangzhou 510642, China)

Project-based instruction can effectively deal with the tension between the entirety of content coverage in a course and insufficient allocation of time for the course. Project-based instruction of the real variable functions first needs to guide students to understand the historical development of the real variable function and the usefulness of applying them to solve problems faced. It requires of identifying big ideas in real variable functions and understand major thought processes. Through presenting a teaching case of measure theory, this paper explains how to actually design and deliver project-based instruction. Through the teaching case, it emphasized not only the facilitation of fostering students’ problem posing, but also identifying the value and importance of the posed problems, hence, help students to learn how to reason and think mathematically.

Lebesgue measure; measurable function; Lebesgue integral; project-based instruction

G642

A

1004–9894（2021）02–0032–06

曹广福．实变函数课题式教学研究[J]．数学教育学报，2021，30（2）：32-37．

2020–10–09

国家“万人计划”人才项目——问题驱动的数学课堂教学理论与实践；国家应用数学中学粤港澳大亚湾应用数学中心项目——问题驱动的中小学数学教育研究（2020B1515310020）

曹广福（1960—），男，江苏海安人，教授，博士生导师，首届国家教学名师，入选第二批国家“万人计划”教学名师，主要从事数学研究与数学教育研究．

[责任编校：陈隽、陈汉君]