高中学生数学原有知识水平和学习认知负荷对数学课堂学习效率的影响研究

马淑杰，张景斌

高中学生数学原有知识水平和学习认知负荷对数学课堂学习效率的影响研究

马淑杰1，张景斌2

（1．首都师范大学 教育学院，北京 100048；2．首都师范大学 教师教育学院，北京 100048）

数学学习效率一直是教育研究者和一线教师都关注的问题．通过课堂教学实验，探讨高中学生数学原有知识水平和学习认知负荷对数学课堂学习效率的影响．研究结果表明：（1）无论是中等负荷还是高负荷数学内容的学习，学生的原有知识水平都对课堂学习效率存在极其显著性影响．（2）当学生学习中等负荷的数学内容时，学生的学习认知负荷对课堂学习效率存在显著性影响，而学习高负荷数学内容时影响不显著．在剔除掉数学原有知识水平差异的条件下，两种负荷水平内容的学习都表明学生的学习认知负荷对课堂学习效率不存在显著性影响．（3）两种负荷水平数学内容的学习结果都表明：学生数学原有知识水平和学习认知负荷对课堂学习效率没有显著的交互性影响．

高中学生；原有知识水平；学习认知负荷；课堂学习效率

1 问题提出

高效学习是对学生学习和教师教学评价的主要方面之一．事实上，即使是同一个班级的学生，课堂学习效率也会有很大差异．学习效率问题受到广泛的关注，很多一线教师和教育研究者对其进行了大量研究，这些研究多是从教育学、学习心理学、社会学等角度进行的质性探索，John Sweller提出的认知负荷理论为研究者用实证的方法分析学习效率的影响因素提供了新的视角．

20世纪80年代末，澳大利亚认知心理学家约翰·斯威勒（John Sweller）提出认知负荷理论（cognitive load theory，CLT）．该理论直接建立在信息加工心理学的基本概念基础之上，以认知资源有限理论和图式理论为基础，从资源分配的角度来考察学习和问题解决．认知负荷理论认为：问题解决或学习过程中的各种认知活动均需要消耗认知资源，若所有活动所需要的认知资源总量超过了个体所具有的资源总量，则存在资源不足的问题，从而影响学习或问题解决的效率[1]．认知负荷理论作为认知加工和教学设计的主要框架理论，越来越受到人们的关注．

Sweller等人根据影响认知负荷的主要因素，将认知负荷区分为内在认知负荷（ICL）、外在认知负荷（ECL）和相关认知负荷（GCL），3种认知负荷的总和就是认知负荷总量，即总认知负荷（TCL）[2–3]．

内在认知负荷是由学习材料的内在特征施加给学习者工作记忆（工作记忆是一种对信息进行暂时加工和贮存的容量有限的记忆系统，在许多复杂的认知活动中起重要作用）的负荷，它一般是由学习材料的复杂性及与之相联系的学习者先前知识经验等因素引起[2]．Seufert等人又把内在认知负荷做了进一步的分类，其中把由学习材料的复杂性引起的这种由外部因素决定的内在认知负荷称为外因决定的内在认知负荷；由于学习者先前知识经验会影响认知图式的可获得性，从而影响认知负荷，因此，把这种由学习者内部因素决定的内在认知负荷称为内因决定的内在认知负荷[4]．

外在认知负荷是由学习材料的组织与呈现方式给工作记忆带来的认知负荷，它由学习过程中对学习没有直接贡献的心理活动引起．当要求学习者从事一些与图式获得或自动化没有直接关联的活动时便会产生外在认知负荷．大量研究表明，外在认知负荷对学习没有积极作用，有时甚至会阻碍学习，因此也称为无效的认知负荷．

相关认知负荷就是学习者在完成某一任务的过程中，把未用完的剩余认知资源用到与学习直接相关的加工时所产生的认知负荷[6]．也就是说，相关认知负荷并不是由学习材料本身所引起的．如果学习者学习时的内在认知负荷较低，使得学习者还有充分的认知资源可用，这时他就可以投入额外的一部分认知资源来促进图式的建构．这种在建构图式时不是必须但投入后又有利于图式建构的认知负荷，就是相关认知负荷．

Sweller等人（1998）通过研究指出，学习者关于特定任务的能力和原有知识经验会影响完成任务的内在认知负荷[2]．也就是，对于给定的任务，如果学习者在长时记忆中没有足够的与之相关的知识经验，则在理解和完成任务时就会给工作记忆增加负担，从而产生较高的认知负荷．Sweller等人（1999）通过对综合性较强的知识领域的学习研究指出，将综合领域知识分割成互不影响的各组成成分能够减少认知负荷，从而提高学习效率[7]．Valcke（2012）的研究表明，如果学习者有着丰富的、高水平的知识经验，也就是，其在长时记忆中存储的图式更容易被提取到工作记忆中充当新知识学习的先行组织者，帮助处理感知到的信息，因此，能够降低工作记忆的负担，从而有效减少认知负荷[8]．可见，以往关于认知负荷与学习的研究中，关于学习者原有知识水平与学习认知负荷的研究有较一致的结论，即对于某一给定任务的学习中，学习者高水平的原有知识经验能够有效减少学习的认知负荷，而学习认知负荷的高与低又直接影响学习效果[5]．

一方面，以往研究结论大多数是在有高度控制的实验室研究基础上得出的，而实验室与真实课堂学习情境之间存在较大的差异．在日常课堂教学情境中，当高中学生学习具有不同内在认知负荷的数学材料时，上述结论是否同样成立？另一方面，以往研究结论指出对于某一给定任务的学习，学习者高水平的原有知识经验能够有效减少学习认知负荷、学习认知负荷的高与低又直接影响学习效果．那么高中学生数学先前知识经验水平的差异、学习认知负荷的差异对数学课堂学习效率是否具有显著性影响？影响是否具有交互性？这些问题都是在真实的课堂教学情境中进行探索的问题，以期为高中数学教师更好地进行教学设计提供依据，进而有效提升学生数学课堂学习效率[9-13]．

2 研究方法

采用教学实验的方法，共开展了两个数学课堂教学实验，定量研究学生原有知识水平和学习认知负荷对课堂学习效率的影响．

（1）被试．

北京市某中学高一、高二年级的学生．其中实验1的被试是高二年级3个平行班共112名学生，年龄均在16~17岁之间．实验2的被试是高一年级6个平行班共209名学生，年龄均在15~16岁之间．

学生原有知识水平分组，是将学生原有知识水平测试得分按升序排序，利用极端分组法，将学生分为低、中和高原有知识水平组．依据极端分组法，排序前、后各27%应分别为低原有知识水平组和高原有知识水平组，实际操作中由于学生出现分数并列情况，最终实验1中低原有知识水平组有学生35人，中等原有知识水平组有学生46人，高原有知识水平组有31人；实验2中低原有知识水平组有学生59人，中等原有知识水平组有学生83人，高原有知识水平组有67人，具体分组情况见表1．

表1 被试原有知识水平和学习认知负荷分组

学生学习认知负荷是指学生在学习任务完成过程中进行信息加工所耗费的认知资源总量，其大小用Pass编制的认知负荷自评量表测定．学生学习认知负荷水平分组，是根据学生学习认知负荷实际测量结果的平均值，结合认知负荷测量理论均值（总分为9，理论均值为4.5），并参考极端分组法确定的．实验1中，学生学习认知负荷实际测量结果的平均值为4.54与理论均值非常接近．实际操作中将学习认知负荷不高于3.5的学生定义为低学习认知负荷水平学生，共有37人，认知负荷区间是[1.5, 3.5]；将学习认知负荷在区间[4, 5]范围内的学生定义为中等学习认知负荷水平学生，共44人；将学习认知负荷不低于5.5的学生定义为高学习认知负荷水平学生，共有31人，认知负荷区间是[5.5, 7.5]．实验2中，学生学习认知负荷实际测量结果的平均值为5.56，高于理论均值1.15，理论上可以认为实验2为高认知负荷学习．为了在实验中对被试学生群体的学习认知负荷水平进行划分，实际操作中将学习认知负荷不高于4的学生定义为低学习认知负荷水平学生，共22人，认知负荷区间是[1, 4]；将学习认知负荷在区间[4.5, 6]内的学生定义为中等学习认知负荷水平学生，共122人；将学习认知负荷不低于6.5的学生定义为高学习认知负荷水平学生，共65人，认知负荷区间是[6.5, 9]．两个实验的学生原有知识水平分组和学习认知负荷分组均满足正态分布，正态分布的平均值和标准差以及具体分组情况见表1．

（2）材料．

材料1：两个实验的课堂教学内容均选自人教A版教材，其中实验1为选修2–3中“独立重复实验与二项分布”．实验2为数学必修2中“立体几何证明中的存在性问题”．实验中学习材料引起的内在认知负荷（用表示）界定为：学习材料包含的元素数量（用字母表示）、学习者需要同时关注的元素间关系数量（用表示）和出现的产生式（产生式是一些“条件—行动”对，即“如果—那么”的规则）数量（用表示）的总和，用公式表示为：=++．其中产生式数量代表材料中所涉及到的程序性知识的数量．按照上述公式，计算出实验1和实验2的学习材料引起的内在认知负荷总数分别为296和502．实验中，将实验1和实验2分别界定为中等负荷材料的学习和高负荷材料的学习．

材料2：Pass编制的认知负荷自评量表．该量表包括心理努力（心理努力是认知负荷的重要指标，是指对活动实际投入的认知资源的多少）和任务难度评价两个维度，每个维度均采用9级评分制，要求被试在完成学习任务后，根据自己的感受，从1—9中选择一个合适的数字．从1—9表示付出的心理努力和材料难度依次递增，1表示付出最少努力、任务非常容易，5表示中度努力、中等难度，9表示非常努力、非常困难．学生学习认知负荷是两个维度的算数平均值．该量表的内部一致性信度系数为0.74．

材料3：学生原有知识水平测试卷．学生原有知识水平是指学生学习新内容前所必备的先前基础知识、基本技能和数学思想方法．研究中，根据新知课学习对原有知识经验的要求，设计全面考查学生原有知识水平的测试题目，最终用学生的测试得分代表其该节课学习的原有知识水平．

材料4：学生课堂学习效率测试卷．在课堂教学中学生获得有效知识量的多少就是学生课堂学习效率问题．课堂学习效率是指：学生在一节课（45分钟）的学习中，所掌握的知识、方法和技能以及数学思想．用学生学习的及时后测成绩作为学习效率的评价指标．实验中及时后测试卷是根据教学目标，结合教学基础知识、例题和练习等所涵盖的知识、技能以及思想方法等设计后测试题，全面考查学生该节课学习的掌握情况．

（3）程序．

研究中两个课堂教学实验研究的实施程序都分三步进行，分别是实验前测（学生原有知识水平测试）；以讲授法为主开展课堂教学，并在当节课结束时随即组织学生进行学习认知负荷测试（Pass量表）；课堂学习及时后测．其中前测是在课堂教学实验前一天统一进行，后测是在学生学习认知负荷测试结束后进行，测试时间为30分钟．测试均有老师专门组织和指导，能够确保成绩真实有效，并做到按时发放和收回测试卷或量表．

（4）数据分析．

实验前测、后测和学习认知负荷测试数据收集后，利用SPSS22.0统计软件对数据进行统计分析．

3 结果

（1）学生原有知识水平对课堂学习效率的影响．

将学生原有知识水平作为自变量，课堂学习效率作为因变量，借助于单因素方差分析及事后多重比较，分析不同原有知识水平组学生之间的课堂学习效率差异．

学生原有知识水平对课堂学习效率的描述性统计分析结果表明（表2）：无论学习中等负荷水平的学习材料还是高负荷学习材料，学生的课堂学习效率都随着学生原有知识水平提高呈现单调递增，即学生的原有知识水平越高，课堂学习效率越高．而且，单因素方差分析结果显示：不同水平原有知识组之间学生的课堂学习效率均存在极其显著的差异（=0.000***）．

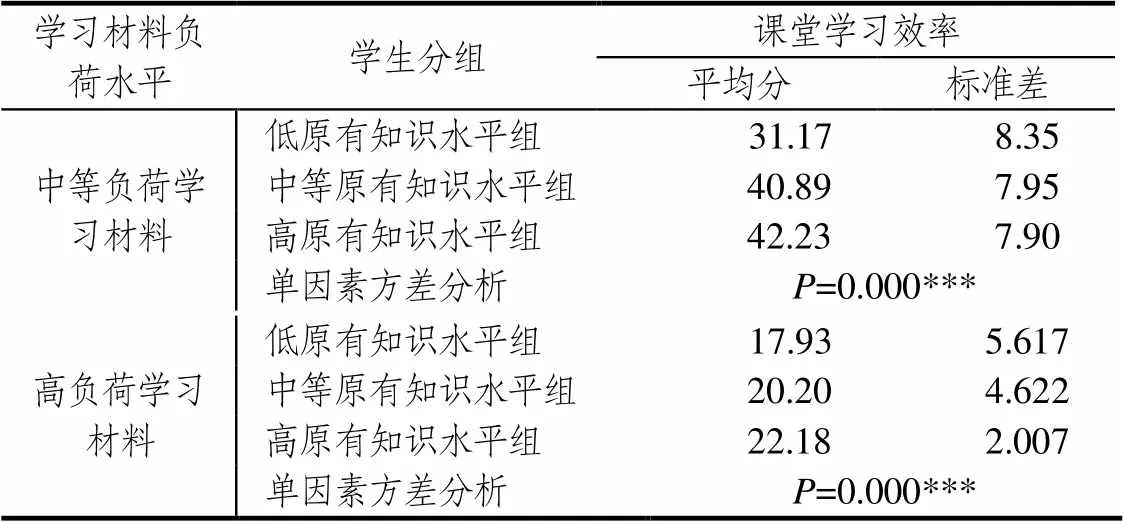
表2 学生原有知识水平对课堂学习效率的影响

注：*＜0.05，**＜0.01，***＜0.001（下同）

特别的，单因素方差分析事后多重比较结果表明：对于高负荷材料的学习，3个原有知识水平组之间学生的课堂学习效率均存在非常或极其显著的差异，其中低与中原有知识水平组学生之间课堂学习效率差异的显著性为=0.002**，低与高、中与高原有知识水平组学生之间课堂学习效率差异的显著性分别为=0.000***和=0.006**．而中等负荷材料的学习，高原有知识水平组和中原有知识水平组学生的课堂学习效率均与低原有知识水平组之间存在着极其显著的差异（=0.000***）．但是高原有知识水平组与中等原有知识水平组之间学生的课堂学习效率差异不显著（=0.478）．

（2）学生学习认知负荷对课堂学习效率的影响．

将学生学习认知负荷水平作为自变量，课堂学习效率作为因变量，借助于单因素方差分析及事后多重比较，分析不同学习认知负荷水平组学生之间的课堂学习效率差异（表3）．描述性统计结果表明：随着学生学习认知负荷的提高，课堂学习效率呈现单调递减，即学生学习认知负荷越高，课堂学习效率越低，且这一结果与学习材料的负荷等级无关．单因素方差分析结果表明，对于中等负荷材料的学习，不同学习认知负荷水平组学生的课堂学习效率存在非常显著的差异（=0.007**）．而高负荷材料学习时，不同学习认知负荷水平组学生的课堂学习效率没有显著性差异（=0.223）．

单因素方差分析多重比较结果表明，对于中等负荷内容的学习，低学习认知负荷水平组学生与中、高学习认知负荷水平组学生的课堂学习效率均存在非常显著的差异，显著性分别为=0.009**和=0.005**；但是中等学习认知负荷水平组与高学习认知负荷组学生的课堂学习效率差异不显著（=0.641）．当学生学习高负荷内容时，低、中、高3个学习认知负荷水平组学生的课堂学习效率均不存在显著性差异，其中低与中学习认知负荷组学生课堂学习效率差异的显著性为=0.208，低与高、中与高学习认知负荷组学生的课堂学习效率之间差异的显著性分别为=0.085和=0.384．

表3 学生学习认知负荷水平对课堂学习效率的影响

（3）学生原有知识水平和学习认知负荷对课堂学习效率影响的多因素方差分析．

学生原有知识水平和学习认知负荷对课堂学习效率影响的多因素方差分析主体间效应检验结果（表4）表明：无论是中等负荷材料的学习还是高负荷材料的学习，学生原有知识水平对课堂学习效率都具有极其显著的影响（=0.000***），而学生学习认知负荷水平对课堂学习效率的影响却不显著（中等负荷材料学习=0.130；高负荷材料学习=0.749）．值得关注的是，这一结果与表3是有差异的，原因是多因素方差分析是在剔除了其它控制变量，即剔除原有知识水平差异影响下的学生学习认知负荷对课堂学习效率的影响．特别地，学生原有知识水平和学习认知负荷没有对课堂学习效率产生显著的交互性影响（中等负荷材料学习=0.748；高负荷材料学习=0.684）．

借助于图形可以更加直观地了解学生原有知识水平和学习认知负荷两个因素对课堂学习效率的交互作用．图1和图2分别是中等负荷和高负荷材料学习中学生原有知识水平和学习认知负荷对课堂学习效率交互作用的分析图形．

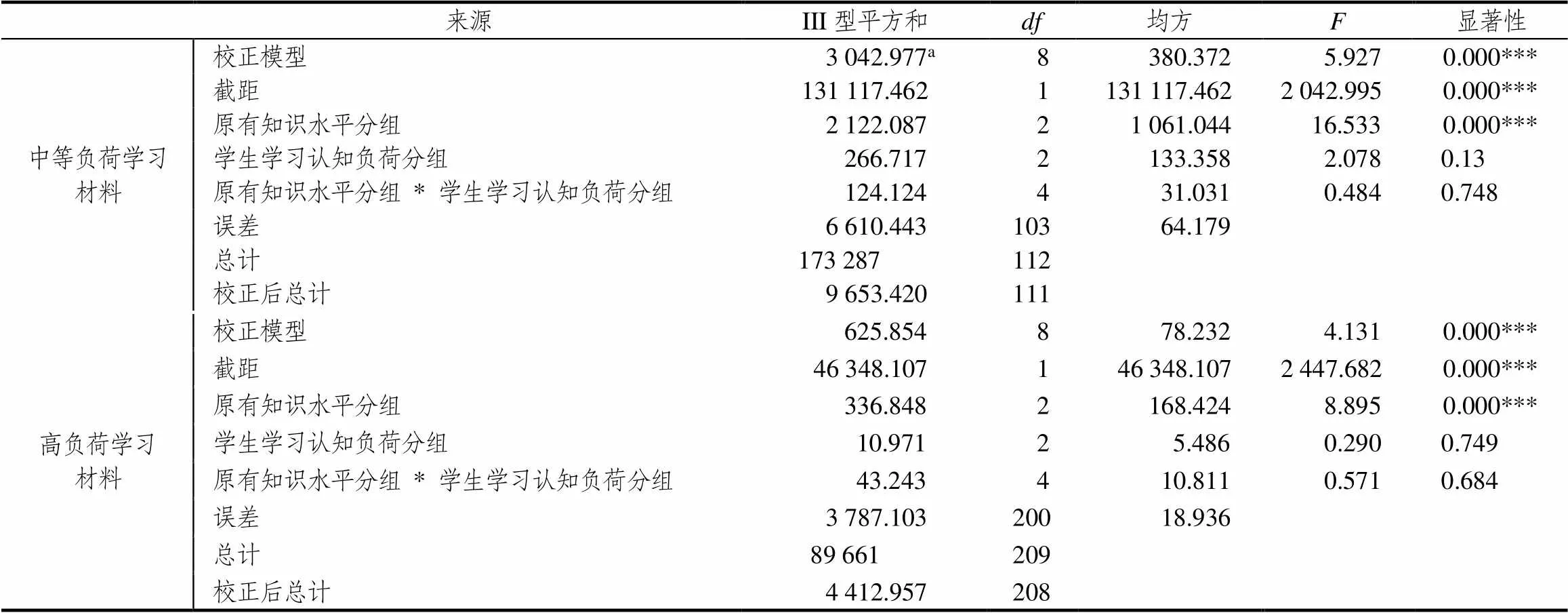
表4 学生原有知识水平和学习认知负荷对课堂学习效率影响的多因素方差分析主体间效应检验

图1 中等负荷材料学习

图2 高负荷材料学习

从图1可以发现，对于中等负荷材料的学习，低学习认知负荷水平组与中等学习认知负荷水平组学生的原有知识水平和学习认知负荷对课堂学习效率的影响不存在交互作用（两条线的走势基本呈平行趋势）．但是高与中等学习认知负荷水平组的学生，原有知识水平和学习认知负荷水平对课堂学习效率的影响存在一定的交互作用（两条线出现交叉），但是从表4数据看这种交互作用没有达到显著性水平．图2则表明，对于高负荷材料的学习，学习认知负荷3个水平组的学生，原有知识水平和学习认知负荷对课堂学习效率的影响都有一定的交互作用（每两条线有交叉），同样表4数据显示这种交互作用没有达到显著性水平．

（4）学生学习认知负荷对课堂学习效率影响的协变量分析．

由于多因素方差分析结果表明，在剔除掉原有知识水平差异的条件下，学生学习认知负荷对课堂学习效率不存在显著性影响，与单因素方差分析结果出现差异．因此，为了进一步分析学生学习认知负荷对课堂学习效率的影响，研究中借助于协方差分析，将学生原有知识水平作为协变量，分析在剔除原有知识水平差异的条件下，学生学习认知负荷水平对课堂学习效率的影响．表5给出了课堂学习效率的协方差分析主体间效应检验结果，其中学生原有知识水平为协变量．数据表明，对于两种负荷水平的材料学习，在剔除学生原有知识水平差异的条件下，学生学习认知负荷对课堂学习效率均没有显著性影响（中等负荷材料学习=0.078；高负荷材料学习=0.606）．这一结论和多因素方差分析的结果一致，两种不同的分析方法都表明在剔除学生原有知识影响的条件下，学生学习认知负荷水平对课堂学习效率影响不显著．

表5 课堂学习效率的协方差分析主体间效应检验

4 讨论

（1）无论是中等认知负荷还是高负荷材料的学习，实验结果都表明：学生原有知识水平越高，课堂学习效率越高，而且学生的原有知识水平对课堂学习效率有着极其显著的影响．特别的，当学生学习高认知负荷材料时，低、中、高3个原有知识水平组学生的课堂学习效率均存在显著性差异．但是，当学生学习中等负荷的材料时，低原有知识水平组学生的课堂学习效率与中、高原有知识水平组均存在显著性差异，而中等原有知识水平和高原有知识水平组之间的课堂学习效率差异不显著．这可以理解为，当学习材料引起的认知负荷不高时，中等和高原有知识水平组学生都有足够的认知资源参与新知识的学习与构建，都能顺利地完成学习任务，从而使课堂学习效率达到很好的效果，两个组学生的课堂学习效率没有显著性差异．而对于原有知识水平较低的学生，尽管学习材料引起的认知负荷并不高，但是和中、高原有知识水平组学生相比，由于他们长时记忆中没有足够的、活跃的图式用于新知识的学习与构建，相比较而言更容易出现认知超负荷，所以学习效率会显著低于另外两个水平组学生．总之，实验结果表明学生原有知识水平对课堂学习效率均起着决定性作用，这一结果和以往的研究结论基本一致．

（2）两个实验研究结果从宏观上都得到了与以往研究一致的结论，即学生的学习认知负荷越高，课堂学习效率越低．然而，深入分析能够发现和以往研究结论的差异．

一方面，单因素方差结果显示：当学生学习中等负荷的材料时，学生的学习认知负荷对课堂学习效率存在显著性影响，而学习高负荷材料时影响不显著．这一结果用认知负荷理论可以解释为：高负荷材料学习时，无论是处于学习认知负荷低、中、高哪个水平的学生，其学习认知负荷都已经达到理论上的高负荷（学生学习认知负荷实际测量平均值5.56，高于理论均值1.15），学习认知负荷的差异难以对课堂学习效率产生显著性影响．

另一方面，当剔除掉原有知识水平差异的条件下，两种负荷水平材料的学习都表明学生学习认知负荷对课堂学习效率均不存在显著性影响．这一结果可以理解为学生学习认知负荷对课堂学习效率的影响，主要是由学生的原有知识水平引起的．也就是学生原有知识水平的差异导致了学习认知负荷的差异，从而影响课堂学习效率，这进一步说明了学生原有知识水平对学生课堂学习效率的决定性作用．

（3）两种负荷水平学习材料的学习结果都表明：学生原有知识水平和学习认知负荷对课堂学习效率没有显著的交互性影响．但是从图1和图2可以看出，当学习中等负荷的材料时，学习认知负荷高与中水平组学生以及学习高负荷材料时，学习认知负荷低、中、高3个水平组学生之间，学生原有知识和学习认知负荷对课堂学习效率都存在一定的交互作用．这样的结果用认知负荷理论可以解释为：当学生的学习认知负荷不高时（即低、中认知负荷），学生在学习时有足够的认知资源用于新知识的学习和认知构建，此时不易出现认知超负荷．因此，学生原有知识水平和学习认知负荷对课堂学习效率不会产生显著的交互性影响．但是当学生学习处于高认知负荷状态时，学生将出现认知资源不足．和原有知识水平较高的学生相比，原有知识水平较低的学生在其长时记忆中没有足够的、活跃的认知图式参与认知构建，而是将每一个信息元素作为独立于一个单元占用工作记忆的资源，从而导致认知负荷过重，难以顺利进行新知识的有效学习，从而影响课堂学习效率．

5 启示

（1）基于学生原有知识水平进行分层教学设计．

由于学生的原有知识水平对课堂学习效率起着决定性作用，不同原有知识水平学生之间课堂学习效率存在非常显著的差异，因此教师们在进行每一节课的教学设计之前都要认真做好学情分析．学情分析不只是分析学生的认知水平和能力以及学生已经学习了什么，更重要的是基于将要学习的内容对学生原有知识的要求以及学生的实际学习基础情况进行细致的分析．以便在教学设计中针对学生的不同原有知识水平，分层设计概念的形成或呈现方式、例题和习题的选择与改编等，使教学的各环节更加有利于学生认知图式的形成和自动化．基于学生原有知识水平分层设计和实施教学既有利于减轻学生的学习负担，又能形成高效教学．

（2）基于学习材料引发的认知负荷进行教学设计．

学习材料的认知负荷越高，学生越容易出现高负荷学习，从而影响学习效率．因此，教师在教学设计前应该分析材料引发的内在认知负荷水平．特别是，当进行高负荷材料的学习时，要通过创设恰当的问题情境来增加学生的数学基本活动经验，通过分解学习内容难度、精选或调整例题与习题的复杂程度或顺序等控制或分解材料引发的内在认知负荷．与此同时，还要精心设计、优化内容的呈现方式，一方面让材料的呈现更有利于学生认知图式的形成和自动化，另一方面通过优化后的呈现方式来控制无关负荷，从而达到控制认知总负荷、节省学生学习认知资源，最终达到提高学习效率的目的．

（3）教师要转变教学理念．

教师不应只关注自己如何讲得好，而是要更加关注如何才能让不同层次的学生学得好．当教师在教学中发现某个教学内容学生理解或掌握困难时，不要急于抱怨，而是要静下心来分析出现困难的原因，是不是学习内容所引起的认知负荷较高．在分析材料内在认知负荷的过程中，既可以得出材料所引起的内在认知负荷高低，也能够分析出哪个知识点或解题步骤引起的认知负荷大，以便在教学设计时可以将其有效分解，并有意识降低由学习材料的组织和呈现方式引发的外在认知负荷，从而控制认知总负荷，提高课堂学习效率．

总之，教师在进行教学设计和组织教学时，要能够有意识地运用认知负荷理论进行教学设计和实施，从而达到既有利于减轻学生学习负担，又有利于形成高效能教学的目的．

[1] 马淑杰，连四清，冯汝静，等．高中生数学课堂学习效率的个体差异研究[J]．数学教育学报，2009，18（2）：46–48．

[2] SWELLER J, van MERRIENBOER J J G, PAAS F. Cognitive architecture and instructional design [J]. Educational Psychology Review, 1998, 10 (3): 251–296.

[3] PAAS F, RENKL A, SWELLER J. Cognitive load theory and instructional design: Recent developments [J]. Educational Psychologist, 2003, 38 (1): 1–4.

[4] SEUFERT T, JANEN I, BRUNKEN R. The impact of intrinsic cognitive load on the effectiveness of graphical help for coherence formation [J]. Computers in Human Behavior, 2007, 23 (3): 1 055–1 071.

[5] 孙崇勇，李淑莲．认知负荷理论及其在教学设计中的运用[M]．北京：清华大学出版社，2017：29–31，52–54．

[6] SWELLER J. Cognitive load theory, learning difficulty, and instructional design [J]. Leaning and Instruction, 1994, 4 (3): 295–312.

[7] 常欣，王沛．认知负荷理论在教学设计中的应用及其启示[J]．心理科学，2005，28（5）：1 115–1 119．

[8] VALCKE M. Cognitive load, updating the theory [J]. Learning and Instruction, 2012, 12 (1): 47–154.

[9] 吕世虎，于丽芳，王尚志．数学试卷综合难度的内涵及其指标体系建构[J]．数学教育学报，2020，29（4）：1-6．

[10] 郑雪静，陈清华，王长平，等．高中生直观想象素养的测量与评价研究[J]．数学教育学报，2020，29（4）：7-12．

[11] 何声清．“代表性启发”对初中生古典概率内容学习进阶的影响[J]．数学教育学报，2020，29（4）：27-33．

[12] 朱清波，曹广福．例谈探究式解题课教学[J]．数学教育学报，2020，29（2）：49-52．

[13] 吴增生．数学学科核心素养导向下的有理数教学实证研究[J]．数学教育学报，2020，29（2）：53-57．

Influence of High School Students’ Prior Knowledge and Cognitive Load on Their Learning of Mathematics from Classroom Instruction

MA Shu-jie1, ZHAGN Jing-bin2

(1. College of Education, Capital Normal University, Beijing 100048, China;2. College of Teacher Education, Capital Normal University, Beijing 100048, China)

Mathematics learning efficiency has long been a concern of educational researchers and teachers. The experimental results of classroom teaching in this study showed three things. First, for both medium and high cognitive load mathematical materials, the prior knowledge of students had a significant impact on students’ learning of mathematics from classroom instruction. Second, the cognitive load of students’ learning had a significant impact on mathematics classroom learning efficiency when students learned from medium cognitive load mathematics materials. However, the effect was not significant when high cognitive load materials were involved. Learning materials of both cognitive load levels showed that the cognitive load of students had no significant impact on mathematics classroom learning efficiency when prior knowledge differences were controlled in the analysis. Third, learning from both cognitive load levels of mathematical materials showed that students’ prior knowledge level and learning cognitive load had no significant interaction on their learning.

high school students; prior knowledge; cognitive load; classroom instruction, learning outcome

G622

A

1004–9894（2021）02–0026–06

马淑杰，张景斌．高中学生数学原有知识水平和学习认知负荷对数学课堂学习效率的影响研究[J]．数学教育学报，2021，30（2）：26-31．

2020–10–11

北京市教育科学规划重点课题——指向育人价值的高中数学概念教学研究（CDAA2020053）

马淑杰（1976—），女，回族，北京人，高级教师，博士生，主要从事数学学习心理与高中数学教学研究．

[责任编校：周学智、陈隽]