正整数被素数p整除的判别法

管训贵

(泰州学院 数理学院，江苏 泰州 225300)

0 引言

判别一个正整数M能否被某素数p整除这一问题，1963年华宏鸣[1]进行了探讨并证明了命题1和2。

命题1正整数M能被素数p(p≠2,5)整除的充要条件是截去M的末位数后，在十位数上加上末位数的a倍，所得的数能被p整除，其中a满足条件lp+1=10a。更一般地说，有正整数M=10x+y能被素数p整除的充要条件是M′=x+ay能被p整除。

命题2正整数M能被素数p(p≠2,5)整除的充要条件是截去M的末位数后，在十位数上减去末位数的a倍，所得的数能被p整除，其中a满足条件lp-1=10a。更一般地说，有正整数M=10x+y能被素数p整除的充要条件是M′=x-ay能被p整除。

后来，文献[2-6]又相继给出了其他判别法。本文给出一个比较简单的判别法，用以判别一个正整数M能否被某素数p整除。考虑到一个正整数被2和5整除与否，仅需看末位数即可，故不妨设p≠2,5。

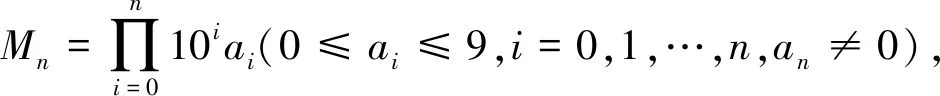
由定理1直接可得推论1、推论2和推论3。

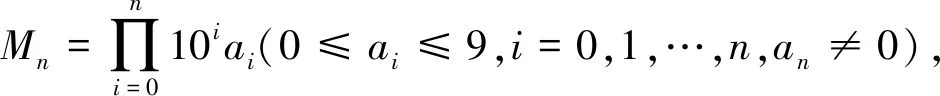
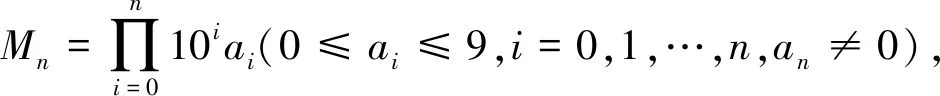
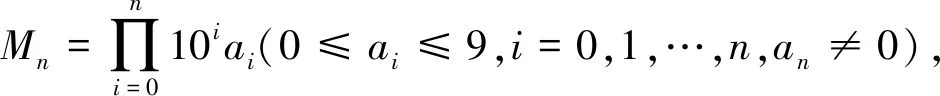
1 定理1及推论的证明

不妨设k>0。先用数学归纳法证明knMn≡bn(modp)。

当k=1时，kM1=k(a0+10a1)=(kc0+a1)+(10k-1)a1≡b1(modp)，结论成立。假设k=l时，结论成立，即klMl≡bl(modp)，则当k=l+1时kl+1Ml+1=kl+1(Ml+10l+1al+1)=k·klMl+(10k)l+1al+1≡k·bl+(10k)l+1al+1≡k·bl+al+1+((10k)l+1-1)al+1≡k·cl+al+1+((10k)l+1-1)al+1≡bl+1(modp)，这说明结论对k=l+1也成立。因此knMn≡bn(modp)。由此知p|(knMn-bn)。因为gcd(kn,p)=1，所以p|Mn⟺p|bn。定理1得证。

另外，当k=2时，10×2≡1(mod 19)，故由定理1知，对∀i=0,1,…,n-1,若bi+1=2ci+ai+1，bi+1≡ci+1(mod 19)，其中c0=a0，|ci+1|≤9，则19|Mn⟺19|bn。推论1得证。

当k=7时，10×7≡1(mod 23)，故由定理1知，对∀i=0,1,…,n-1,若bi+1=7ci+ai+1，bi+1≡ci+1(mod 23)，其中c0=a0，|ci+1|≤11,则23|Mn⟺23|bn。推论2得证。

当k=-3时，10×(-3)≡1(mod 31)，故由定理1知，对∀i=0,1,…,n-1,若bi+1=-3ci+ai+1，bi+1≡ci+1(mod 31)，其中c0=a0，|ci+1|≤15,则31|Mn⟺31|bn。推论3得证。

2 应用举例

例1试证：1)19|9 739 153；2) 31|/19 631 126。

证明1)易知，2×3+5=11，11≡11(mod 19)，2×11+1=23，23≡4(mod 19)，2×4+9=17，17≡17(mod 19)，2×17+3=37，37≡-1(mod 19),2×(-1)+7=5,5≡5(mod 19),2×5+9=19,19|19，所以19|9 739 153。

2) 易知，-3×6+2=-16，-16≡15(mod 31)，-3×15+1=-44，-44≡-13(mod 31)，-3×(-13)+1=40，40≡9(mod 31)，-3×9+3=-24，-24≡7(mod 31)，-3×7+6=-15，-15≡-15(mod 31)，-3×(-15)+9=54，54≡-8(mod 31)，-3×(-8)+1=25，31|/25，所以31|/19 631 126。

例2判别5 870 699能否被23整除。

解易知，7×9+9=72，72≡3(mod 23)，7×3+6=27，27≡4(mod 23)， 7×4+0=28，28≡5(mod 23)，7×5+7=42，42≡-4(mod 23)，7×(-4)+8=-20，-20≡3(mod 23)，7×3+5=26，23|/26，所以5 870 699不能被23整除。

说明如果在定理中取k=1,-2,-1,4,-5,3,-11,-4,13,-14,16,6,-6,-20,-7,22,8,25,9,-29，还可以得到被素数p=3,7,11,13,17,29,37,41,43,47,53,59,61,67，71,73,79,83,89,97整除的判别法(以上得到了100以内除2，5以外的全部素数的整除性判别法)。由于gcd(10,p)=1，即同余方程10k≡1(modp)总是有解的，故本定理涵盖了被任意素数p整除的判别法。