运输位势经济意义研究

石磊昊

(中国人民解放军陆军特种作战学院 军政基础系，广西 桂林 541002)

0 引言

运输问题对于提高线性规划问题解决实际问题的能力以及军事运输问题的实际规划都有十分重要的意义[1]。在运输问题的求解过程中，最优性检验是实现优化的重要依据，因此，运输问题最优性检验的理解对于学习和掌握运输问题至关重要[2]。

1 运输问题及其最优性检验

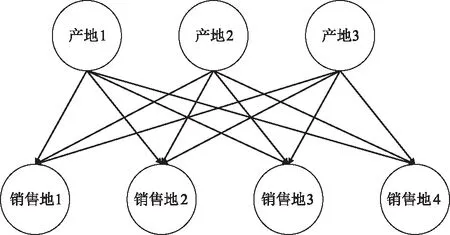
图1 运输问题概念模型 Fig.1 Conceptual model of transportation problem

在军事运筹学中，运输问题泛指在调拨运输各类物资(如武器弹药)的实际活动中，根据现有交通情况，制订合理的运输方案，使总的运输代价最小的一类问题[3]。一般运输问题包含多个产地和多个销售地，其概念模型可用图1表示。在运输问题中，根据产地供应量和销售地需求量之间的关系，可以分为“供求平衡的运输问题”(以下简称“平衡的运输问题”)和“供求不平衡的运输问题”(以下简称“不平衡的运输问题”)。

1.1 运输问题的数学模型

在运输问题的实际解决过程中，由于不平衡的运输问题都可以转化为平衡的运输问题进行解决，因此，本文仅以平衡的运输问题为研究对象。

对于平衡的运输问题，其数学模型可以表示为

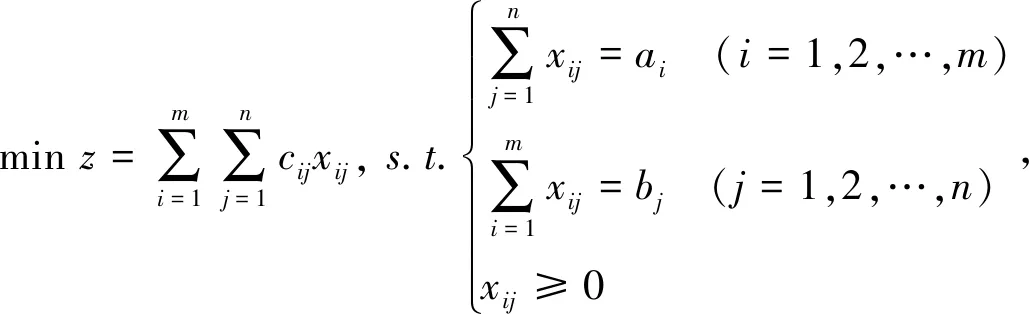
(1)

其中，xij表示从产地i至销售地j的运输量，cij表示从产地i至销售地j的运输单价。

1.2 运输问题的最优性检验

一般运输问题的求解过程也属于线性规划问题，因此其采用的是线性规划问题的基本思想：单纯形法。但由于平衡运输问题系数矩阵的特殊性，对单纯形法进行了一定程度上的简化，即表上作业法[4]，包含的主要过程有[5]：①寻找初始运输方案。寻找初始运输方案即根据实际运输问题找到一个最初的、可行的运输方案，根据单纯形法的思想，即寻找该运输问题的初始可行解。常用的寻找初始运输方案的方法为最小元素法，这里不再赘述。②最优性检验。最优性检验即对上一过程中寻找到的初始运输方案进行检验，判断其是否为该运输问题的最优解。常用的最优性检验方法有闭合回路法和位势法，闭合回路法的思想已有学者进行了研究，即对该方案中无运输量的线路增加运量，如果费用减少，则该方案不是最优方案，反之则为最优方案；位势法在现有的文献中均采用对偶变量的概念进行解释。③运输方案的改进。改进运输方案即根据最优性检验的结果，如果方案为最优方案，则无需改进，如果非最优结果，则需要对方案进行改进，以此类推，直至方案最优。

以上3个步骤中，寻找初始运输方案以及运输方案的改进研究较为成熟，而最优性检验过程中所采用的位势法在现有的文献中均采用对偶变量的概念进行解释，没有类似于闭合回路法中对实际经济意义原理的阐述，造成了学习和理解中的困难。

2 最优性检验位势法的剖析及其经济意义

2.1 运输问题最优性检验的位势法

位势法又称为对偶变量法，根据对偶定理，式(1)的对偶模型可以表示为[6]

(2)

其中，ui和vj为运输问题的对偶变量[7]。

根据线性规划的单纯形法，对上述运输问题进行单纯形法的求解时，非基变量的检验数可以表示为

∂ij=cij-(ui+vj) 。

(3)

由单纯形法的基本思想可知，在求解线性规划问题时，对运输问题中有运量的线路来说，其变量检验数为0，表示为

∂ij=cij-(ui+vj)=0，i,j∈N。

(4)

对于非基变量来说，其检验数表示为

∂ij=cij-(ui+vj)，i,j∈N。

(5)

根据运输问题的模型(1)可知，其目标函数为求最小运费，即求最小值，因而非基变量检验数在取得最优值时应该大于0，即

∂ij=cij-(ui+vj)>0，i,j∈N。

(6)

可以推得

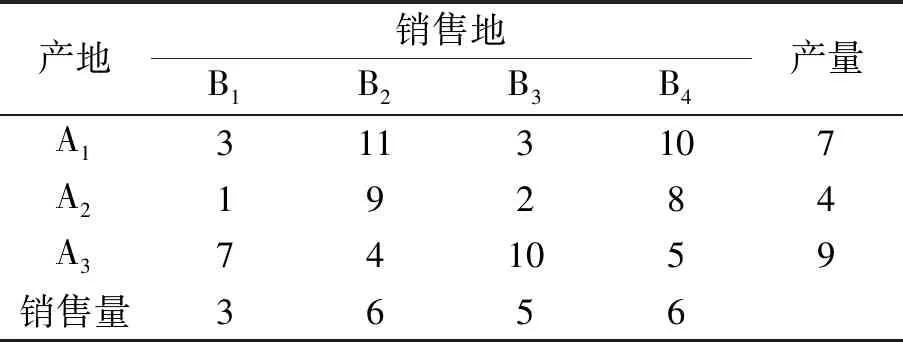
ui+vj

(7)

式(7)的直观解释为，当运输问题取得最优方案时，在没有运量的线路上，对偶变量之和应小于该线路上的运输单价。

2.2 对偶变量的经济意义解释

在运输问题的对偶模型中，ui和vj为运输问题的对偶变量，而在运输问题的表格法中，ui和vj则分别表示产地i和销售地j的“位势”。

“位势”一词最早源于物理学[8]，1687 年牛顿在其巨著《自然哲学的数学原理》一书中的万有引力定律中提出了位势的概念，即位势是一个包含空间概念，随着测度点距离物体的远近而发生变化的物理量；同时位势还受物体本身质量大小的影响，在相同的距离下，质量大的物体其位势高[9]。 在运输问题中，位势可以结合运输问题的主要参数，即“价格”或者“价值”，可以理解为运输货物在不同地点的“价值”。因此，本文将“运输位势”界定为在运输问题中，商品在不同产地或销售地的价值大小。结合前文对“运输位势”的定义，在运输问题对偶模型中，ui和vj即分别表示产地i和销售地j的商品价值。由于在金融界，商品价值可以为负值，因此ui和vj的取值范围是无约束的，这也与运输问题对偶模型式(2)中的约束条件是一致的。

2.3 运输位势基础上的最优性检验原理

前文分析了对偶变量的经济意义，即运输位势。因此，最优性检验的检验数可以理解为利用两地之间的价值之差与运输价格进行比较，现举例说明最优性检验的原理。

在一个由3个产地和4个销售地组成的运输问题中，运输单价见表1。通过最小元素法进行初始方案求解时，可得以下初始方案(表2)，则以位势法进行最优性检验时，各个产地的位势ui和各个销售地的位势vj分别在表格的最后一列和最后一行表示。

表1 运输问题运价表 Tab.1 Tariff of transportation problem

表2 初始方案及位势表 Tab.2 Initial scheme and potential table

以从产地A2到销售地B2线路为例，该线路所对应的非基变量检验数为

∂22=c22-(u2+v2)=9-(-1+9)=1。

(8)

式(8)说明，若厂家选择由A2购买1单位该货物时，所需支出费用为1个单位，运输到销售地B2所需运费为 9个单位，在B2销售地进行销售时，所获得收益为9个单位，因此其运费大于收益，则该线路上没有运输量，即其检验数为正。

由于在运输问题中，非基变量所对应的线路上运输量为0，则若所有非基变量所对应的线路检验数均大于0，则说明这些没有运输量的线路上的运价均大于收益。若在这些线路上增加运量，则收益将会减小，因此，非基变量检验数均大于0的运输方案无需调整，即为最优方案。

3 结论

运输问题最优性检验经济意义的剖析，对于掌握和理解运输问题的具体方法具有极大的促进作用。本文通过对运输问题对偶模型及对偶变量的分析，创新性地提出了“运输位势”的概念，给运输问题对偶变量赋予了实际的经济学含义，对运输问题的教学具有重要的促进意义。