化归思想方法在微积分课程中的应用

王耀卫

(仰恩大学 数学系，福建 泉州 362014)

0 引言

数学思想方法是数学的本质、数学的精髓，是联系数学知识的纽带。学习数学从根本上讲就是获得数学的思想和方法，并用以指导工作和生活。日本数学教育家米山国藏深刻地指出：学生们在校期间接受的数学知识，因毕业进入社会后没有机会应用这种作为知识的数学，然而不管他们从事什么业务工作，唯有深深地铭刻于头脑中的数学的精神,数学的思维方法、研究方法、推理方法和着眼点等，却随时随地发生作用，使他们受益终身[1]。

化归思想方法作为一种重要的数学思想方法被广泛应用。微积分教材就是以化归思想方法为主线将微积分基本理论知识有序编排。这很好地体现了数学知识之间逻辑性强的特点，同时也符合知识发现和问题解决的教学规律，而且有利于培养学生的创新思维能力和逻辑思维能力。本文通过若干事例展现化归思想方法在解决微积分问题中的具体应用，并给出其使用时的一般原则，便于师生学习和掌握。

1 化归思想方法的基本思想

“化归”即转化与归结，其基本思想是：把待解决的问题，通过转化过程，归结为一类已经解决或较易解决的问题，以求得解决[2-3]。转化的手段称为化归的途径，往往借助于其他的数学方法，如换元法、比较法、归纳法、构造法等。化归模式见图1。

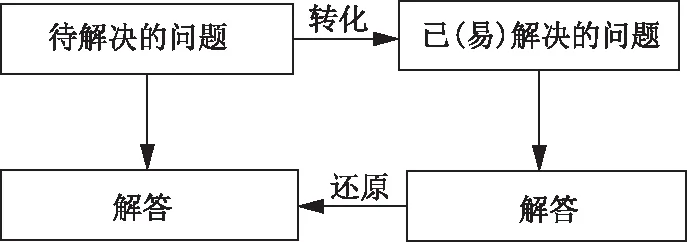
图1 化归模式Fig.1 Reduction Model

2 应用事例

2.1 函数的极限问题

这部分内容以基本初等函数极限情况和极限四则运算法则以及复合函数极限运算法则为基础，其他函数的极限问题则是在化归思想方法的引导下通过具体的方法化为以上情况解决的。

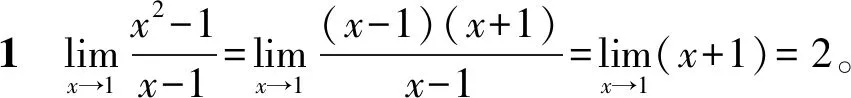
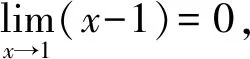
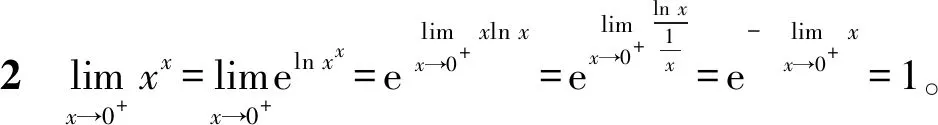
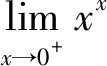
2.2 函数的导数问题

此类问题以一元函数的导数基本公式、导数基本运算法则和一元复合函数导数运算法则为基础，其他情况则以化归思想方法为指导进行转化而求解。

例3[4](隐函数求导问题)方程x2+3xy+y2=1确定y=f(x)，求y′。

通过对方程“两边求导”将其转化为导数的基本问题，再通过求解“关于y′”的方程，得到y′，即，对方程x2+3xy+y2=1两端自变量x求导数，有

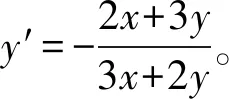
例4(求多元函数偏导数问题)求二元函数z=x3+6x2y-y3的一阶偏导数。

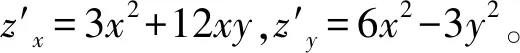
此问题是通过将“二元函数偏导数的定义”转化为一元函数导数问题解决的。

2.3 积分问题

1)一元函数的不定积分问题。这类问题的求解以一元函数的不定积分基本公式和基本运算法则为基础，其他情况则是通过“换元法”“分部积分法”等方法转化为直接积分问题而求解。

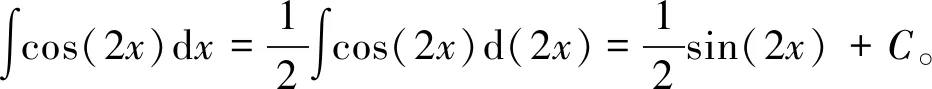
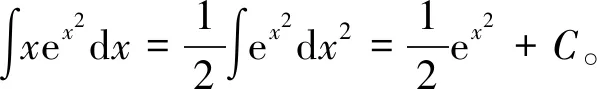
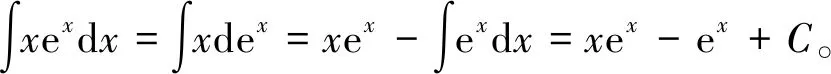
2)直角坐标系下二元函数的积分问题。这类问题通过利用“求平行截面面积为已知的立体体积”的方法将二重积分转化为二次积分，最后只需计算两个一元函数定积分，即

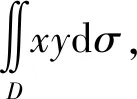
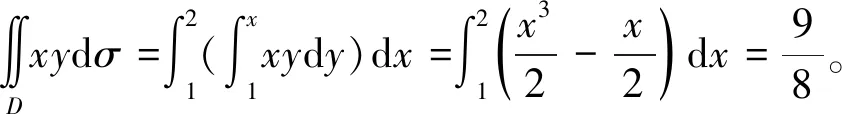
以上只列举了几个主要应用，除此之外还有将函数单调性和极值的判断、最值的求解、曲线凹凸性的判断等问题化归为函数的一阶、二阶导数的问题，将平面图形面积和旋转体体积求解化归为定积分问题，以及无穷积分的求解问题[6]等。

3 化归的基本原则[1]

由于组成数学问题的要素之间相互联系的方式多种多样，化归思想方法仅提供了解决数学问题的目标方向，而在具体应用时没有一个统一的模式，需具体问题具体分析找出“未知”和“已知”之间的化归途径和方法。大量的解题实践表明，为了实施有效化归，遵守一些基本原则是有益的。

3.1 简单化原则

一个数学问题可以看成是由一些数学对象按确定的数学关系合乎逻辑地组合而成的具有某种数学意义的系统或关系结构。对于结构复杂的问题，人们总是力求使之简单化，这即是解题化归遵循的简单化原则。具体来讲就是：在研究解决复杂问题过程中，人们应该考虑变换问题结构，使之变得表现形式上简单或处理方式上简便，通过对这个结构简单的问题的求解，而获得原问题的解决。

3.2 熟悉化原则

一个不易解决的问题朝哪个方向化归，最自然的化归方向莫过于向熟悉的问题、熟悉的方法化归了，此即熟悉化原则。这就要求对学过的数学知识和数学方法要尽可能地熟练掌握。

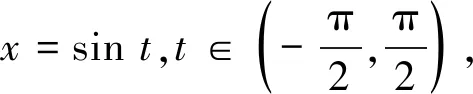
3.3 标准化形式原则

化归的标准化形式原则是说将待解决的问题在形式上向该类问题的标准形式化归。标准形式是指已经建立起来的典型的、规范的数学模式。

3.4 低层次化原则

化归的低层次化原则是说解决数学问题时应尽量将高维空间待解问题化归成低维空间的问题，高次数的问题化归成低次数的问题，多元问题化归成少元问题解决。比如：二元函数偏导数的问题化归成一元函数的导数问题，二重积分的问题化归成一元函数积分问题等。

4 结语

可以说，化归思想方法始终贯穿于微积分教材，始终贯穿于微积分问题的整个解题过程[9]。授人以鱼，不如授人以渔。在教学过程中，教师的任务不仅在于讲授数学知识，更重要的是要介绍和传授数学思想方法。教师及时启发学生使用这些思想方法将有助于培养学生的独立思考能力和自主学习能力。