高中数学核心素养背景下问题导学课堂教学研究

赖国强

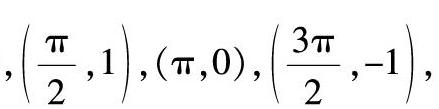
[摘  要] 核心素养以及数学学科核心素养是一个具有包容性的概念，它应当能够兼容高中数学教学的优秀传统，相应的在高中数学教学中积累下来的优秀教学思路以及策略，也应当成为数学学科核心素养培育的重要途径. 如果采用问题导学的方式，让学生在对问题或者系列问题进行思考的过程当中，逐步走入数学学习的情境，那学生的学习效率就会大增，而且学习能力会切实得到培养，核心素养也会更加顺利地落地. 当教师带着这样的意识与目标去设计教学的时候，核心素养的培育与问题导学才能有机地融为一体，两者之间也才能发挥相互促进的作用.

[关键词] 高中数学;课堂教学;核心素养;问题导学

在最新版《普通高中数学课程标准》正式颁布之后，数学学科核心素养的培育也就成为高中数学教学的当务之急. 因此，核心素养“落地”就成为当下教育领域研究的重点和热点，从数学学科出发，数学核心素养落实问题更是引发了数学教育界的普遍关注. 有一点需要注意的是，尽管数学学科核心素养的培育，已经成为当下高中数学教学的重要目标，但是这并不意味着要摒弃已有的传统，而将所有的教学注意力全部转到核心素养培养当中来. 数学教师应当认识到，核心素养以及数学学科核心素养是一个具有包容性的概念，它应当能够兼容高中数学教学的优秀传统，相应的在高中数学教学中积累下来的优秀教学思路以及策略，也应当成为数学学科核心素养培育的重要途径. 在这样的思路之下，笔者对高中数学核心素养背景下的“问题导学”及其课堂教学进行了深入的研究，获得了许多有价值的认识. 在此将这些认识总结出来，希望能够给当下的高中数学教学起到抛砖引玉的作用.

■用高中数学核心素养引领问题导学课堂教学

问题导学是高中数学教学研究当中积累下来的一个非常有价值的教学思路，在问题导学这一教学理念诞生之初，人们认识到传统的讲授式甚至是灌输式的教学，只能让学生机械地积累相关的数学知识，并不能让学生的数学学习能力以及问题解决能力得到培养. 相反，如果采用问题导学的方式，让学生在对问题或者系列问题进行思考的过程当中，逐步走入数学学习的情境，那学生的学习效率就会大增，而且学习能力也会切实得到培养. 很显然这样的教学结果，与当下核心素养的追求是一致的. 因此基于这些宏观分析可以得出的一个基本结论是：课堂教学要融入学科核心素养的培养，而相应的“问题导学”教学思路也为落实数学核心素养的培养提供了理论依据和操作方法. 具体有两点理解：一是用高中数学核心素养来引领问题导学课堂教学，可以让问题导学更加具有针对性;二是打造问题导学的课堂教学，可以让数学学科核心素养更好地落地.

具体来说，问题在高中数学教学中的重要性不言而喻，可是在教学当中为什么要设计问题？这个问题却不那么容易回答. 比较好的理解是：站在学生的角度思考学生的学习过程，可以发现在高中数学学习的过程当中，数学知识的积累以及数学能力的养成都是依靠思维而发生的，在学习的过程当中思维要想活跃起来，最好的撬动方式就是问题. 而在核心素养的背景之下回答这一问题，则可以认为为了核心素养培育的需要，为了让数学学科核心素养的相关要素能够落地，可以通过问题来打开学生数学抽象、逻辑推理或者数学建模的空间. 于是对问题导学的理解就可以进一步拓宽：问题所导的不只是教學过程，还有教学目标的实现.

对于教师而言，认识到问题导学的价值，其实还是提醒教师要站在学生的角度去思考问题：学习是学生自己的事情，教师所设计出来的问题，是为了引导学生的学习的. 如果问题设计得当，如果所设计出来的问题在最好的时机提出，那问题就能够真正起到导学的作用，学生的学习过程也就自然会顺利，那数学知识教学的目标以及核心素养培育的目标就能够顺利落地.

■问题导学课堂教学中高中数学核心素养培育

通过上面的分析可以发现，在核心素养的背景之下研究问题导学，实际上是问题导学这一教学方式，与核心素养这一教学目标相辅相成的关系研究. 对核心素养的理解可以是：在高中数学教学中，教师应当聚焦学生的数学核心素养，数学教学应当从“知识取向”转向“素养取向”. 具体到教学中，教师需要以“问题”为载体，建构“问题导学”课堂，串联起学生主体、教师主导、探究过程、知识获得、能力提升等诸多要素，从而让学生经历一个由“渔”获“鱼”的学习历程. 下面以“三角函数的图像与性质”这一内容的教学为例来说明.

“三角函数的图像与性质”这一内容的教学，从正弦函数和余弦函数的图像学习切入，然后在图像研究的过程当中得到正弦函数和余弦函数的性质. 很显然，“三角函数的图像”是“三角函数的性质”学习的基础. 在学习正弦函数和余弦函数的图像的时候，教师可以先引导学生复习“实数集”与“角的集合”之间一一对应的关系，让学生认识到一个确定的角就能对应一个确定的正弦或者余弦值. 于是给定一个实数x，就有唯一确定的sinx或cosx与之对应. 有了这种对应关系之后，就可以顺利建立起正弦函数和余弦函数的概念理解，并且可以顺利确定两者的定义域.

根据前面所学的知识，教师可以首先提出一个宏观性的问题：根据此前所学函数的模式，在学习正弦函数和余弦函数的时候，你觉得需要学习哪些内容？

事实证明这个问题可以撬动学生系统回忆所学过的函数知识，如果教师有效地组织学生进行自主思考与小组合作，那学生就能认识到学习一个新的函数，首先就要画出它的图像，然后去观察这些图像的特点，就是借助于图像去研究函数的性质. 学生通过更加深入的思考与组织，可以认识到学习函数的性质就是从值域、单调性、奇偶性、最大值、最小值等角度去学习.

分析上述这个问题的提出以及学生的思考结果，可以发现一个问题确实可以调动学生的已有认知，可以让学生在一定逻辑的基础之上去梳理函数学习与性质理解之间的关系. 当学生得出上述认识之后，对正弦函数和余弦函数图像及其性质的学习，也就有了一个大致的思路，这个思路可以引导学生自主思考、自主探究，从而获得新的知识认识，并在此过程中体验数学学科核心素养的相关要素. 比如说，在学生作出正弦函数的图像之后，教师可以提出一个问题：结合你所作出的正弦函数图像过程，你觉得要准确地作出正弦函数的图像，应当关注哪些关键点？

这个问题必然可以让学生去进一步回顾正弦函数图像的作出过程，而凭着绝大多数高中学生正常的思维能力，他们也能认识到起关键作用的点就是5个，分别是（0，0），■，1，（π，0），■，-1，（2π，0）. 实际上，相当一部分学生都能有这一发现，有了这一发现再去作函数图像，甚至是生成正弦函数的性质，就会变得轻车熟路.

■核心素养背景下问题导学课堂教学研究反思

在上面的实践当中，好多认识与结论都是学生自主得出的，即使对于一些重要的结论，学生可能最初得出的认识比较模糊，描述出来还比较粗糙，但是在教师引导之后，他们也大多能够准确理解用数学语言描述的三角函数的性质. 这说明学生的学习过程是有效的，学生在这些过程当中也建立了有效的逻辑推理及数学建模的过程，因此数学学科核心素养的培育，也能得到强有力的保障.

由此来反思核心素养背景下高中数学课堂上的问题导学，再去解决核心素养的概念时，就会发现“核心素养”是指学生适应终身发展和社会发展需要的必备品格和关键能力，而这正是培养学生的核心素养是教师教学任务的重要理念之一. 再思考问题导学及其与核心素养之间的关系，也会有新的发现，比如说作为数学教师，在教学设计的时候要思考所设计出的问题能否有效地实现导学的目标，能否有效地将数学学科核心素养的不同要素渗透到学生的学习过程当中去. 可以肯定地讲，只有当教师带着这样的意识与目标去设计教学的时候，核心素养的培育与问题导学才能有机地融为一体，两者之间也才能发挥相互促进的作用.

综上所述，核心素养背景下的高中数学问题导学是一个有价值的研究课题，教师一方面要进行充分的理论吸收，另一方面要积极进行实践. 只有将理论与实践结合起来，核心素养背景下的问题导学才能更为充分地发挥应有的价值.