抓住思维资源，拓展引导教学

陶金龙

[摘  要] 学习的过程即思维不断完善和发展的过程，教师要善于抓住思维资源，寻找开拓思维的新“契机”，运用灵活多样的教学手段进行引导，从而使课堂更加丰富多彩。

[关键词] 思维资源;开拓;精彩

思维因受教学方式、教学环境、个体认知等诸多因素的影响，既存在其共性，又有其差异性，因此，教学中应尊重差异，给学生提供足够的时间和空间，让学生获得丰富的思维体验，从而收获意想不到的精彩。思维资源的重要性是不言而喻的，那么教学中如何引导，才能发挥其重要作用呢？笔者通过以下几点进行说明。

■一、思维出彩时，灵活性引导激发思维

每个学生都是独立的个体，都有其独特的见解和鲜活的想法，教师要善于发现学生的闪光点，并给其充分地肯定、尊重和鼓励，只有这样才能让学生敢于表达真实的、独特的想法，为思维拓展提供生长的平台。

案例1  长方形变正方形

师：今天遇到了这样一个问题，学校原来有一个用砖砌的长8米，宽6米的花坛，现在学校想将其改造为正方形花坛，为了节约成本，高度不变，使用原来的砌墙砖，你们说这能办到吗？

生1：应该可以的，高度不变，我们就只需要考虑周长。

师：非常好，那么现在大家分组讨论一下该如何改建吧。（问题给出后学生很快给出答案）

生2：老师，我们组认为：根据已知，长方形的长为8米，宽为6米，那么可求出长方形周长为28米，因此，正方形的边长为28÷4=7（米）。

师：很好的办法，利用我们已学的周长知识解决了这个实际问题。那么还有其他的办法吗？

生3：我们组没有求周长，就直接用8+6=14（米），14÷2=7（米）。（有些同学表示不解）

生3：就是相当于分段，长和宽相加等于2段的长度，那么除以2，就可以了。（经过讲解都表示理解了）

生4：老师我是这样想的，已知长为8米，宽为6米，也就是长比宽多了2米，那么把多的分一分就可以了。（大家纷纷鼓掌，有学生说，我们在家分糖就这样分的。）

一个简单的案例，学生就给出了多种方案，因此，在教学中教师要留给学生足够的时间和空间，让学生放手去“做”，这样可以使学生思维大放异彩。如果在生2给出答案后，就结束了本题的探究，怎么会知道原来学生可以想出更多的可操作性方法呢？怎么能收获一个自由、轻松、和谐的课堂呢？因此，在教学中，教师要学会放手，让学生多想、多动，从而获得更多解决问题的方法，拓展学生思维能力。

■二、思维肤浅时，发散性引导深化思维

教学不仅仅是简单的传授，更多的是用激励和引导唤醒沉睡的思维。当学生的思维无法深入时，要适当地用问题进行激一激，让学生可以顺着问题深入思考，从而使学生思维更有深度也更成熟。

案例2  乘法的应用

师：生活中到处用到乘法，现在我们就以教室为例，看看你们能找出哪些乘法。

生1：教室的玻璃。教室一共有9扇玻璃，每扇有两块大的一块小的，那么大的有2×9=18（块），小的有9×1=9（块），合起来是3×9=27（块）。

师：很好的应用，还有哪些呢？

生2：我们教室的桌子，一共有6排，每排有8张，但是最后一排少了一张，只有7张。

师：那你算出的结果是？

生2：我是用6×8-1=47。

师：那么你是怎么想的呢？（教师进一步提问，以让其他学生了解解题思路）

生2：因为最后缺了一个，那么可以先借用一个补上，后面再减去就可以了。

生3：可以直接用5×8+7=47。（学生迫不及待地回答）

生4：也可以用7×6+5=47。（有些学生表示不解）

师：说说你的想法。

生4：我是纵向看的，一共有8列，每列6张，但是第8列少一个，所以我考虑7列，然后加上第8列的5。（学生用手比画着，害怕其他学生不能理解）

教学中，教师采用了大家看得到的场景进行乘法应用的展开，使学生更直观地感受乘法应用的意义，发散性问题的引导让学生逐层思考，使思维走向更深处。

■三、思维迷糊时，辅导性引导梳理思维

教学的展开应建立在已学知识或已有经验的基础之上，但有些题目往往忽略差异，使学生无法理解题意，造成思维模糊。出现这种情况时，教师要及时地进行辅导性引导，将其转化为已有的认知或经验。

例如，教学中遇到这样的题目：小强要参加100米的自由泳比赛，已知他来回了两次，请问泳道长为多少？

题目给出后，很多学生对泳道没有概念，对来回理解不清，所以无法读懂题意，做题显得无从下手。

教师这样进行引导：

①我们学校有50米的直线跑道，那么来回一次是多少米呢？

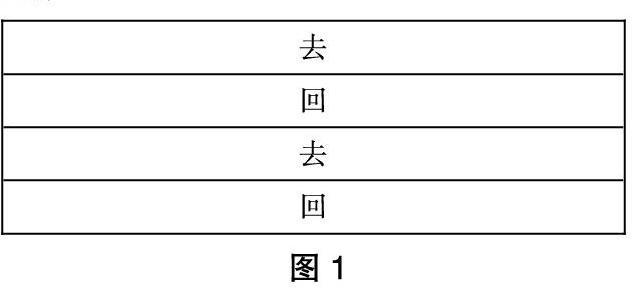
②如图1，教师用图形展示来回的过程。

图1

通过教师的引导，将其转化为已有的认知和生活经验，又将题目用图形进行直观的展示，符合低年级学生的认知，让学生轻松地理解了题意，解题变得水到渠成了。

在教学中，教师要清晰地了解学生的现状，通过题目的变形或图形对模糊的思维进行及时的梳理，以防止学生因不解题意而在模糊的意识里消耗精力，影响学习士气。

■四、思维中断时，联系性引导打开思维

在遇到一些抽象的问题或者新问题时，经常会让学生感觉不知所措，无从下手，思维发展中断。那么遇到这种情况教师应如何解决呢？

案例3  豎式计算

师：下面请同学们用竖式计算48÷2。（题目给出后，学生都轻松给出了竖式）

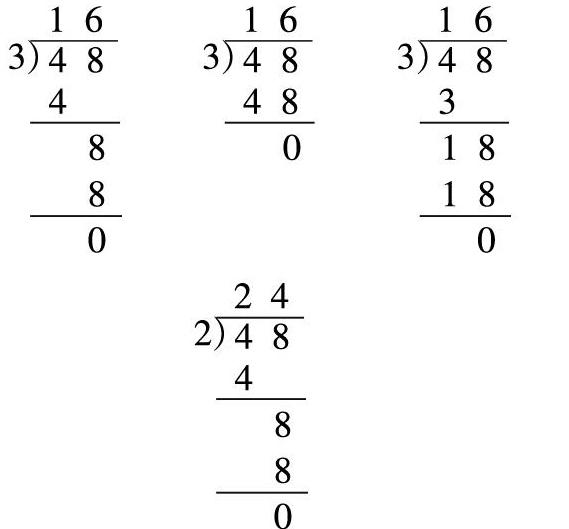
师：很好，下面请同学们继续计算48÷3。（经过汇总，共有3种写法，教师板书进行展示）

师：你们认为哪个才是对的呢？

师：现在请大家用学具盒里的小棒重现一下你们分组的过程，看看有什么发现？（学生拿出了4捆小棒，每捆10个，另外又拿出单独的8根）

生1：我是这样分的，因为是除以3，那么就分成3份，4捆可以一份先分1捆，然后还有1捆不够3人分，就将其拆开，与单独的8根放在一起是18根，18根再分成3份，每份再得到6根，这样每份就是16根。

师：很好，大家有不同的分法吗？（大家表示都赞同这样的分法）

师：那么哪个竖式体现了这一过程呢？

经过联系实际的引导，利用学生平分的经验，使学生找到了正确的竖式。无论学优生还是学困生，在遇到抽象的问题时都可能产生困惑，这时，教师可以通过已学知识或现实情境进行解惑，抑或教师可以以例题方式进行展示，直接给出标准步骤，让学生根据步骤再现刚刚的现实情境，强化思维，使之找到突破口，从而使学习更加顺畅。

■五、思维犯错时，启发性引导清理思维

错误是再学习的礼物，里面包裹着疑惑、困难、习惯，映射出学习状态和学习风貌。因此，错误是宝贵的学习资源，要善于收集、整理、汇总、反思，使之成为完善思维的有意武器。

案例4  分数混合运算

师：已知第一天直播的成交额为39万元，第二天的成交额比第一天多■，请问第二天的成交额是多少？（学生直接给出了答案）

生1：39+39÷■。（有些反应快的学生已经发现了错误）

师：好的，那你说一下你的思路。

生1：用第一天的成交额加上增加的■。

师：那39÷■代表何意义呢？

生1：第一天是39万元，第二天增加了它的■。哦，错了，不是除是乘，39×■。

生2：其实可以直接用39÷3。（学生补充道）

师：说说你的想法。

生2：把39平均分成3分。增加了其中的一份，即39÷3。

生3：那根据这个理解，也可以用39÷3×4。（很多学生有些疑惑了）

师：那你说说你的想法。

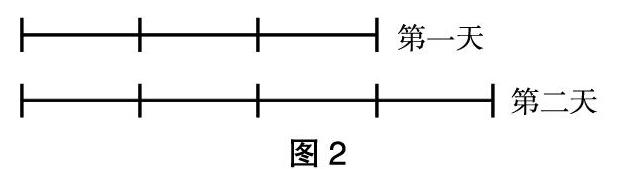
生3：我是根据以前的线段法进行解题的，如图2，如果把第一天看成“1”，将其平均分为3份，即每份为39÷3，第二天的成交额为4份。（通过图形和讲解后大家都理解了这个解法）

利用学生的错误，使学生更加深刻地理解了39÷■与39×■的真实内含。根据学生份数的提出，顺着学生思维的发展，让学生通过线段图理解了第二种解法。以错误为起点，沿着学生的思路，通过交流、引导，使学生获得了更多的数学体验。这样顺势而为，既照顾了学生的思路和积极性，又帮助学生理清了错误思维，第二种方案的给出，让学生收获了意外的精彩。

总之，学生思维的成长是一點一滴积累的过程，教师要抓住各种思维资源，合理的利用和引导，使之不断开拓和完善，最终形成自己特有的知识体系。