借魔术东风 育模型思想
郑烨婷
[摘 要] 《义务教育数学课程标准(2011年版)》提出了适应学生发展和提高数学素养的十个核心概念,“模型思想”是新增的核心概念之一,史宁中教授更是把“模型思想”列为小学阶段三大数学基本思想之一,但是相比其他核心概念,“模型思想”比较抽象。数学魔术的表演和破解需要学生经历“从实际生活中提取数学模型—求解数学模型—应用数学模型”的过程,它是培养学生“模型思想”的良好载体。
[关键词] 数学魔术;数学模型;模型思想
■一、背景介绍
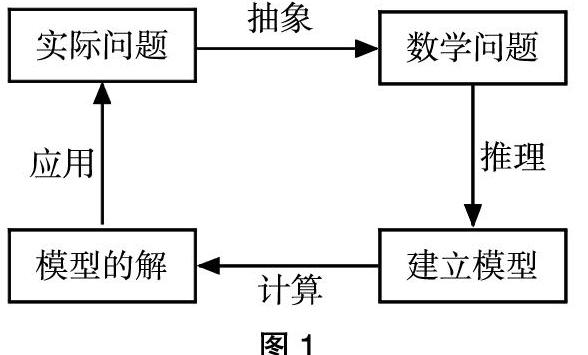
《义务教育数学课程标准(2011年版)》提出了十大核心概念,“模型思想”是新增的核心概念之一,并指出:“模型思想的建立是学生体会和理解数学与外部世界联系的基本途径,建立和求解模型的过程包括:从现实生活或具体情境中抽象出数学问题,用数学符号建立方程、不等式、函数等表示数学问题中的数量关系和变化规律,求出结果并讨论结果的意义。”该论述明确了义务教育阶段模型思想的价值和建立模型的基本过程(如图1):
相比其他核心概念,模型思想比较抽象,一线教师常常对此束手无策。在教学实践中笔者发现,数学魔术是培养学生模型思想的良好载体。通过数学魔术的表演,引导学生用数学的眼光去观察、分析和表示魔术中的各种变量,抽象出数学模型;在数学魔术背后的数学原理探究中,通过猜想、计算、推理、验证等一系列的思维过程,求出模型的解,从而解释魔术现象。数学魔术的过程旨在培养学生建立数学模型、解决实际问题的意识与能力。
本文将以数学魔术“猜一猜:硬币在哪儿”为例,介绍如何借助数学魔术的教学,培养学生的模型思想。
■二、教学实践
1. 魔术引入:感受神奇,激发兴趣
精彩的课堂导入能迅速激发学生的学习欲望,有效唤起学生的课堂注意。数学课堂导入的方法有很多,用魔术进行课堂导入可以增添问题的神秘感,通过生动有趣的表演让平时看起来不可能的事情现在就发生在眼前,孩子们的好奇心一下子会被激发出来。这时,“太神奇了吧”“是真的吗”“老师是怎么做到的”等惊讶问题就会自然而然地萦绕在学生的脑海里,欲“解”不达,欲罢不能。通过以数学魔术导入引发思考探究的活动,能有效激发学生的思维活力,使学生把精力集中在思考和探究数学问题上,从而取得更为理想的学习效果。
生活中经常会玩这样的游戏:把一个小物品藏在某一只手中,让对方猜一猜藏在哪只手里。基于这样的灵感,设计了以下的魔术:
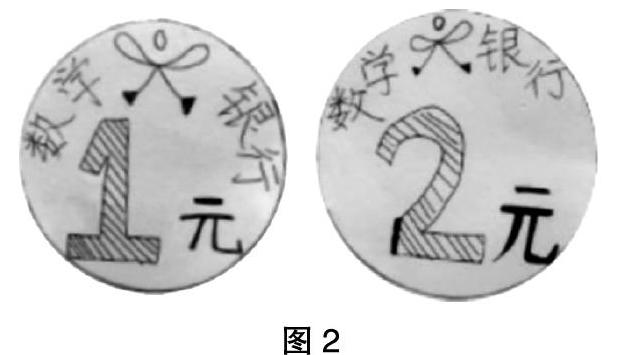
师:(出示两个硬币,如图2)今天老师要用数学银行自制的1元、2元硬币来玩一个魔术。看过魔术表演吗?
生:看过。(兴奋的表情露在脸上)
师:老师要变的魔术叫“读心术”,等会儿老师请一个助手上来,请他把这两枚硬币分别藏在左右两只手上,我不用看就知道这两枚硬币分别藏在哪只手上。誰愿意来做老师的助手?
指名上台和教师合作。
师:(对助手)来,先请你看看这里的两枚硬币,一枚是1元,一枚是2元,有没有问题?(没有)好!下面请你将它们打乱,然后将它们分别藏在左右两只手里。老师不用看,只要他回答我一个问题,我就能知道这两枚硬币分别藏在哪只手上。相信吗?
学生中有信的,也有不信的。
师:请你把左手里的钱数加两次,右手里的钱数加三次,再把得出的两个数相加(边说边板书:左+左+右+右+右),嘘……请告诉我结果是奇数还是偶数。
生:是偶数。
师:那么,1元硬币藏在左手边,2元硬币藏在右手边。
助理揭开答案,学生纷纷赞叹不已。
数学模型的建立首先要“从现实生活或具体情境中抽象出数学问题”,说明情境是建模的源点,也就是魔术的表演是这节课建模的源点,从中抽象出数学问题是建模的起点,从魔术表演到问题的环节可称为“建模准备”。
2. 魔术分析:思考关系,尝试建模
数学建模的关键是用数学符号建立方程、不等式、函数等表示数学问题中的数量关系和变化规律,学生要通过观察、分析、抽象、判断、推理等数学活动将数学魔术问题抽象、简化,建立数学问题中的数量关系。在“猜一猜:硬币在哪儿”这个数学魔术中,左手里硬币的钱数加两次,右手里硬币的钱数加三次,最后合起来的结果是奇数还是偶数是关键,因此要引导学生思考和的奇偶性与加数有什么关系,建立和的奇偶性这一数学模型。
师:你们有什么疑问吗?
生:老师,你会不会是蒙对的?(如果学生发出这样的疑问,可以再进行一次表演)
生:老师,你会不会跟助理串通好了?
生:老师,你有超人的能力。
师:你们觉得老师到底是有超人的能力,还是有好方法呢?
生:我觉得老师是有方法的。
师:对啊,魔术都是有窍门的。那么,你们觉得这个魔术的关键在哪里?
生:在老师提出的那个问题。
生:左手里硬币的钱数加两次,右手里硬币的钱数加三次,最后合起来是偶数。
师:同学们太厉害了!这么快就发现了魔术中的秘密,老师就是根据和是奇数还是偶数倒推出来的。几个数相加,和是奇数还是偶数这样的问题被称为“和的奇偶性”。要想研究和的奇偶性,解决类似的问题,你打算怎么研究?
生:左+左+右+右+右,5个数相加太多了,可以从两个数的和开始研究。
师:研究两个数的和的奇偶性,你有什么方法?
生:可以通过举例发现。
3. 魔术探究:发现规律,稳定模型
数学魔术不仅要让学生感受到好玩、有趣,更要让学生通过猜想、启发、验证、推理、创造等一系列的思维过程探究魔术背后的数学原理,以及在这个过程中积累数学活动经验、感悟数学思想和方法。
学生通过举例得出:
发现:奇数+奇数=偶数,偶数+偶数=偶数,奇数+偶数=奇数。从例子中发现规律还不够,教师还要让五年级的学生感受到数学是一门严谨的学科,引导学生从余数的知识、画图等方法来进行验证。得到两个数的和的奇偶性后,学生就可以顺势推导出多个加数的和的奇偶性了。教师借势引导小结:
师:所以,你们认为和的奇偶性与加数中谁的个数有关系呢?
生:与加数中奇数的个数有关系,奇数个奇数相加,和就是奇数;偶数个奇数相加,和就是偶数。
模型的求解常常需要借助一定的方法策略,如举例、数形结合、假设、推理等,有效的方法和策略为学生进一步建模、解决问题提供帮助,提升解决问题的效率。通过举例发现规律只是猜想,要引导学生通过严谨的证明来验证猜想是对的,数与形的结合是小学数学中解决问题常用的方法,解决问题时常常需要借助图形直观分析问题,猜想得到的和的奇偶性的规律后借助图形的直观,得到验证。
4. 破解魔术:探究原理,应用模型
揭秘是学生欣赏魔术表演后最想做的事。教学中要有效地引导学生探究魔术的设计原理,利用已经得出的数学模型来解释魔术现象,完整地经历建模过程,充分感受模型思想。
师:同学们,现在你们能说说老师是如何快速得出1元硬币藏在左手里,2元硬币藏在右手里的吗?
生:根据助理的回答可以知道“左+左+右+右+右”的结果是偶数,说明奇数1加了偶数次,1元硬币加了两次,所以左手里藏的是1元硬幣。
师:那左右两边加的次数有要求吗?
生:有,一边加奇数次,一边加偶数次。如果两边都加偶数次,结果一定是偶数,就判断不出来了;如果两边都加奇数次,结果一定是奇数,也判断不出来。
师:请同学们进一步思考,硬币的币值可以是任意数吗?
生:必须一个是奇数、一个是偶数,如果硬币币值都是偶数的话,不管加几次结果都是偶数,如果都是奇数也不能成功。
师:老师的神奇魔力就在这儿,事先要设计好魔术的道具和操作的规矩,最后的结果就都在掌控之中了。通过今天的学习,你有什么收获?
生:魔术背后是有数学道理的,弄清数学道理就可以破解魔术了。
生:如果能找到规律,变魔术就很简单了。
生:我也想当一名魔术师。
……
师:知道了魔术的设计原理,我们可以自己尝试设计和破解更多的数学魔术。
■三、教学思考
曹培英老师认为:建模与问题解决的能力是数学最具学科特征的育人价值。数学魔术能带给学生神奇、愉悦的体验,数学魔术的原理又天然具有数学的模型结构。数学魔术的表演和揭秘的过程可以让学生在获取数学知识和技能的过程中体验从实际问题抽象出数学问题,建立数学模型,再通过数学原理得到数学模型的解,从而揭示魔术现象。这一过程有助学生初步形成模型思想,体会到数学建模中用数学方法解决实际问题的好处,也有助教师在现实中探寻培养策略,从而促进学生数学模型思想的形成和发展,最终提高学生的数学素养。

