溶液混合问题“反比关系”的分析与教学研究

郑煜芬 卢建川

[摘  要] 文章通过揭示两种不同浓度的溶液混合后浓度改变的实质，分析“混配的原溶液的质量比等于两原溶液与目标溶液的浓度差的绝对值的反比”的原因;对于浓度混合问题的教学，笔者通过设置系列直观性问题，为学生理解溶液混合问题做铺垫，利用溶质、溶剂分离图，直观表征，迁移应用，突破难点，促进学生对溶液混合问题的直观认识，达到知悉算法、理解算理的教学目标。

[关键词] 溶液混合;濃度差;直观化;难点分化

小学数学六年级百分数应用题教学课题中，两种不同浓度溶液的混合问题是一个教学难点问题。如：现有浓度为10%的糖水20克，再加入多少克浓度为30%的糖水，可以得到浓度为22%的糖水？

不少教师在讲解此类问题时，先使用代数法解决，将问题一般化：设浓度为a%的糖水x克，再加入y克浓度为b%的糖水，可以得到浓度为c%的糖水（假设b>a）。列出如下方程并化简：a%·x+b%·y=c%·（x+y）？（c%-a%）·x=（b%-c%）·y？x∶y=（b%-c%）∶（c%-a%）。

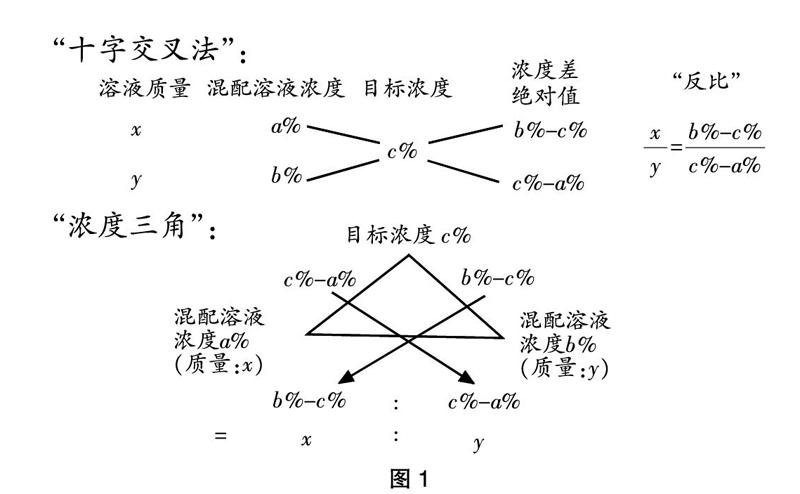
由此直接提炼出“混配的原溶液的质量比等于两原溶液与目标溶液的浓度差的绝对值的反比”这一结论，并将其固化为一个数学计算技巧“十字交叉法”或者“浓度三角”，从而根据这一工具运用算术法解题，如图1。

如此教学，学生并不明白“反比”的道理所在，死记硬背比例公式和解题技巧，不知所以然地套模式解题。

混配溶液问题算术法的难点在于对“混配的原溶液的质量比等于两原溶液与目标溶液的浓度差的绝对值的反比”这一结论的理解。本文通过分离溶质与溶剂，直观地分析浓度变化的实质，阐述“反比”的原因，并设置系列直观问题突破教学难点。

■一、两种不同浓度的溶液混合后浓度改变的实质

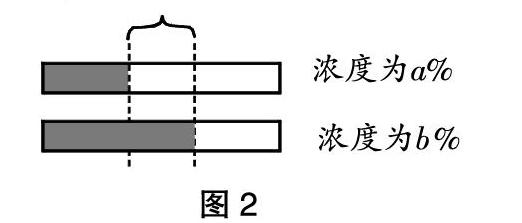
先看溶液质量不变情况下浓度变化的表现与理解。要升高某一溶液的浓度，则根据浓度的计算公式，溶质在溶液中的占比要提高，为了不改变溶液的质量，则要将溶液中的部分溶剂替换为溶质。如图2，要将浓度为a%的溶液的浓度升高为b%，则需要将[（b%-a%）×溶液质量]的溶剂替换为溶质，即将图2中大括号标记的溶剂替换为溶质。对于降低溶液的浓度也可类似地进行讨论，不同的是要将其中的部分溶质替换为溶剂。（图示用长柱表示溶液，其中白色表示溶剂，灰色表示溶质）

再来说两种不同浓度的溶液混合。根据生活经验，一杯很甜的糖水与一杯很淡的糖水混合后，新的糖水就没那么甜也没那么淡。其实这反映了不同浓度的溶液的混合问题，即高浓度的溶液与低浓度的溶液混合后，新溶液的浓度势必介于这两个浓度之间。

为什么会发生浓度的改变呢？其实在于两种不同浓度的溶液混合后，高浓度的溶液提供了一定量的溶质给低浓度的溶液，而低浓度的溶液则提供了等量的溶剂给高浓度的溶液，即高浓度溶液的部分溶质与低浓度溶液的部分溶剂等量交换了。

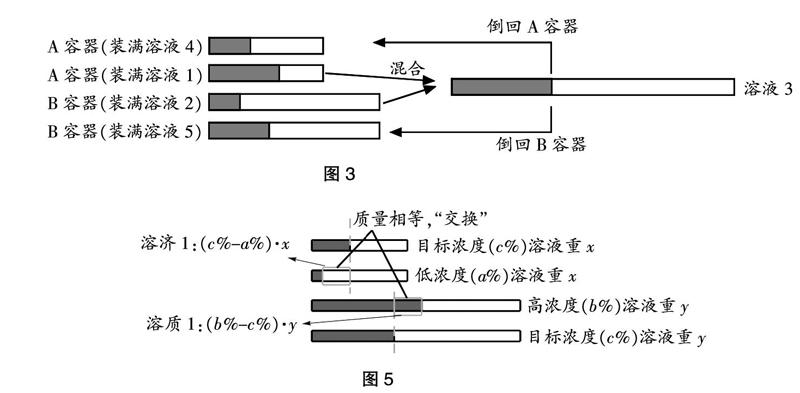
取A、B两个容器，A容器装满高浓度溶液（记为溶液1）、B容器装满低浓度溶液（记为溶液2），将两种溶液混合（记为溶液3），则溶液3中的溶质为溶液1和溶液2的溶质和，溶剂为溶液1和溶液2的溶剂和。由于溶液的浓度与溶液的质量无关，将混合后的溶液倒回A容器（记为溶液4）、B容器（记为溶液5），则溶液4、溶液5与溶液3的浓度是相同的，如图3所示。

将A容器原来的溶液1与现在的溶液4作对比，B容器原来的溶液2与现在的溶液5作对比，则溶液4比溶液1多了溶剂（少了溶质），溶液5比溶液2多了溶质（少了溶剂）。造成这种差别的原因在于溶液1和溶液2混合后，溶液1提供了部分溶质给溶液2，溶液2提供了等量的溶剂给溶液1，即溶液1的部分溶质与溶液2等量的溶剂“交换”了，以达到彼此之间溶质质量与溶液质量的比值相等，即溶液1的浓度降低了，溶液2的浓度升高了，最终等于混合后溶液3的浓度，如图4所示。在这过程中，实质上是运用“关系映射反演”原理，将两溶液混合后浓度改变的问题“化归”为一种溶液浓度改变的问题：溶液1的浓度改变为溶液4的浓度，溶液2的浓度改变为溶液5的浓度，而溶液4、溶液5与溶液3的浓度是相同的，混合后溶液的浓度自然为溶液3的浓度。

所以，两种不同浓度的溶液混合后浓度发生了改变，实质在于高浓度的溶液提取了部分溶质与低浓度的溶液“交换”了溶剂，以达到彼此的浓度相等。在此过程中，高浓度的溶液换部分溶质为溶剂，浓度降低了;低浓度的溶液换等量的溶剂为溶质，浓度升高了，最终达到两者的浓度相等。因此，两种不同浓度的溶液混合后，混合溶液的浓度一定介于两个混配的溶液的浓度之间。

■二、“反比关系”的分析

要将两种不同浓度的溶液配制成一定浓度（介于原来两个浓度之间）的溶液，则“混配的原溶液的质量比等于两原溶液与目标溶液的浓度差的绝对值的反比”，这一结论的直观道理在哪儿？

为了方便表达，设低浓度的溶液浓度为a%，高浓度的溶液浓度为b%，要配置为目标溶液浓度为c%，对应的质量为x的低浓度溶液与质量为y的高浓度溶液，则混合后溶液的质量为x+y。

将混合后溶液再分为质量x与质量y的两份溶液，则这两份溶液的浓度都为c%。根据上述分析，可以将问题“化归”为质量为x的a%溶液改变为质量为x的c%溶液，质量为y的b%溶液改变为质量为y的c%溶液。

a%溶液的浓度要上升为c%，需要将（c%-a%）·x的溶剂（记为溶剂1）换为溶质;b%溶液的浓度要降低为c%，需要将（b%-c%）·y的溶质（记为溶质1）换为溶剂，如图5。

所以，要使a%溶液与b%溶液混合后浓度刚好为c%，则溶剂1需等于溶质1，混合后a%溶液提供溶剂1与b%溶液交换溶质1，使得两者的浓度都变为c%，混合溶液自然也为c%，这也是代数法最后两步的本质所在。

因此，只要低浓度溶液的质量与高浓度溶液的质量的比值等于“高浓度-目标浓度”与“目标浓度-低浓度”的比值，混合后两种浓度的溶液就能各取所需，使得最终浓度刚好为目标浓度。这就是结论“混配的原溶液的质量比等于两原溶液与目标溶液的浓度差的绝对值的反比”。教师在教学过程中应该带领学生看清结论的缘由，这样学生才能知其然并知其所以然，在解题过程才能抓住本质，各种变式题目都万变不离其宗。

■三、基于分化难点的直观化教学方案

对于浓度混合问题，使用算术法解题难度较大，小学生不容易理解，在教学过程中教师应将难点分化，为学生搭建解决问题的阶梯。学生要充分理解浓度混合问题，需掌握以下几点：

（1）两溶液混合后，高浓度溶液为低浓度溶液提供溶质，低浓度溶液为高浓度溶液提供溶剂，以达到彼此的浓度相等;

（2）混配的原溶液的质量比等于两原溶液与目标溶液的浓度差的绝对值的反比;

（3）混合后溶液的浓度只由混配溶液的比例决定。

直接经验是小学生学习的基础，而肉眼看不出溶液混合的内在过程，但是我们可以借助一些相类似的直观情境，设置直观的问题帮助学生初步体会溶液混合问题中“交换”达到目标含量的思想。

1. 铺垫性直观问题

为帮助学生理解“溶液混合后，高浓度溶液为低浓度溶液提供溶质，低浓度溶液为高浓度溶液提供溶剂，以达到彼此的浓度相等”，利用直观性原则，为学生设置肉眼能看出并判断的问题。以下例子可供教师参考：

例1：如图6，小红家想养金鱼，现有两种金鱼优惠套餐。套餐1：买6只红色金鱼送2只蓝色金鱼;套餐2：买5只蓝色金鱼送3只红色金鱼。为了美观，小红最少需要买多少个套餐1、套餐2，才能使得蓝色金鱼与红色金鱼各占一半？

此问题，学生可以通过画图直观分析解决问题，由于套餐1和套餐2都只有8只金鱼，要使得蓝色金鱼与红色金鱼各占一半，那么购买后将金鱼重新分配，最终一定能使得每个套餐都是4只红色金鱼、4只蓝色金鱼。

由图6可知，套餐1的红色金鱼比4只多2只，套餐2的蓝色金鱼比4只多1只，那么套餐1多出的2只红色金鱼需要换为2只蓝色金鱼，而每个套餐2换1只蓝色金鱼为红色金鱼即满足红蓝金鱼各占一半，所以需要购买2个套餐2，才能提供2只蓝色金鱼与套餐1交换，使得每个套餐都是4只红色金鱼、4只蓝色金鱼。如图7。所以最少需要买1个套餐1、2个套餐2。

这一例子学生容易理解，通过“交换”达到目标含量的道理，但学生很难迁移到浓度问题中，因此，教师还可以进一步设计如下问题：

例2：如图8，为锻炼学生的实践能力，教师设计照料水培植物的比赛，为公平起见，教师为学生分发水培种子。现有两种质量相等装有种子的水杯，1号水杯有14颗种子，2号水杯有17颗种子，该教师想要每个杯中的种子都是15颗且总质量相等，至少需要多少个1号水杯、2号水杯才能配置想要的水杯呢？具体如何操作？

类似例1分析可知，需要1号水杯2个，2号水杯1个。要使总质量仍相等，则需要在2个1号水杯中各提取一颗种子质量的水给2号杯，即2个1号水杯都用一颗种子质量的水跟2号水杯换一颗种子。

在此例子中，教师应引导学生明白，要想使得种子的含量都是目标个数，需要提供种子个数比目标个数多的水杯型号以及比目标个数少的水杯型号，将多出来的种子跟需要种子的水杯换取等量的水才能使得水杯的总质量不变，而只有当所有水杯中多出的种子个数等于所有水杯中需要的种子个数，交换种子和水后才能刚好是种子含量都是目标个数且质量不变。

继续追问：上述两道例题中如果没有“最少”“至少”的字眼，还能如何解决问题？规律是什么？学生不难发现，只要例1中“套餐1的个数∶套餐2的个数=1∶2”，例2中“1号水杯的个数∶2号水杯的个数=2∶1”就能解决问题。从而为溶液混合问题中“混配的原溶液的质量比等于两原溶液与目标溶液的浓度差的绝对值的反比”这一事实埋下基础。

2. 直观表征，迁移应用

有了上述的例子，学生就不难理解微观分子溶液混合的问题了。在教学过程中，可以假设溶质没有溶解，将溶质与溶液分离，化抽象为具体，帮助学生直观分析。对于溶液混合问题，要求混合溶液的相关量（正推过程）显然会比求混合前溶液相关量（逆推过程）容易理解。在教学过程中应遵循循序渐进原则，先让学生接触求混合溶液相关量的类型题，再接触求混合前溶液相关量的类型题。以下例子可供教师参考：

例3：现有浓度为10%的糖水20克，加入浓度为30%的糖水30克，浓度变为多少？

要求混合溶液的浓度，则需知道混合后的溶质质量与溶液质量。学生不难理解混合溶液中溶质的质量为混合前各溶液的溶质质量之和，混合溶液的质量为混合前各溶液质量之和。根据浓度公式计算，混合溶液中溶质质量为20×10%+30×30%=11（克），溶液质量为20+30=50（克），从而混合溶液的浓度为■×100%=22%。

此例题已经蕴含“混配的原溶液的质量比等于两原溶液与目标溶液的濃度差的绝对值的反比”这一事实，但学生一般不会从这一角度解决问题，在此例题帮助学生挖掘这一知识点不合适。但通过对例3进行变式，有了上述直观例子做铺垫，在教师引导下学生不难发现这一知识点，理解这一知识点后，回头看例3就了一种解决方法，有利于学生加深理解。

例4：现有浓度为10%的糖水20克，再加入多少克浓度为30%的糖水，可以得到浓度为22%的糖水？

对于此类题型，可以假设溶质尚未溶解，分离溶质与溶剂，根据浓度可知溶质与溶剂的比例，从而画出图像，迁移例1、例2的直观经验帮助解题。

要得到浓度为22%的糖水，则10%的糖水、30%的糖水混合后浓度都变为22%。根据例2、例3的经验，学生已经有通过“交换”达到目标含量的思想。20克10%的糖水浓度要升高为22%，需要将（22%-10%）×20=2.4（克）水换为糖，而1克30%的糖水浓度要降低为22%，需要将（30%-22%）×1=0.08（克）糖换为水。

要使得10%的糖水与30%的糖水混合后浓度为22%，则需要30%的糖水多出的糖刚好等于20克10%的糖水多出的水，混合后30%的糖水多出的糖与10%的糖水多出的水“交换”，彼此的浓度才刚好为22%，混合后糖水的浓度自然为22%。如图9（黑色表示糖，白色表示水），因为1克30%的糖水只能提供0.08克糖进行“交换”，所以30%的糖水需要提供：2.4÷0.08=30（克）。

进而提问学：生如果浓度为10%的糖水为a克呢？

只要30%的糖水浓度降为22%需“交换”的糖刚好等于10%的糖水浓度升为22%需要“交换”的水，将两者混合即可各取所需，溶液成为22%的糖水，列出方程。设需要浓度为30%的糖水为b克，则（22%-10%）·a=（30%-22%）·b，即a∶b=（30%-22%）∶（22%-10%）。至此，学生就能理解发现“混配的原溶液的质量比等于两原溶液与目标溶液的浓度差的绝对值的反比”这一结论了。

对于溶液混合的问题，学生还应明白“混合溶液浓度只由被混配溶液比例决定”，对于此知识，举个数字与例3、例4不同的例子，学生对比便能发现。如果学生能明白“混配的原溶液的质量比等于两原溶液与目标溶液的浓度差的绝对值的反比”这一结论，自然也能明白其中的道理。混配溶液的比例一旦确定，浓度差比例就确定，由于混配溶液的浓度一定，混合溶液浓度介于两者之间，所以混合溶液的浓度也就确定了。

如此授课，既符合学生的认知发展，也能让学生对溶液混合问题的理解更加深刻。通过分离溶质、溶剂画图，“交换”溶剂、溶质达到目标浓度，有利于溶液混合过程在学生头脑中形成图形表征，获得更加直观的感受。