思维导图在初中数学概念教学中的应用

卫文平 秦永英

摘   要：思维导图是一种图形工具，思维导图可将复杂的、抽象的概念转化为直观的图示形象，帮助梳理数学概念成长史，构建数学概念网络体系，理清概念间的逻辑关系，提高学生数学运算能力，帮助学生总结解题思路。

关键词：思维导图;数学概念;核心素养

中图分类号：G633.6    文献标识码：A    文章编号：1009-010X（2021）05-0047-05

数学概念是人类对现实世界空间形式和数量关系的概括，是建立数学法则、公式、定理的出发点。数学概念教学的目标，就是要让学生理解概念，并能运用概念进行运算、推理和證明，进行数学思维和交流。学生要理解一个数学概念，就必须围绕这个概念构建一个网络体系，从概念的内涵和外延、概念的历史背景、概念间的联系，弄清概念的来龙去脉。思维导图这种高效的思维工具恰恰可以通过图文把概念间的隶属关系通过表格、图像、符号加以颜色建立记忆链接，根据记忆、阅读、思维的规律，将思维形象化、可视化，从而开发人类大脑的无限潜能。

一、初中数学概念教学中应用思维导图提升数学核心素养的重要性

（一）数学核心素养的内容

《普通高中数学课程标准》（2017版）定义数学核心素养为：学生应具备的、能够适应终身发展和社会发展需要的、与数学有关的关键能力和思维品质，包括六个方面：数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析。每一个核心素养有自身的独立性，在数学学习过程中，在发现、分析、解决问题的过程中，它们在不同的环节发挥不同的作用。

数学学科核心素养是数学课程目标的集中体现，是思维品质、能力、情感、态度与价值观的综合体现，是在数学学习和应用过程中逐步形成和发展的，这些数学核心素养既相互独立，又相互交融是一个有机整体。

（二）思维导图的优势

思维导图，英文是The Mind Map，又称心智导图、脑力激荡图、灵感触发图，是1971年由英国著名心理学家、教育学家东尼·巴赞（Tony Buzan）先生创造的一种终极的组织性思维工具，“思维导图是一种图形工具，可将复杂的、抽象的信息转化为直观的图示形象，帮助人们更好地进行观察、记忆、分析、决策、设计、创新等一系列思维活动”。

绘制思维导图可以通过软件和手绘两种方式，在思维导图的绘制过程中，学生使用不同颜色、图形、表格、线条、符号、关键字等元素，把静态的、杂乱的知识动态的生成，形成知识体系。绘制思维导图的过程简单而充满乐趣，不仅增强了学生对数学知识的掌握与理解，还有效激发了学生的学习兴趣，培养学生的数学核心素养。

（三）在数学概念教学中，通过思维导图提升数学核心素养的重要性

思维导图的运用可以帮助学生理清概念间的知识结构，创建知识体系，有利于学生对已有的问题进行全方位的思考和分析，提高学生解决问题的能力。不仅如此，思维导图的创建还能够提高学生的创造能力与逻辑思维能力，培养学生们专业的数学素养，为以后的知识创建和学习提供重要的帮助和引导，让学生在学习工程中学习变得更加轻松，充分提高课堂效率。

二、在数学概念教学中利用思维导图提升数学核心素养

思维导图的形式多种多样，数学课中常用的思维导图有八种类型，矩阵图、鱼骨图、逻辑图、括号图、桥型图、树形图、韦恩图。在绘制思维导图的过程中，学生的想象力与创造力常常让笔者受到启发。

（一）用思维导图梳理数学概念成长史

义务教育阶段，数学概念是随着学生的认知能力和生活经验不断引入的。例如“数的成长”是伴随着学生年龄与生活经历的增长而不断扩展的，小学阶段，为了数数和排序的需要引入自然数、整数，最初进行加、减运算，多个相同加数相加引入了乘、除运算;当测量结果不能用整数表示，或是“除不开”的时候引入了分数与小数，“不够减”时又引入负数。进入初中阶段，七年级学生，在地理学习过程中了解了海拔高度，生活中开始关注家庭经济生活中的收入与支出，负数与正数的引入成为必然，数系扩大到有理数。与“有理数对应”的“无理数”随之诞生，“实数”“虚数”也就接踵而来。按照学生的认知发展规律，用如下的思维导图能帮助学生理清“数的成长”过程。

XMind是一款实用的思维导图和头脑风暴软件，简单易用、美观、功能强大，拥有高效的可视化思维模式，为激发灵感和创意而生。作为一款有效提升工作和生活效率的生产力工具，受到全球百千万用户的青睐。利用XMind绘制的鱼骨图可以为学生梳理每一次数系的不断扩充。鱼骨图的鱼骨是分析数系扩充的思维线索，主分支显示数系的扩充的顺序，每个分支都代表每一类数产生的原因。子分支则在背后挖掘“为什么产生”“谁推动了数系的扩充”。因此，鱼骨图也被称为“因果图”。利用鱼骨图可以高效理清数系扩充的逻辑关系，让学生懂得数系的扩展伊始主要是由于实践的需要。正是为了解决实践中出现的问题，人们不断将数的领域加以扩展。讲述“数的成长”过程中的小故事，可以激发学生学习数学的兴趣，甚至让学生爱上数学，还可以增强学生的民族自豪感。例如，我国古代的《九章算术》是世界数学史上最早提出负数概念及正负数加减法法则的等等。

（二）用思维导图构建数学概念网络体系

学习数学概念的过程，就是为了将零散的数学概念存贮在大脑中，形成记忆，需要时即刻取出有用的那一部分进行解题、证明，解决生活中的问题。所以说，学生学习数学的过程就是理解概念、记忆概念的重要过程。初中数学概念分布在六册书的各个章节，都是零散的、碎片的，没有逻辑结构的，没能形成概念的体系。括号图（Brace Maps）是教与学过程中使用最为广泛的思维导图，常常通过图形、文字配以不同的颜色把数学概念串联起来，形成一张丰富全面的数学知识网。例如，在“实数”这一概念的教学过程中，思维导图能够全面、系统地展示“实数网”，使学生构建起严谨、通俗、直观的知识体系，培养学生自主学习的能力。还能帮助学生根据不同的分类标准理解实数、有理数、无理数、整数、分数这些概念的内涵与外延，将学生学过的所有的“数”全部清晰地呈现在眼前，学生在头脑中对实数体系有了更加完整的知识体系，减轻记忆负担形成永久性记忆，能达到事半功倍的完美效果。

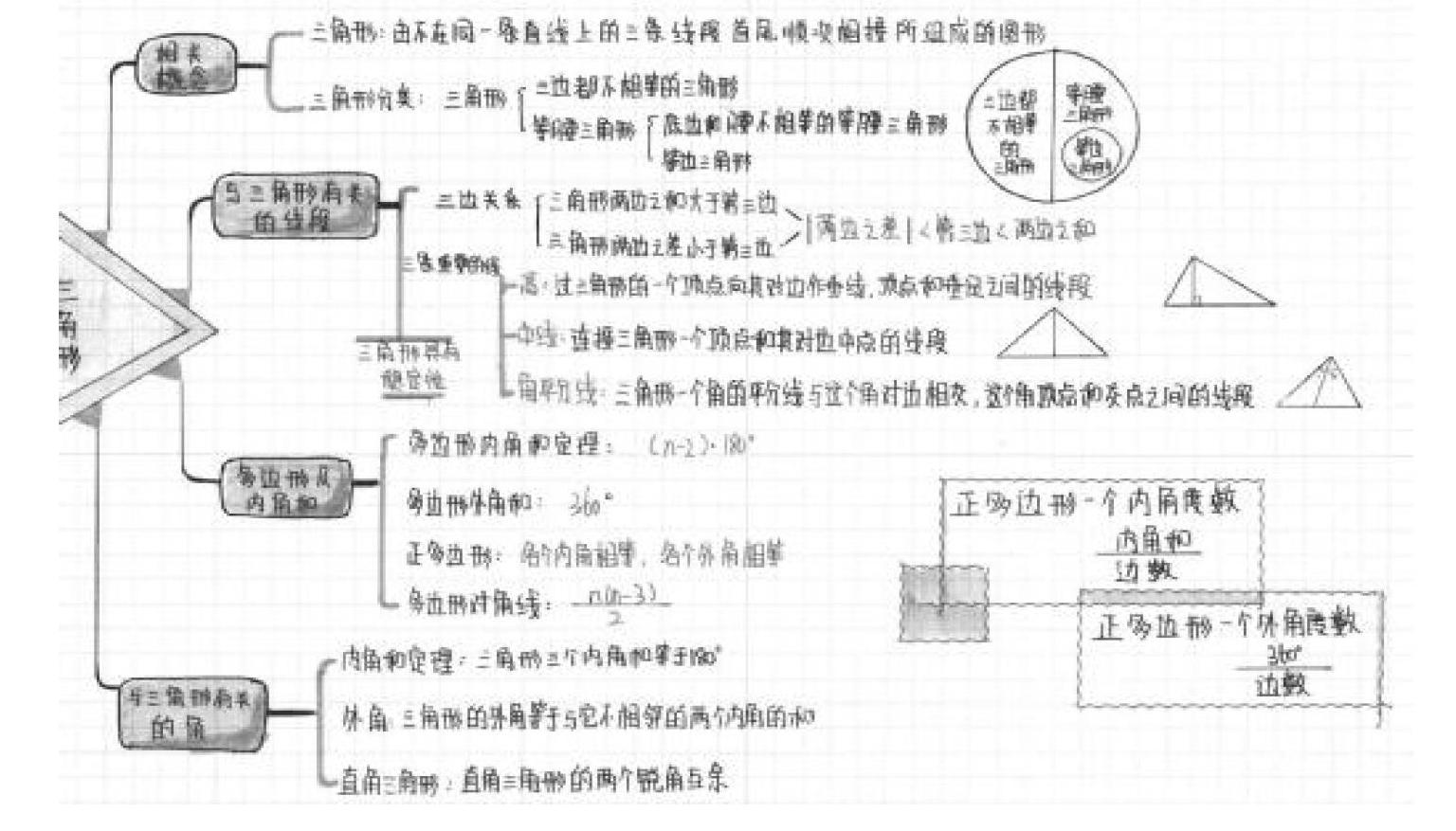
树状思维导图（Tree Map）是思维导图中最简单的形式，它把所有的信息都组织在一个树状的结构图上，每一个分支上写着不同的关键词或短语，树状思维导图又充满着色彩和图像，能够同时刺激人的两个半脑，让人思考、记忆、分析、触发灵感的同时发挥潜能。绘制树状思维导图可以培植学生脑中有“树”，心中有“网”，手中有“图”。例如，在学习三角形的有关概念时，学生绘制前面的树状思维导图，帮助同学整理与三角形概念有关的所有知识点，形成关于三角形有关概念的知识网。

（三）用思维导图理清概念间的逻辑关系

许多数学概念之间，存在着逻辑关系，只有弄清这些逻辑关系，学生才能清楚地理解概念。多重流程图（Multi Flow Maps）也称因果关系图，最初用来帮助学生分析一个事件产生的原因，和它导致的结果。创新应用多重流程图，它就变成了四边形分析“神器”，它的妙处在于可以帮学生对四边形、平行四边形、矩形、菱形、正方形做比较和对照，找到它们的差别和共同点，以及它们之间的逻辑关系。

在数学领域中，学者经常用平面上封闭曲线的内部代表集合，并用以表示各集合之间关系，这种图称为韦恩图（也叫文氏图）。韦恩图也是一种思维导图，用于显示元素集和重叠区域的图示。利用韦恩图可以给某些数学概念找一个“家”，例如可以用下面的韦恩图帮助学生理解平行四边形、矩形、菱形和正方形的关系，非常能锻炼学生的逻辑思维能力和思维的缜密性。

（四）用思维导图提高学生数学运算能力

针对新知识新概念推理出来的运算法则，老师可以利用整幅思维导图进行系统讲解，再让学生根据自己的理解整理和记忆画出自己的思维导图，帮助学生理解运算法则，能更好地达到教育教学的效果。泡泡图（Bubble Map）由很多泡泡组成，中间一个主题泡泡描述核心主题，周围的属性泡泡描述关于这个主题的属性，而且每個泡泡都和主题泡泡有一条线相连。这种图通常用于定义事物的属性或相应的联系。在幂的运算的教学中，当学习到“同底数幂相除”的时候，就可以用气泡图一起由幂的概念这一中心主题厘清“同底数幂相乘”“幂的乘方”和“同底数幂相除”的计算法则，从而提高学生的运算能力。

（五）运用思维导图帮助学生总结解题思路

思维导图不但可以帮助学生掌握数学概念之间的联系，而且建立概念网络体系，还可以帮助学生归纳总结解题的思维过程和知识难点，找到正确的解题方法和解题思路。因此，数学教师在教学中，可以利用思维导图指导学生分析和思考题目，建立已知条件和求解问题之间的“思维导图图”，将思维化无形为有形，将抽象的思维用具体可观的方式呈现。例如，（2019年河北中考题）已知光速为300000米/秒，光经过t秒（1≤t≤10）传播的距离用科学计数法表示为a×10n千米，则n可能为 （    ）

A.5    B.6    C.5或6    D.5或6或7

教师引导学生用如下的思维导图解答此题，通过绘制解题思维导图，学生思如泉涌、成竹在图。

综上所述，思维导图是一个思维工具，不但能融汇贯通在初中数学概念的教学中，还能应用到数学教学的所有课型教学中，教师要充分、合理、科学的运用它，熟练掌握它，让教学更轻松，更高效，让学习更有趣，更快乐。学生在绘制思维导图的过程中，既要琢磨如何呈现知识结构、概念体系，在提炼关键词的同时思考如何呈现自己的想法，在动手动脑过程中学生的阅读文本能力、分析概括能力、总结推理能力得到提高，推动学生数学核心素养的持续发展。画图往往能使学生集中注意力做一件事，促使学生主动参与知识形成的过程，符合中学生的心理特点和认知规律，有利于构建知识网络体系，发展逻辑思维能力。

参考文献：

[1]陈荣华.基于思维导图的形象思维训练模型构建[D].湖南师范大学硕士论文，2011.