立足在“1” 不止于“1”

钱振玉

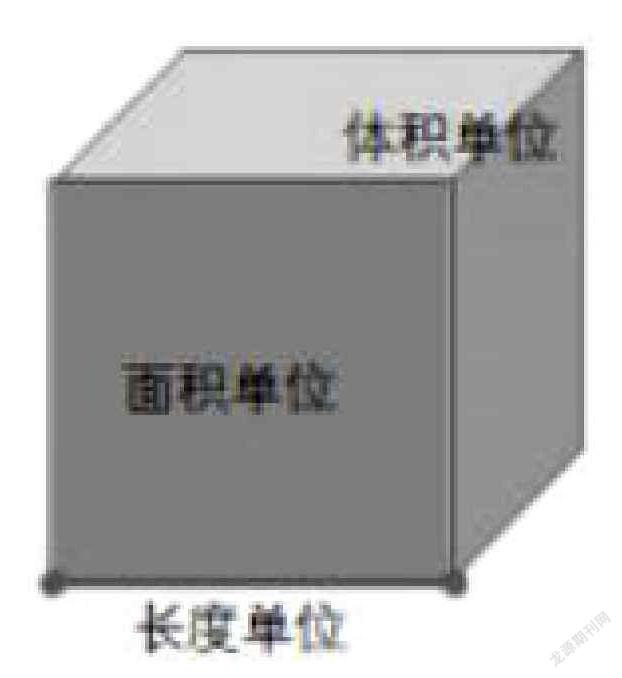
【摘要】量感是小学生重要的数学核心素养之一。本文结合体积教学，提出了在图形测量教学中通过多样操作、多维沟通、落实估测、想象推理等策略，培养学生的量感。

【关键词】量感  图形测量  单位量  累加量

【中图分类号】G623.5   【文献标识码】A 【文章编号】2095-3089（2021）13-0156-03

一、现象扫描：从一道监测题说起

笔者某年执教六年级的时候，期末质量监测卷中有这样一道选择题：“一个游泳池里大约能盛水（    ）立方米。”备选的答案有：A.20  B.200  C.2000  D.20000。考试结束进行典型错题统计，全班49位同学中有21人选错，而全校六年级共144名同学选错，占六年级总人数293人的49.1%。老师们在分析错误原因的时候，不约而同地认为，学生量感模糊是造成错误的主要原因。

在平时的教学中，我们不难发现：和数感相比，小学生的量感总体不是很好。在常见的量中，学生对“分、秒”“厘米、分米”等常用单位的感悟相对较好，而对“时”“千米”“千克、吨”等大单位的感知偏差较大，至于像“九寨沟是世界自然遗产，面积大约是720（    ）”这样的填空题应该选“公顷”还是“平方千米”则是完全没有概念，有的学生只是记住了教材中的一些数据和例子。相关学者的研究[1]也表明，学生对时间、长度的感觉相对较好，对面积的感觉较差，最差的是体积、容积的感觉。

量感的培养离不开量的教学，在课堂教学中则主要集中在计量单位的教学。但在实际教学中，大部分教师重视学生单位换算的能力和正确选择计量单位的能力，而忽视量感的培养，学生的量感普遍模糊。

那么，什么是量感？培养小学生的量感有什么价值？造成小学生量感模糊的原因，除了教学方式外还有哪些？如何在教学中帮助学生明确计量单位内涵，理清序列、有效培养量感呢？本文试以体积为例，对图形测量教学中量感的培养策略作一粗浅探讨。

二、深层剖析：量感的内涵和小学生量感模糊的原因

（一）量感的内涵和价值

一般来说，量感首先是建立量的概念、明确计量单位，在小学图形测量中主要就是指理解“长度、面积、体积（容积）”的含义，能通过视觉或触觉把握“1厘米有多长”“1平方厘米有多大”“1升的大小和重量”……;其次是在不借助工具的情况下直接估测某个事物的量的大小，或者将某个量和具体的事物相吻合的感觉。

量感的培养，有助于学生学会用数学的眼光分析问题，快速判断实際问题解答结果的合理性，增强思维的敏捷性和批判性，感受数学的应用价值，提高学生的数学素养。

（二）小学生量感模糊的原因

造成小学生量感模糊的原因主要有以下三个层面：

教材层面：与数的知识相比，量的内容和课时非常少;在要求上偏向重视于精确测量和计算，忽视对量的感悟和推断，估测的内容过少;选用的素材很多远离学生生活实际;教材内容呈现方式比较单一。

学生层面：受年龄限制和生活影响，小学生对基本计量单位有一定的感悟，对大单位的感知则不全面、不精确，有的甚至几乎没有生活经验;在图形方面空间缺乏空间想象，平面和立体转换困难，动手操作和实践探索的经验和能力都比较欠缺。

教师层面：教师的教学中普遍能重视计量单位的教学，重视“单位量”的感悟和内化，但往往忽视对“累加量”的体验和积累，而且缺少课后的运用，不能使学生持续感知和内化;同时由于量感的评价没有明确的要求和标准，也导致了教师一定程度的忽视。

三、实践建构：图形测量教学中量感的培养策略探索

张奠宙先生说：“测量，不仅仅是拿刻度尺去量测一条线段的长短（那属于物理学范围），数学测量的本质是给每一条线段以合适的数。”[2]测量的本质是“比较”，也就是先确定一个标准，用“1”表示，然后把需要测量的对象去和这个标准比较，数出含有标准的个数。因此测量的核心要素是度量的标准和度量的数值，量感的培养也要围绕着这两方面进行。

（一）立足在“1”：深刻感悟“单位量”

1.多样操作，形成空间表象

图形测量知识具有高度的抽象性，因此教师要善于引导学生进行各种操作，经历视觉、触觉、听觉等的多种体验，让学生在多感官的共同活动中，形成单位量的空间表象。

例如，教学《体积和容积单位》一课时，教师在“认识立方厘米”环节，设计了以下活动：

①想一想：闭上眼睛，想象1立方厘米是一个怎样的正方体;②拿一拿：从学具盒中，找出你想象的那个正方体;③量一量：用尺量一量小正方体的棱长，看找得对不对。④找一找：从学具盒中找出体积大约是1cm3的物体，和1cm3的正方体比一比。⑤做一做：你能用橡皮泥做一个大约1cm3的正方体吗？⑥比一比：展示学生作品，并和标准的1cm3正方体比一比。

人人参与的活动，先让学生定量刻画1cm3，然后通过想、拿、量、找等活动建立“单位量”的表象，接着在操作中经历“尝试—比较—调整—反思”的过程，促进“单位量”的切身体验和个性内化，最后形成清晰表象。

同样，教师在教学长度或面积单位时，可以设计“不用刻度尺，描出1厘米的线段”“徒手画出1平方厘米的小正方形”“用纸折出1平方分米的正方形”等数学活动，促使学生在不断调整中主动形成单位量的准确表象。

2.多维沟通，完善认知结构

图形测量中的长度、面积和体积，适用对象不同，但在构成要素和结构方法上有着紧密联系，学生比较容易混淆。因此，教学中要帮助学生区分和掌握不同计量对象的属性，理解计量单位之间的区别和联系，建构计量单位的认知结构。

例如，教学《体积和容积单位》一课时，在认识了三个体积单位后，教师设计了下面的比较：

师：同学们根据自己的经验，从以前学过的长度单位和面积单位展开联想和推理，得到了体积单位。现在，你能从这个1dm3的体积单位上找到长度单位和面积单位吗？从1cm3的小正方体上呢？

课件动态展示从正方体上剥离出一个面和一条棱的过程，说明这三类单位之间的联系非常緊密。

微视频：长度单位、面积单位和体积单位之间的联系，并明确它们不同的适用范围。

在此环节，教师借助实物直观展示和视频动态演示，让原本孤立的计量单位通过“体—面—线—点”的演示连接成知识网络，使学生感受度量几何的本质并形成多维量感。

（二）不止于“1”：不断丰盈“累加量”

量感的建立要从单位量“1”开始，但仅有单位量感，学生还是难以对具体物体或者图形的量做出正确估计，因此我们还要丰盈累加量的教学，充实量感培养。

1.落实估测，丰富参照体系

实践表明，学生对量的表象越丰富、参照物越多，学生对量的估计就越准确。因此，教师要帮助学生丰富“累加量”的表象，构建多样的参照体系，感受灵活选择参照标准的优越性，让量真正可感。

例如，教学《体积和容积单位》，课前请学生每人自制6个棱长1厘米的小正方体，准备好橡皮、火柴盒等物体。

（1）在认识1cm3后，同桌合作用自制小正方体摆出不同的长方体，说说体积分别是（  ）立方厘米，为什么？（2）用小正方体摆一个尽可能接近自己橡皮的长方体，估计并记住橡皮体积是（    ）cm3。（3）教师出示订书钉盒、火柴盒、木制图章、黑板擦等，学生观察并猜测体积是多少，再公布答案，比一比谁猜得更准。（4）有什么方法可以估计得更准一些？

小结：我们可以把常见物体作为参照物，熟记它们的体积。判断其他物体体积的时候，就可以和记住的参照物作比较。

上面的教学紧扣测量本质，使学生感悟测量的结果其实就是“1”（单位量）的累加;接着进行估测，在不断比较、调整、补充、完善中积累参照标准、修正估测经验，累积体积量感。

2.想象推理，提升思维品质

学生的现实生活中对大数量的接触很少，而图形测量方面的量也比较抽象，因此教师还要引导学生沟通计量单位间的联系，在学习方法的贯通中增强量感。

例如，教学《体积单位间的进率》一课时，教师请学生自制6个1cm3的小正方体和2个1dm3的正方体（其中一个无盖），设计以下的教学活动：

（1）猜想：根据长度和面积单位的进率，猜猜体积单位之间的进率可能是多少？（2）验证：小组合作，把1cm3的小正方体装入无盖的1dm3纸盒中，交流：小正方体个数不够多，你们是怎么摆的？你发现1cm3和1dm3的关系了吗？说说你的理由。（3）推理：刚才我们发现操作会有误差。你还能用其他的方法来说明1dm3=1000cm3吗？

小结：我们能根据长度单位间的进率和刚才操作的经验进行推理。再分别用操作和推理的方法，学习立方分米和立方米之间的关系。

（4）归纳：师生共同讨论归纳长度单位、面积单位和体积单位及进率。

体积单位进率较为抽象，教师引导学生“做”数学，经历猜想—验证—推理—归纳的过程，形成体积单位进率的清晰表象，并把长度单位和面积单位的感悟联系起来，形成整体量感，增强思维的逻辑性、深刻性。

教师还应该拓展学习的时间和空间，不断提供充实量感的训练。例如，教师可以布置课外“动手做”作业，让学生去估测生活中的饼干桶、鱼缸、电视机柜、浴缸、房间等的体积，再用长、正方体体积公式计算的结果进行检验调整，丰富累加量的感知，真正让量感从“1”走向“N”。

总之，体积量感的建立是一个漫长的过程，教师应该紧扣测量的本质，着眼于学生量感经验的积累，通过有效的教学方式，促进学生量感不断生长。

参考文献：

[1]周国蓉. 6年级学生量感现状调查与分析[D].西南大学，2014.

[2]张奠宙.深入浅出，平易近人——怎样测量长度、面积和体积[J].小学教学（数学版），2014（9）：4-6.