超网络能量研究与应用

刘胜久，李天瑞+，刘 佳，谢 鹏

1.西南交通大学信息科学与技术学院，成都 611756

2.四川省云计算与智能技术高校重点实验室，成都 611756

传统意义上的图及复杂网络一条边能且只能连接两个节点，描述图或复杂网络可以用等价的邻接矩阵或关联矩阵。但现实生活中往往出现一条边连接有多个节点的复杂系统，在这种情况下，传统意义上的图及复杂网络对此无能为力，需要用比通常意义上的复杂网络更为复杂的网络对其进行描述，这就是超网络。

超网络源于超图，其一条超边能连接任意多个节点的特性使得其能更好地刻画分析作品合著网络等其他形式的复杂系统[1-3]。描述超网络的常用方法是与超网络一一对应的关联矩阵，对超网络的研究使得超网络模型[4]、超网络维数[5]、超网络多重分形[6]等众多研究成果相继出现，带权超网络也逐步取代无权超网络，成为超网络研究新的热点。

图能量是代数图论及理论化学研究的重要课题，在分析烃类化合物的总π能量中有着重要作用。对图能量的研究是从对无向图的能量研究开始的[7]，并渐次推广到有向图[8]、混合图[9]等其他多种类型的图。无向图的图能量定义为其对应的邻接矩阵的特征值绝对值之和，一些基于类似定义的图能量的各种变种，如距离能量[10]、拟Laplacian能量[11]、关联能量[12]、斜能量[8]、Hermitian 能量[9]、匹配能量[13]、Laplacian 能量[14]、无符号Laplacian 能量[15]、Von Neumann 能量[16]、距离Laplacian 能量[17]、距离无符号Laplacian 能量[17]等先后提出，并取得很多重要研究成果。

大多数图能量及其变种均是基于矩阵特征值计算的，对大规模图并不适用。从分形维数出发，针对复杂网络提出了网络维数[18]，并应用于无向图及有向图，得到了对应的网络能量[19-20]。无向图及有向图的网络能量摆脱了矩阵特征值计算的繁琐操作，且与无向图的图能量、有向图的斜能量等多种类似能量之间存在着密切的关联。本文中，结合超网络的超网络维数，借助网络能量，尝试将超网络维数应用于超网络中，提出超网络的超网络能量，并分析超网络能量的若干重要性质。

1 预备知识

1.1 图能量

图是由节点及连接节点之间的边构成的。通常意义上，根据图中的边是否带有方向，可以将图划分为无向图、有向图、混合图三类。无向图的所有边均没有方向，有向图中的所有边都有方向，混合图中部分边有方向，部分边没有方向。对于无向图、有向图、混合图均有不同的能量计算方法。

对无向图G=(V,E)而言，其邻接矩阵可记为A(G)。其中，若G中节点vi与vj之间存在一条无向边，则Aij=Aji=1；若节点vi与vj之间不存在边，则Aij=Aji=0 。G的图能量E(G)定义为G的邻接矩阵A(G)的所有特征值绝对值之和，即有[7]：

式中，λ1A(G),λ2A(G),…,λi A(G),…,λn A(G)分别表示A(G)的各个特征值。

对有向图Gσ而言，可通过对无向图G的所有边赋予一个方向而得到，其斜邻接矩阵可记为S(Gσ)。其中，若Gσ中节点vi与vj之间存在一条有向边，则Sij=-Sji=1；若节点vi与vj之间不存在边，则Sij=Sji=0。Gσ的斜能量ε(Gσ)定义为Gσ的斜邻接矩阵S(Gσ)的所有特征值绝对值之和，即[8]：

式中，λ1S(Gσ),λ2S(Gσ),…,λiS(Gσ),…,λnS(Gσ)分别表示S(Gσ)的各个特征值。

对混合图M而言，可通过对无向图G的部分边赋予一个方向而得到，其Hermitian 邻接矩阵可记为H(M)。其中，若M中节点vi与vj之间存在一条有向边，则Hij=-Hji=i；若节点vi与vj之间存在一条无向边，则Hij=Hji=1；若节点vi与vj之间不存在任何边，则Hij=Hji=0。M的Hermitian 能量εH(M)定义为M的Hermitian 邻接矩阵H(M)的所有特征值绝对值之和，即[9]：

式中，λ1H(M),λ2H(M),…,λiH(M),…,λnH(M)分别表示H(M)的各个特征值。

无向图的图能量、有向图的斜能量、混合图的Hermitian 能量分别是无向图、有向图、混合图能量研究的基础，这些能量均是基于矩阵特征值计算得到的。一些其他类似的各种变种能量也不时出现，如新近提出的混合图的Hermitian 关联能量[21]等。

1.2 超网络

传统意义上的图及复杂网络一条边能且只能连接两个节点，超图及超网络的一条边可以连接任意多个节点。图是超图的子集，超图是图的超集，超网络也是传统意义上复杂网络的超集。超图及超网络能较图及复杂网络刻画更为复杂多样的复杂系统。

对于图及复杂网络来说，邻接矩阵及关联矩阵是两种主要的描述方法，这两种描述方法是等价的，可以相互转换，而且与原始的图及复杂网络也是一一对应的。超图及超网络也可以用类似的邻接矩阵及关联矩阵进行刻画，但超图的邻接矩阵与超图本身并不是一一对应的，一般情况下，对超图往往用与其一一对应的关联矩阵进行刻画。超网络由节点及超边组成，由于其一条超边可以连接任意多个节点，描述超网络的参数有节点度、节点超度及超边度等[4]。

定义1[22]对无权超网络H=(V,E)而言，|V|表示H中所含有的节点的数量，称为H的阶，|E|表示H中所含有的超边的数量，其关联矩阵C(H)是一个|V|×|E|阶的矩阵，其中，若节点vi包含在超边ej中，则有Cij=1，否则，Cij=0。

定义2[22]对无权超网络H=(V,E)而言，其密度是指H的所有超边包含的节点数目之和与其最多可包含的节点数目之和的比值，记为ρ(H)，即：

从分形维数的视角出发，可以得到无权超网络及带权超网络的超网络维数。无权超网络的超网络维数就是其对应的分形维数。一般情况下，研究的均是无权超网络。由于超网络的一条超边可以连接任意多个节点，即其节点度可以取任意数值，分析起来比较复杂，人们更多关注的是节点度相同的超图，即k-均匀超图。k-均匀超图中的每个超边均连接有k个节点。显然，2-均匀超图就是通常意义上的图。

定义3[4]对无权超网络H而言，其超网络维数HD(H)为其超边包含的节点数之和的对数值和节点数与超边数乘积对数值的比值的两倍，表述为：

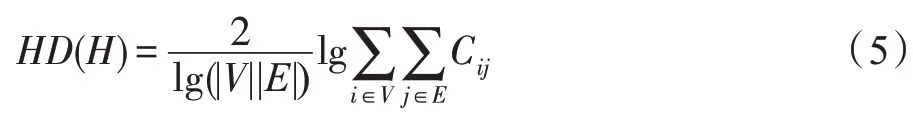
结合式（4），式（5）可改写为：

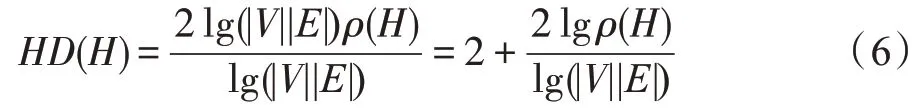
当H为k-均匀超图时，此时有：

定义4[5]对带权超网络H而言，其超网络维数HD(H)为其所有超边包含的节点权重之和与对应超边权重乘积和的对数值与节点权重之和与超边权重之和乘积对数值比值的两倍，表述为：

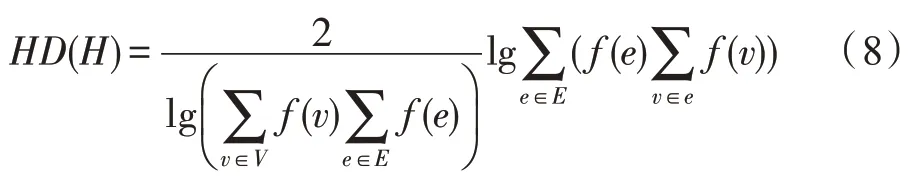
观察式（5）及式（8）可以发现，当带权超网络的节点权重f(v)及超边权重f(e)均为1 时，带权超网络即相当于无权超网络，此时式（8）退化为式（5）。

一般情况下，超图的超边数目与其节点数目不一定相等，也即超图的关联矩阵不一定是方阵，这将导致通过矩阵特征值计算得到图能量的常用方法不再适用，即通常意义上图能量的计算方法并不能直接推广应用到超图及超网络中。实际上，迄今为止，尚无针对超图及超网络能量的研究。

1.3 网络能量

网络能量是基于网络维数得到的。对无向图G=(V,E)而言，其中，|V|=n，|E|=m，其网络维数ND(G)表述为[18]：

于是，可以得到图G的网络能量NE(G)，表述如下[19]：

图G的网络能量NE(G)计算摆脱了矩阵特征值计算的低效操作，且与图G的图能量E(G)之间存在多个共同的上限，与距离能量、拟Laplacian 能量、关联能量、匹配能量等也存在较为密切的关联。

可以将无向图G的网络能量推广并应用到有向图Gσ，得到有向图Gσ的网络能量NE(Gσ)，表述如下[20]：

有向图Gσ的网络能量NE(Gσ)与有向图Gσ的斜能量ε(Gσ)及其原始图G的网络能量NE(G)之间也存在较为密切的关联。由于混合图是介于无向图与有向图之间的一类图，兼具无向图与有向图的特点，实际上，也可以将网络能量应用于混合图中。

由于无向图及有向图的网络能量均是通过网络维数而得到的，超网络也存在与之对应的超网络维数。下面，本文结合网络能量及超网络的超网络维数提出超网络的超网络能量，并对其进行深入的分析研究。

2 超网络能量研究

2.1 超网络能量

超网络的超网络维数是基于与其一一对应的关联矩阵定义的，借鉴网络能量，给出超网络H的超网络能量HE(H)，表述如下：

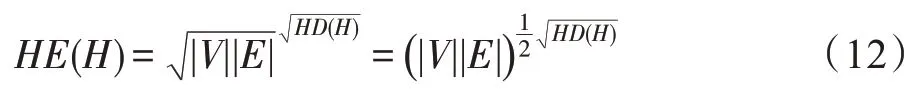
对超网络密度为ρ(H)的超网络H而言，其超网络能量HE(H)可以等价地表述为：

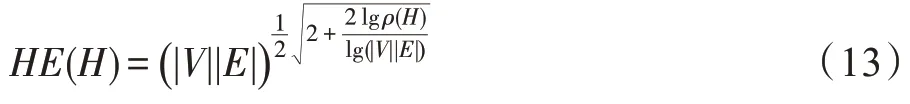
对k-均匀超图而言，其超网络能量HE(H)可以等价地表述为：

对式（14）进行分析，可以得到：

当|V|=|E|时，即节点数目与超边数目相等时，有：

若k=1，此时H一条超边只包含有1 个节点，即H为各个孤立的节点，此时：

观察式（17）可以发现，此时超网络H的超网络能量即为对2-正则图，即无向环图C|V|的每条边赋予方向所得到的有向图的网络能量。

若k=2，此时H一条超边只包含有2 个节点，即H为通常意义上的图，此时：

观察式（18）可以发现，此时超网络H的超网络能量即为对2-正则图，即无向环图C|V|的网络能量。

2.2 超网络能量分析

通过上面的分析可以发现，k-均匀超图的超网络能量与正则无向图及得到的有向图的网络能量之间的关联。于是，得到如下的定理。

定理1对2-均匀超图H=(V,E)而言，当|V|=|E|，其超网络能量HE(G)等于其对应的单圈图G=(V,E)网络能量NE(G)，即：

证明对单圈图G而言，其网络能量为：

结合式（18），即得式（19）。定理1 显然成立。

定理2对k-均匀超图H=(V,E) 而言，当|V|=|E|时，H的超网络能量HE(H)即是含有|V|个节点的k-正则无向图G的网络能量NE(G)。

证明根据超网络的超网络能量及无向图的网络能量的定义，定理2 显然成立。

定理3对k-均匀超图H=(V,E) 而言，当|V|=|E|时，H的超网络能量HE(H)即是对含有|V|个节点的2k-正则无向图G的每条边赋予方向所得到的有向图Gσ的网络能量NE(Gσ)。

证明根据超网络的超网络能量及有向图的网络能量的定义，定理3 显然成立。

至此，将k-均匀超图、k-正则无向图及2k-正则无向图得到的有向图通过超网络能量与网络能量联系起来。定理1、定理2、定理3 分别从不同的侧面论述了图是超图的子集，超图是图的超集。对无向图及有向图的网络能量的研究同样可以移植到同阶的超网络的超网络能量的研究中。下面，本文对超网络的超网络能量性质进行深入的分析研究。

3 超网络能量性质

上文通过对超网络的超网络维数及网络能量的分析研究，提出了超网络的超网络能量，下面对超网络的超网络能量性质进行分析研究。对于一般的超网络而言，计算其精确的超网络能量较为复杂，本文主要对超网络的超网络能量的下限及上限进行分析研究。先对超网络能量的下限进行研究。

定理4对超网络H=(V,E)而言，其超网络能量HE(H)的下限为0，即：

证明根据超网络能量定义，定理4 显然成立。

式（21）中等号成立的条件是H为零超图或空超图，即H不含有节点或超边。

一般情况下，非空超图至少含有一条非空超边，于是得到下面的定理。

定理5对非空超网络H=(V,E)而言，其超网络能量HE(H)的下限为1，即：

证明非空超网络至少含有一条非空超边，此超边至少连接有1 个节点。根据超网络能量定义，定理5 显然成立。

式（22）中等号成立的条件是H仅含有一条连接有1 个节点的超边。

下面对超网络能量的上限进行研究。

定理6对超网络H=(V,E)而言，其超网络能量HE(H)的上限满足下式：

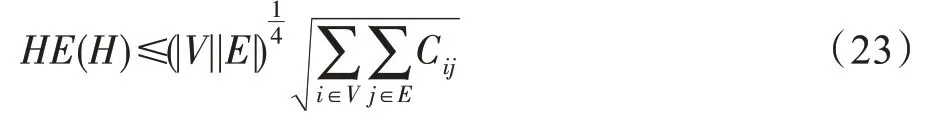
证明对超网络H的超网络能量HE(H)进行分析，有：

定理6 显然成立。

定理7对超网络H=(V,E)而言，其超网络能量HE(H)的上限满足下式：

证明对式（13）进行分析，由于超网络H的超网络密度0 ≤ρ(H)≤1，当ρ(H)=1 时，超网络H的超网络能量HE(H)取最大值，此时超网络能量HE(H)为：

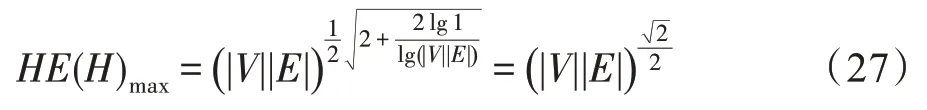
定理7 显然成立。

式（26）中等号成立的条件为超网络H的超网络密度ρ(H)为1，此时超网络H的每一条超边均连接有|V|个节点，即此时的超网络H为|V|-均匀超图。于是，可以得到如下的引理。

引理1k-均匀超图的超网络能量HE(H)的上限满足下式：

证明k-均匀超图中，k的最大值为k=|V|，代入式（14），即得：

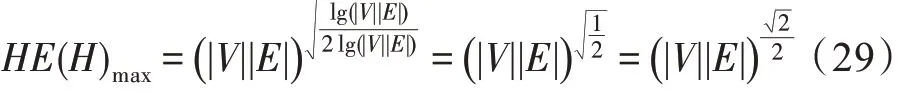
引理1 显然成立。

当超网络的节点数目与超边数目相等时，可以得到如下的引理。

引理2对超网络H=(V,E)而言，当|V|=|E|时，其超网络能量HE(H)的上限满足下式：

证明在式（27）中，令|V|=|E|，即得式（30）。引理2 显然成立。

其实，式（30）也是|V|阶无向图的网络能量的上限[19]。即当|V|=|E|时，超网络H的超网络能量HE(H)与对应的同阶无向图G的网络能量NE(G)具有相同的上限。

定理8对于n个超图H(i)(1 ≤i≤n)的Tracy-Singh积超图H(n)而言，H(n)的超网络能量HE(H(n))可以表述如下：

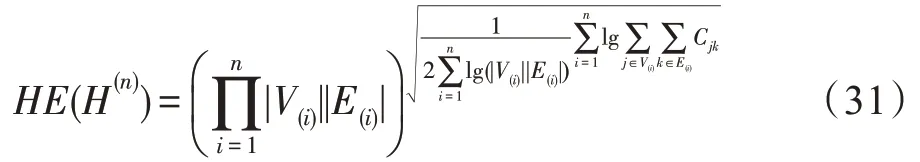
证明对于H(n)而言，其节点数|V(n)|、超边数|E(n)|、超网络维数HD(n)分别如下[4-5]：

根据超网络维数的定义，将式（32）代入式（12），即得式（31）。定理8 显然成立。

对一个初始超图的迭代Tracy-Singh 积超图进行分析，则可以得到如下的引理。

引理3初始超图H的迭代Tracy-Singh 积超图H(n)的超网络能量HE(H(n))是初始超图H的超网络能量HE(H)的n次方，即：

证明对于H(n)而言，其超网络维数HE(H(n))等于H的超网络维数HD(H)。H(n)的节点数|V(n)|、超边数|E(n)|、超网络维数HD(n)分别如下：

根据超网络维数的定义，将式（34）代入式（12），则有：

引理3 显然成立。

特别的，当初始超图H的超网络密度ρ(H)为1时，可以得到如下的引理。

引理4对于超网络密度为1 的初始超网络而言，其迭代Tracy-Singh 积超图H(n)的超网络能量HE(H(n))可表述为：

证明超网络密度ρ(H)为1 的超网络H具有最大的超网络能量。初始超网络H的超网络能量HE(H)为：

根据引理3，迭代Tracy-Singh 积超图H(n)的超网络能量HE(H(n))为：

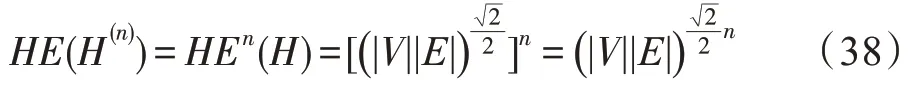
引理4 显然成立。

本文对一般情形下的超网络进行分析，则可以得出如下的结论。

定理9密度为ρ的超网络H=(V,E)的超网络能量上限满足下式：

证明对式（13）进行分析：

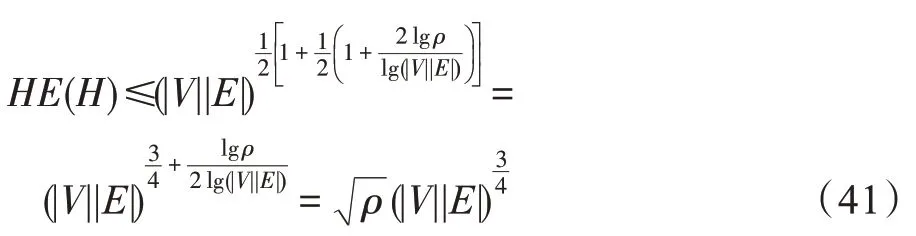
定理9 显然成立。

当超网络为k-均匀超图时，可以得到如下的引理。

引理5对密度为ρ的k-均匀超网络H=(V,E)而言，其超网络能量HE(H)的上限满足下式：

证明在密度为ρ的k-均匀超网络H=(V,E)中，有ρ|V||E|=k|E|，即有：

将式（43）代入式（39），即得式（42）。引理5 显然成立。

此外，当超网络的节点数目与超边数目相等时，可以得到如下的引理。

引理6对密度为ρ的超网络H=(V,E)而言，当|V|=|E|时，其超网络能量HE(H)的上限满足下式：

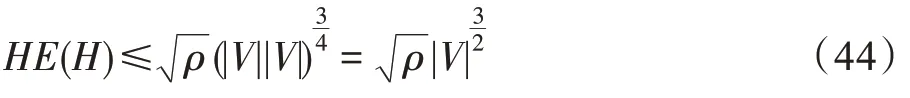
证明在式（39）中，令|V|=|E|，即得式（44）。引理6 显然成立。

其实，式（44）也是|V|阶无向随机图Gn(ρ)的网络能量的上限[19]。即当|V|=|E|时，密度为ρ的超网络H的超网络能量HE(H)与对应的同阶且连接概率为ρ的无向随机图G的网络能量NE(G)具有相同的上限。

定理10对超网络H=(V,E) 而言，当时，其超网络能量HE(H)的上限满足下式：

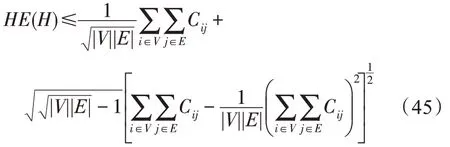
证明根据式（12）所示的超网络的超网络能量的表述，欲证定理10，只需证下式即可：

令f(x)=，可以发现，当x≤n时，f(x)为增函数，当x≥n时，f(x)为减函数，即f(x)的一阶导数f′(x)在区间(-∞,n)为非负数，在区间(n,+∞)为非正数：

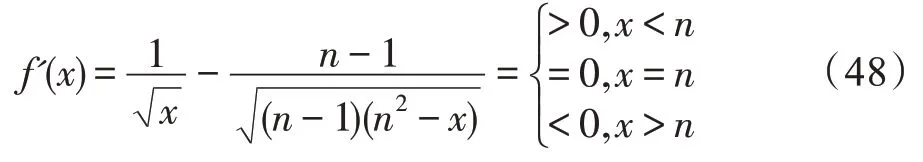
当且仅当x=n时，f(x)的一阶导数f′(x)=0。于是，有：

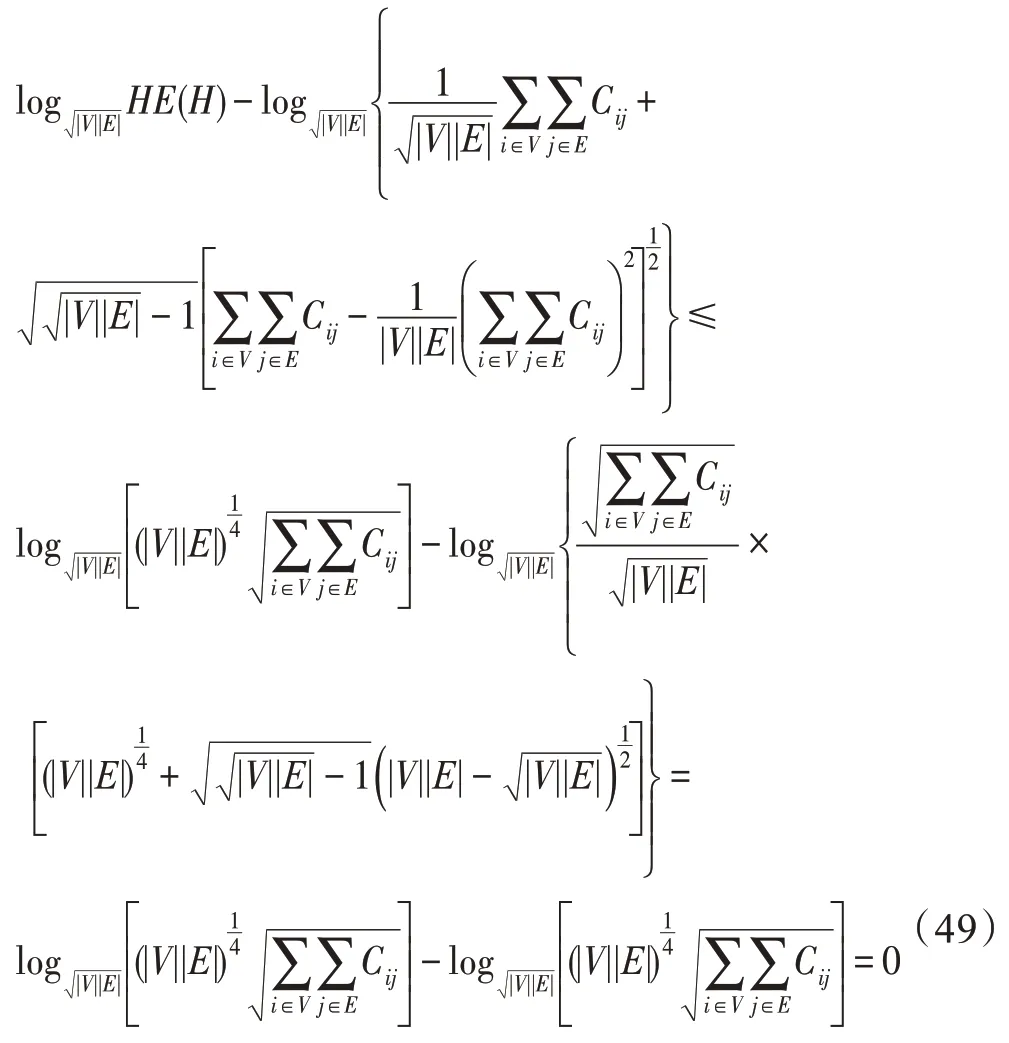
定理10 显然成立。

将式（4）代入式（45），可以得到如下的引理。

引理7对密度为ρ的超网络H=(V,E)而言，当时，其超网络能量HE(H)的上限满足下式：

证明将式（4）代入式（45），即得式（50）。引理7显然成立。

进一步，当超网络的节点数目与超边数目相等时，可以得到如下的引理。

引理8对密度为ρ的超网络H=(V,E)而言，当且|V|=|E|时，其超网络能量HE(H)的上限满足下式：

证明将|V|=|E|代入式（50），即得式（51）。引理8 显然成立。

4 结束语

超网络由节点和超边组成，其一条超边能连接任意多个节点的特性使得其比通常意义上的复杂网络更为复杂，也能对更多的复杂系统进行刻画。图能量已在无向图、有向图、混合图等多种不同类型的图中得到较为成功的应用，在代数图论及理论化学等领域有着广泛的应用前景。传统意义上的图能量基于矩阵特征值计算，无法很好地推广应用到大规模图中。目前尚无对超网络的能量的研究。先前将网络能量应用于无向图及有向图中，规避了矩阵特征值计算的繁琐操作，并论述了网络能量的重要性质及与其他类似能量之间的关联。本文将网络能量应用于超网络中，结合超网络的超网络维数，提出了超网络的超网络能量，并分析了超网络能量的若干重要性质，给出了超网络的超网络能量的上下限及与图的网络能量之间的关联。后续工作的重点在于对超网络的超网络能量进行深入的分析，并尝试对有向超网络、混合超网络及带权超网络等其他类型超网络的超网络能量进行研究。