构建函数解不等式

顾冬梅

(江苏省海门市第一中学 226100)

函数与方程、化归与转化思想是高中数学的重要思想，构建函数是这两种思想的体现.在高中数学教学中有一类是导数与不等式相结合问题，学生感到有点棘手，本文针对常出现的三类不等式怎样构造函数作了一点总结，希望对大家有所启发.

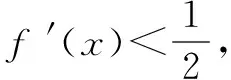
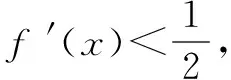
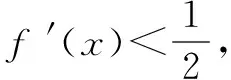
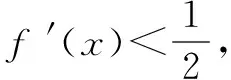
总结这类问题将导数不等式与所求不等式形式相结合投石问路构造新函数，有些表面上看似复杂，但若用整体的思想看待问题，抓住本质，问题就迎刃而解了.而基于例题的变式又是将解题的关键由点及面、举一反三的效果，真正训练了学生的感悟深度和效度.

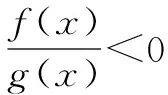
变式设f(x)是R上的奇函数，在区间(-∞，0)上有xf′(x)+f(x)<0且f(-2)=0，求不等式xf(x)<0的解集.

分析例2中突破口是f′(x)g(x)>f(x)g′(x)，移项后得f′(x)g(x)-f(x)g′(x)>0.

例2的变题中有xf′(x)+f(x)<0，根据求导的乘法法则自然会构建函数h(x)=xf(x),构建的函数完全与所求不等式xf(x)<0吻合.

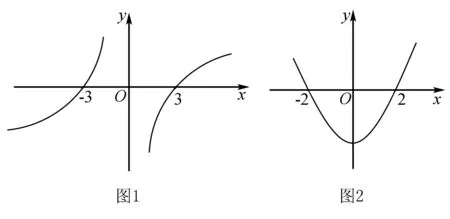
解析构建函数h(x)=xf(x)，在(-∞，0)上有xf′(x)+f(x)<0,则h(x)=xf(x) 在(-∞，0)是单调减函数，且由f(x)是R上的奇函数得h(x)在R上为偶函数，由f(-2)=0得到h(-2)=0.有了函数的单调性及奇偶性，不妨画出函数好h(x)图象(如图2)，得xf(x)<0的解为(-2,2).

总结例2及其变题都是以乘法、除法的求导法则为突破口构建相应函数.我们要通过问题的形式让学生自发地总结求导的一般特点和一般方法，让学生在感悟中总结，总结中提升.

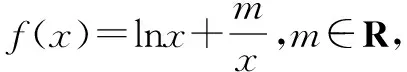
分析本题将不等式f(x2)-f(x1)f(x2)，那么f(x)就是在这个区间上的减函数)，不妨构建g(x)=f(x)-x.

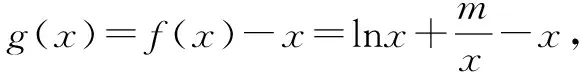
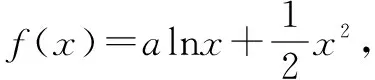
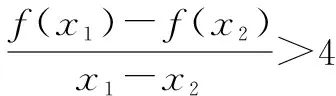
总结例3及其变式都是紧紧抓住函数单调性的定义，因为题目中涉及x1，x2，所以比较自然地联系函数的单调性的定义，根据定义把已知进行条件变形，那么构建函数也就不难了.

构造函数本就是解决问题的一种技巧，它考查了学生的观察和动手能力，本文通过三个例题讲述了在导数知识中需要构建函数解不等式问题.但是用构建函数解不等式或证明不等式的题目大量存在，还需要学生进一步思考和总结.