巧妙提问,助力建构高效课堂
尤维明

[摘 要] 新课标引领下,教师精准、恰当且艺术性地提问,可以激发学生的求知欲,进而助力高效课堂的建构. 文章以具体教学实践为例,呈现以下助力建构高效课堂的提问策略:理解学生,以合理问题引探究欲望;把握本质,以核心问题促思维生长;整体把握,以技巧性提问引探究学习.
[关键词] 提问;高效课堂;问题导学
新课标引领下,教师精准、恰当且艺术性地提问,可以激发学生的求知欲,进而助力高效课堂的建构. “问题导学”是近年来广受师生欢迎的教学方式,这种方式有效沟通了教师的教学智慧与学生的数学思维,构建了学思创共生的高效课堂. 但在具体的教学实践中,笔者发现教师的课堂提问仍然存在着诸多问题,导致学生的数学学习呈现出浅层化、被动化的状态. 高效数学课堂呼唤着一种有效提问方式,那么,如何设计问题才能为学生的数学思维提供方向?如何提问才能提高课堂教学效率?笔者根据这几年的潜心研究和深度思考,初步得出以下几点策略.
理解学生,以合理问题引探究欲望
数学课程致力于学生数学核心素养的形成,而课堂是师生双方共同参与的动态过程,教师需要用好为学生数学学习提供养料的数学教材,从学生的角度去分析、理解、挖掘教材,在读懂教材的基础上,了解学生的认知结构,为课堂提问探寻合适的出发点,以合理的问题设计引发学生的探究欲,才能提高问题的有效性,进而提高课堂效率[1].
案例1三角形的中位线.
师:大家一起回顾一下,在学过的三角形中哪些线段比较重要呢?
生1:三角形的三条边、高.
生2:角平分线、中线.
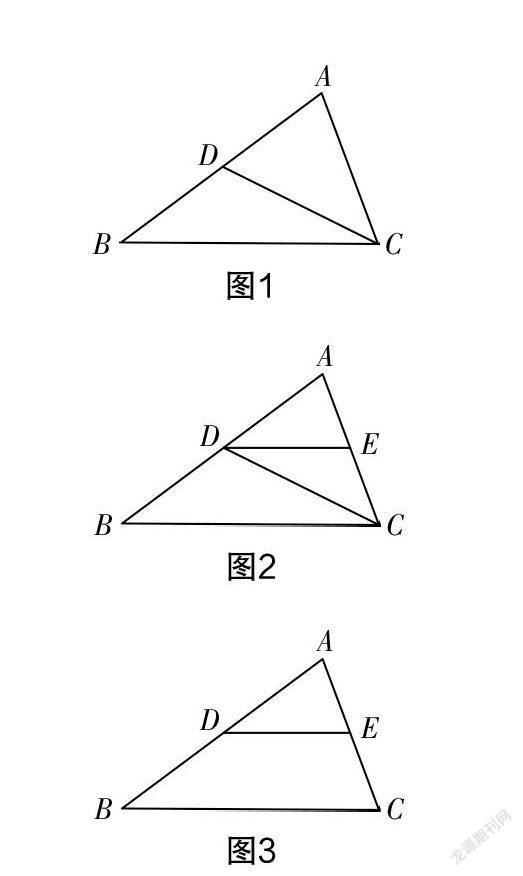
师:那我们一起来看这个问题,如图1,已知△ABC中,点D平分边AB,连接CD,可以得出什么结论?(教师PPT展示问题)
生3:△ADC的面积等于△BDC的面积.
师:刚才生3所阐述的结论非常重要,可以总结为“三角形的中线将三角形分为面积相等的两个三角形”.
师:那以上问题再添加条件“点E平分边AC”,连接DE,又可以得出什么结论?(教师PPT展示图2)
生4:这样一来,DE就可以看作△ADC的中线,因此△ADE和△CDE的面积相等.
师:现在,我们再把图2中的线段CD去掉,又可以得出什么结论?(教师PPT展示图3)
生5:△ADE与四边形BCED的面积之比为1 ∶ 3.
师:真棒!从而我们可以得出以下结论——连接三角形两条边中点的线段,可以将三角形分为面积之比为1 ∶ 3的一个三角形和一个四边形. 那么,谁能来命名一下这样的一条特殊线段呢?它是否还具有其他性质?这就是我们今天要学习的……(最后出示概念)
设计意图 每一个知识点都不是孤立的,它不仅是前面所学知识的延续,也是新知的铺垫,所以在学习新知时,教师应致力于引领学生认知的迁移,优化学生的认知结构. 以上案例中,问题的设计基于学生熟悉的三角形,起到引疑、激疑的作用,揭示研究的本质. 通过问题串的一一解决,学生经历了从“中线”向“中位线”的过渡,对概念有了初步的感知,为进一步高效建构新概念奠定了良好的基础. 这样的设计低起点、高立意,引发了学生的兴趣,更符合学生的认知水平,让学生的探究活动自然深入,使得概念的自主建构水到渠成,使学生的思维得到了锻炼和发展.
把握本质,以核心问题促思维生长
随着课程改革的推进,教师的教育理念逐渐更新,课堂教学行为也得到了较大的改进. 当然,要想使得课堂教与学的关系真正到位、课堂教学效益最大化,以核心问题引领数学课堂才是关键[2]. 事实上,找准一节课的核心问题,才能把握住一节课的“课眼”,才能让学生的思维具有聚焦点,才能让学生的学习拥有“靶心”. 因此,教师应在课前进行这样的思考:本节课中,学生需要学些什么?学生真实的认知起点在哪里?可能会产生哪些认知困惑?新旧知识间的冲突在哪里?如何才能让学生产生学习新知的需求?如何才能让学生从根本上认识和理解这些知识?只有教师对以上问题有了深刻的把握,再精心设计核心问题,才能让问题成为激励学生参与课堂的催化剂,成为促进学生向更高认知水平前进的助推器,从而真正提高课堂效率. 像这样通过创设大问题来构建大空间,让教学内容“问题化”,能让教学更有方向、更具活力、更加高效.
案例2勾股定理.
师:当直角三角形三边都是整数时,这样的三个整数就是一组勾股数,如3,4,5这三个数就构成一组勾股数. 你还能说出哪些勾股数呢?
生1:6,8,10;9,12,15.
师:你是如何探寻勾股数的呢?
生1:当n是正整数时,诸如3n,4n,5n的三个数.
师:方法不错!其他同学如何探寻的呢?
生2:观察以上多组勾股数,我发现3=4+5,5=12+13,7=24+25,从而猜想得出“当n是奇数时,n2=+”.
师:很棒,还有没有更一般的方法呢?(学生开始专注地进行作图、思考、探讨)
师:已知△ABC的三边长分别是a,b,c,有a=m2-n2,b=2mn,c=m2+n2,且m,n为正整数,m>n,那么△ABC是直角三角形吗?为什么?
生3:可以利用勾股定理的逆定理a2+b2=c2证明△ABC是直角三角形.
师:很好,尽管我们还没有找寻到更一般的方法,但这一问題让我们的探究有了准确的方向,谁能来具体阐述呢?
生4:取任意两个正整数m和n,且m>n. 再构造3个数a,b,c,使得a=m2-n2,b=2mn,c=m2+n2,分别以a,b,c为三边的三角形一定是直角三角形,那么,a,b,c则构成勾股数.
师:好,那你能举例验证一下吗?
生4:当m=5,n=4时,a=m2-n2=9,b=2mn=40,c=m2+n2=41,则9,40,41就是勾股数.
师:哇,此处必须有掌声啊!事实上,前面就是在探究x2+y2=z2的正整数解,符合这样要求的正整数就是勾股数,对吗?
生(齐):对!
师:那么,当整数n>2,与x,y,z相关的不定方程xn+yn=zn是否有正整数解呢?
生5:应该有,但我不会找.
师:的确,老师也感觉有解,但数学是需要依据的,并非凭感觉,不过至今我们还没有找到这样的正整数. 其实,早在17世纪……
设计意图 本案例中,教师站在核心问题设计的角度,以问题“你是如何探寻勾股数的?”设置认知冲突,让学生的数学思维有了方向,学生从被动接受转变为主动思考,从“存在勾股数——一类勾股数——求勾股数的方法”的方向进行猜想、思辨、論证和反思,最终生成正确的结论. 由于有核心问题的指引,每个学生都可以有依据地进行思考并探寻解决问题的策略,这一过程就是积极思考、主动建构的过程.
整体把握,以技巧性提问引探究学习
教师提问的技巧影响着课堂教学的效果,这一点是毋庸置疑的. 不少教师课堂提问习惯于“随意问”“惩罚问”,长此以往,学生对问题的专注力和兴趣度逐渐减弱,直至消失,使得课堂教学效率低下[3]. 可见,技巧性提问对于课堂教学十分重要. 那么,如何提问才能让课堂教学更具可操作性呢?笔者认为主要需要做好以下几点:准确把握提问时机、合理分配答问的对象、消除学生的畏难心理、给足学生思考时空、善于倾听学生的心声等,只有这样恰到好处地发问,才能让课堂提问发挥最大优势,成为师生交流进步的载体,助力高效数学课堂的建构.
案例3幂的乘方.
学习“幂的乘方”时,笔者抛出问题让学生计算(3-2)5,不少学生顿感难度过大,并提出“负指数幂还没有学过”的抗议. 而事实上,幂的乘方法则学生已经学过,结合已学知识进行联想是不难得出答案的. 于是,笔者笑眯眯地看着学生说:“难度是挺大的,但是看到这个问题你有没有一点想法呢?可以试一下,说错了没关系的,我们一起讨论……”
设计意图 教师的真诚鼓励和耐心等待推动了学生的积极思考,学生很快根据“底数不变,指数相乘”这一法则探寻到答案.
总之,在教学过程中,教师应深刻把握提问的要旨,设计高质量的数学问题,引领学生开展数学探究活动,发展学生的数学核心素养. 追求以问题导学为导向的数学课堂教学,其实就是要关注学生的数学学习和数学探究,让课堂提问从“表层”走向“深刻”. 善于运用问题引领教学,教学过程才能精致,教学环节才能简约,教学方式才能活络,课堂教学才能高效.
参考文献:
[1]温建红. 论数学课堂预设提问的策略[J]. 数学教育学报,2011,20(3).
[2]李鹏,傅赢芳. 论数学课堂提问的误区与对策[J]. 数学教育学报,2013,22(4).
[3]温建红. 数学课堂有效提问的内涵及特征[J]. 数学教育学报,2011,20(6).

