“一核四维”，强化运算能力、促进深度学习

陶蕊 谈玉琴

[摘  要] 随着知识创新时代的到来，深度学习正成为基础教育改革的新趋势. 深度学习要求学习者掌握非结构化的深层知识，并进行批判性高阶思维的打造、主动的知识构建、有效的迁移应用及真实问题的解决，进而实现问题解决能力、批判性思维、创造性思维、元认知能力等高阶思维和能力的发展. 数学运算是新课标六大数学核心素养之一，是促进深度学习的有效载体. 文章以强化圆锥曲线的运算能力、促进深度学习为核心，从四个维度（运算根基、运算方向、运算速度、运算经验）浅谈圆锥曲线教学中强化运算能力、促进深度学习的实践与探索.

[关键词] 运算能力;深度学习;圆锥曲线

富兰在《极富空间》一书中提出：“深度学习的目标是：使學生获得成为一个具有创造力的、与人关联的、参与合作的终身问题解决者的能力和倾向.”深度学习既是一个学习个体主动建构知识的过程，又需要学习主体之间将知识和信息进行交换和重组. 深度学习是在具体的学习过程中实现的. 数学运算不仅是解决数学问题的必备条件，也是促进深度学习的有效载体.

[?]概念的界定

（1）数学运算是指在明晰运算对象的基础上，分析运算条件、依据运算法则解决数学问题的过程. 主要包括理解运算对象、掌握运算法则、探究运算方向、选择运算方法、设计运算程序、求得运算结果等.

（2）深度学习. 布鲁纳说过：“学习存在表层和深层两个过程，掌握知识经验的过程是学习的表层，而通过掌握知识，形成一定的思考方式、学习态度，增强解决问题的能力和自信才是学习的深层过程，真正的学习包括获取知识、发展能力和形成态度.”所以，深度学习是相对于浅层学习而言的，是一种基于理解的学习，因此理解批判性思维、整合学习内容、构建知识体系和有效进行知识迁移的学习活动，是构建高效课堂、内化核心素养的重要途径.

[?]圆锥曲线教学中强化运算能力的目的与意义

著名的数学家波利亚指出：“掌握数学就意味着善于解题.”运算能力是善于解题的必备条件，是高中生应该具备的一种重要的数学能力. 圆锥曲线是高考数学的命题热点，从近几年浙江省高考数学试卷的结构来看，2道填空题和选择题小题，1道解答题大题，分值大概30分左右. 解题的特点是入口很宽、方法灵活、运算量大，但是很多学生“败”在了运算上，得分率偏低，所以强化圆锥曲线的运算能力显得尤为重要！

（1）激发学习兴趣，提升运算素养.“成功的教学不是强制，而是激发学习兴趣.”运算来源于学习活动本身，为学生提供了一种情境，使其在多元的运算剖析与评价活动中，克服畏难心理、增强学习兴趣，强化运算能力、促进深度学习.

（2）优化思维品质，发展创新能力.美国心理学家吉尔福特指出：“人的创新能力必须要有敏锐的洞察力，要能够透过事物的表面现象把握其内在本质特性.”深度剖析运算算理，厘清运算本质;领悟运算经验，优化思维品质，发展创新能力.

（3）教学相长，促进教师专业发展.美国教育心理学家波斯纳提出了一个教师成长公式：教师成长=经验+反思. 通过强化运算能力的研究促进教师反思，反思学生的“学”、反思自己的“教”，在反思中改进教学策略，提升教学效益，促进专业发展.

[?]圆锥曲线教学中强化运算能力、促进深度学习的实践与探索

荷兰著名的数学教育家弗赖登塔尔曾指出：“数学教育方法的核心是学生的再创造.”圆锥曲线中蕴含着丰富的运算方法与技能，是培养学生运算素养和再创造能力的重要载体. 教师要整合资源、搭建平台，从夯实运算根基、指明运算方向、提升运算速度、巩固运算经验四个维度，帮助学生在运算的过程中用自己的体验、自己的思维，重新创造有关的数学知识，提升运算能力、促进深度学习.

1. 强化概念，夯实运算根基、促进深度理解

李邦河院士说过：“数学根本上是玩概念的，不是玩技巧，技巧不足道也.”圆锥曲线的概念是其一切几何性质的“根”与“源”，是解几何综合题的重要背景，也是高考数学试题考查的重点. 教学中要挖掘概念的深层次内涵，从更高的层面寻求深化的认识过程，搭建知识框架、感悟数学思想，夯实运算根基、促进深度学习.

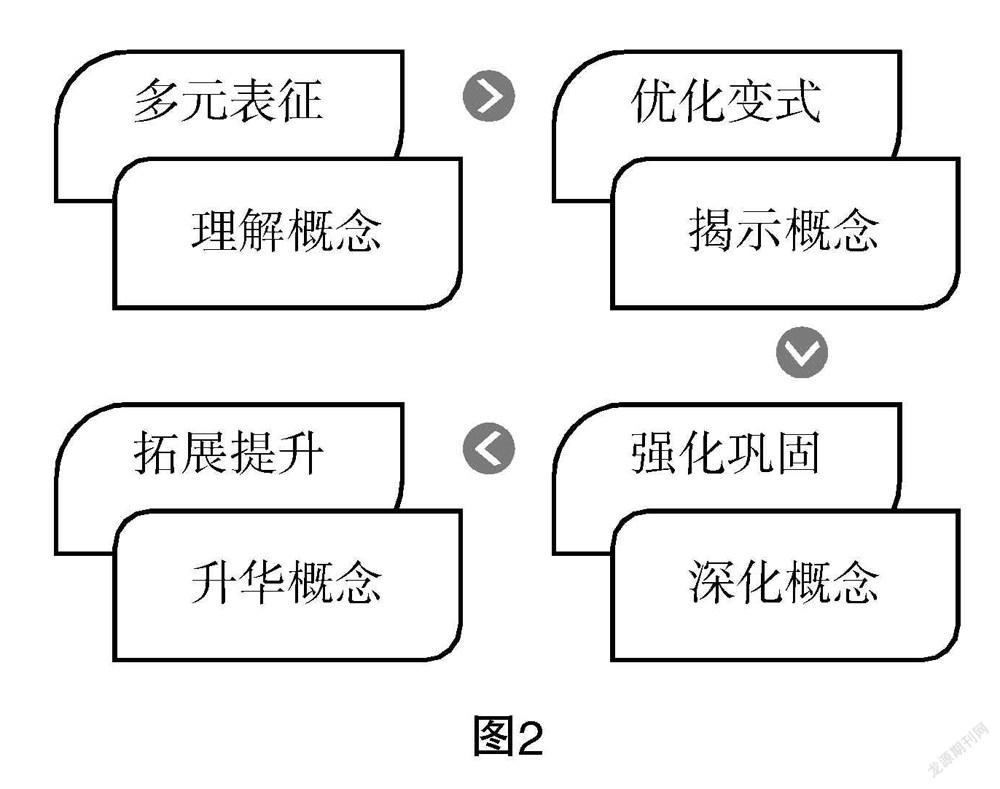
（1）多元表征，深度理解概念、内化核心素养. G·波利亚曾经说过：“学习任何东西，最好的途径是自己去发现，因为这种发现理解最深，也最容易掌握内在的规律和联系.”创设教学情境，帮助学生探究概念的起源及发展、挖掘概念的多元表征、构建概念的认知结构，多元联系、多维比较，促进学生深度理解圆锥曲线的概念，为数学运算提供优良的中枢端，内化核心素养.

案例1：多元表征视角下的两道高考试题.

题1：（2015年浙江省高考数学文科第7题）如图4所示，斜线段ΑΒ与平面α所成的角为60°，B为斜足，平面α上的动点P满足∠PAB=30°，则点P的轨迹是（  ）

A. 直线 B. 抛物线

C. 椭圆 D. 双曲线的一支

题2：（2008年浙江省高考数学理科第10题）如图5所示，AB是平面α的斜线段，A为斜足. 若点P在平面α内运动，使得△ABP的面积为定值，则动点P的轨迹是（  ）

A. 圆B. 椭圆

C. 一条直线 D. 两条平行直线

（2）优化变式，揭示概念本质、内化核心素养.许多运算错误是由于对概念的理解有偏差：理解不全的概念、模糊近似的概念、张冠李戴的概念等. 这就需要优化概念的变式教学、揭示概念的本质，在对比优化中帮助学生理清概念的内涵与外延，为在运算中准确应用概念扫清障碍.

案例2：椭圆与双曲线本质的差异.

题3：如图6所示，圆O的半径为定长r，P是圆上任意一点，A是圆O内一定点，线段AP的垂直平分线l和半径OP相交于点Q，当点P在圆上运动时，点Q的轨迹是什么？为什么？

变式：如图7所示，A是圆O外一定点（注：其他条件与题3相同），点Q的轨迹是什么？为什么？

（3）强化巩固，深化概念应用，发展核心素养. 设计与概念有关的微专题，强化概念的应用，体会圆锥曲线概念的内涵与外延，体验在遇到不同问题的情境下巧妙回归定义、规避复杂的运算，从而达到事半功倍的愉悦心理状态. 在感悟与体验中提升运算能力、发展核心素养.

（4）拓展提升，升华概念精髓，发展核心素养.日本数学教育家米山国藏说过：“在学校所学到的数学知识，在进入社会后不到一年两年就忘掉了. 然而，不管他们从事什么工作，唯有深深铭刻于头脑中的数学精神和数学思想方法却长期地在他们生活和工作中发挥着作用.”数学概念是思想方法的發源地，在教学中要提炼蕴含于概念中的思想方法，升华概念精髓. 在拓展训练中将知识内化，提升运算的思维品质，培育创新能力、发展核心素养.

案例3：巧借类比思想，升华概念精髓.

G·波利亚说过：“类比是一个伟大的引路人.”在数学教学与研究中，类比是进行合情推理的一种非常重要的思维方法. 高中数学新课程已经将“类比推理”能力的培养作为了课程目标之一，在近几年的高考中也大量出现了能力立意，“多一点想，少一点算”的类比题. 圆与椭圆是两类重要的有心二次曲线，圆的很多性质及与其相应的解题方法可以与圆锥曲线类比.

题4：（2012年浙江省高考数学理科第21题）如图9所示，椭圆C：+=1（a>b>0）的离心率为，其左焦点到点P（2，1）的距离为，不过原点O的直线l与C相交于A，B两点，且线段AB被直线OP平分.（1）求椭圆C的方程;（2）求△ABP面积取最大值时直线l的方程.

题5：（2013年浙江省高考数学理科第21题）如图10所示，点P（0，-1）是椭圆C：+=1（a>b>0）的一个顶点，C的长轴是圆C：x2+y2=4的直径.l，l是过点P且互相垂直的两条直线，其中l交圆C于A，B两点，l交椭圆C于另一点D. （1）求椭圆C的方程;（2）求△ABD面积取最大值时直线l的方程.

题6：（2014年浙江省高考数学理科第21题第（1）问）如图11所示，设椭圆C：+=1（a>b>0），动直线l与椭圆C只有一个公共点P，且点P在第一象限. 已知直线l的斜率为k，用a，b，k表示点P的坐标.

2. 优化策略，指明运算方向、促进深度思考

“人的一生，是一连串决定交织而成的过程，其精华在于自己如何选择. 生命的最高境界，就是选对舞台，尽情挥洒才华，走出自己的路. ”所以解决问题需要最优的解法，“方法大于苦干”. 浙江省高考数学的命题特点为：能力立意，“多一点想、少一点算”. 所以选择运算策略显得尤为重要. 笔者对2014年至2020年共七年全国各地关于圆锥曲线的高考题进行了分析，并结合浙江省高考数学的命题特点及其教学实践，提炼了圆锥曲线优化运算的6种常用策略（见图12），在解题中可以穿插运用，帮助学生指明运算方向、优化运算方法，在对比优化中促进深度思考、发展核心素养.

策略.

题7：已知点A（x1，y1），B（x2，y2）是抛物线y2=4x上相异两点，且满足x1+x2=2.  （1）若AB的中垂线经过点P（0，2），求直线AB的方程;（2）若AB的中垂线交x轴于点M，求△AMB面积的最大值及此时直线AB的方程.

（1）对比多元运算方法，优化选择意识：

（2）反思算法，形成策略，提升运算能力：

3. 强化运算，提升运算速度、促进深度参与

设计有效的强化运算的方案，强化运算体验，积累运算经验，帮助学生熟练掌握运算——做到算理熟练、算式规范、算法简捷、结果准确.

（1）微专题式强化：精准施教，点点击破（见图13）. 关注学情与考情：圆锥曲线命题的热点与难点，学生运算的困难点与再生点;以此为素材构建微专题，利用微专题实施精准的教学，突破运算障碍.

案例5：弦长计算类微专题的设计点.

设计点1：弦长公式优选问题：普通弦长;焦点弦;通径.

设计点2：弦长的取值范围问题.

设计点3：巧借弦长转化的综合问题.

（2）微说题式强化：思维可视化. “说”源于“思”，训练数学思维的最优方法是“说题”. 在精心做题的基础上，展示运算方式、解题策略和推理依据，凸显思维可视化，并通过归纳、概括，总结出经验性运算策略. 在运算教学中把学生引入“说题”，交流运算困惑、分享运算心得，有利于提升运算能力，培养创新思维能力、发展核心素养. 见图14.

（3）微检测式强化：提升效率.微检测是指立足学情、教情、考情，针对近期（时间间隔不超过一周）讲过的运算类易错题的专题性的巩固与检测. 考试题量在10道题以内，时间在合适范围以内;出题者可以是教师，也可以是学生. 通过微检测帮助学生发现运算障碍，优化运算方案、提升运算速度.

4. 错中反思，巩固运算经验、促进深度感悟

荷兰著名的数学教育家弗赖登塔尔指出：“反思是数学思维活动的核心和动力.”美国教育家杜威指出：“真正思考的人从自己的错误中吸取的知识比从自己成就中吸取的知识更多，错误与探索相联姻、相交合，才能孕育出真理.”运算错误是运算能力提升的生长点，要引导学生在错误中反思，透析错误背后所蕴含的价值，加以研究、开发与利用. 在错误中感悟运算真谛，在感悟中巩固运算经验、提升运算能力. 见图15.

（1）知识层面类反思，弥补知识漏洞、加固运算根基. 教师与学生“个体反思+集体反思”：反思教与学，优化教与学，提升教学效益，为数学运算提供充足的养分. 对知识纵向反思、横向反思，挖掘知识的内涵与外延，构建知识网络，加固运算根基.

（2）思想方法类反思，优化运算策略、提升运算效益.数学思想是解决数学问题的指路灯，是运算灵感的发源地！挖掘运算错误背后的思想根源，揭示运算本质. 通过“一题多思”“多题对比”感悟思想、优化策略，提升运算效益.

案例6：数学思想指导下的“一题多解”的运算反思.

题8：（2014年江西省高考数学理科第15题）过点M（1，1）作斜率为-的直线与椭圆C：+=1（a>b>0）相交于点A，B. 若M是线段AB的中点，则椭圆C的离心率为__________.

目标反思：圆锥曲线的离心率，是描述曲线形状的重要参数，很多的圆锥曲线试题都与此相关，在历年的高考试题中频繁出现. 解决此类问题，需要认真审核，利用题目信息、所给的数式与图形，构造关于a，b，c三个量的等量关系或不等关系，从而找到解题方向.

解法反思：三種思想指导下的三类不同解法. （具体略）

优化反思，形成策略：点差法是处理中点弦问题的最佳策略！！

（3）经验成果化，借鉴运算经验、分享运算心得.美国哈佛大学校长普西曾经深刻地指出：“一个人是否具有创新能力，是‘一流人才和三流人才之间的分水岭.”将运算类“三微”（见图16）作为课堂教学的延伸、拓展与补充，能够多方面地弥补课堂的不足. 设计一些适应不同层次的学生拓展、延伸的微课，这不仅是课堂教学的延伸，也是激发学生学习兴趣的方法、深化教学内容的过程. 使用微课，能激起学生的思维涟漪，通过比较分析、实践反思、微写作等教学活动促进学生深度思考，在思考中感悟，在感悟中提升.

案例7： 学生习作《“1”与椭圆的奇妙情缘》.

“1”是数字王国中一个奇特的“人物”，他的地位无人可以取代，他的作用无人能及. 他在求最值中有着奇妙的应用.

“1”的奇妙运算：“1”具有奇妙的恒等运算性质“1×a=a（a∈R）”，这为我们求最值时进行恒等变换起到了很大的作用.

例如，已知+=1，求3x+2y的最小值.

解：3x+2y≥（3x+2y）

+

=13++≥13+2=25. 当且仅当=，即x=y=5时取等号.

“1”的奇妙变换：在三角函数中，sinα与cosα有着不变的关系，即“sin2α+cos2α=1”，这为“1”提供了一个奇妙的身份，在求最值时能发挥重要作用.

例如，已知+y2=1，求3x+2y的最小值.

解：因为+y2=1，令

=sinα，

y=cosα，所以3x+2y=6sinα+2cosα=2sin（α+β），所以-2≤3x+2y≤2.

小结：若遇到条件中有平方和为常数的求最值的问题，则可以使用换元法.

教育的目的是什么？怀特海指出：“教育的对象是有血有肉的人，教育的目的应在于激发和引导学生的自我发展之路.”以数学运算为载体，促进深度学习是实现学生自我发展的有效途径，也是每位教师值得研究的课题！