在初中数学教学中用“另类”行为让知识点植入无痕

林锦莺

[摘  要] 在教材的基础上，通过深入挖掘教材本质，通过某种“另类”行为，能让学生自行深入数学世界，体会数学学习的乐趣，感受数学的魅力. 而这个“另类”行为在实施过程中充分地将数学抽象性、逻辑性、理论性的知识演变成学生看得到、听得到、说得出、感受得到的直观结果.

[关键词] 数学教学;另类;知识点;植入

“另类”这个词语可以是与众不同的意思，也可以说是背离主流行为的意思. 不可否认在数学教学中有很多常规传统行为，为学生的数学学习立下了汗马功劳，但是我们应该更进一步思考，是否可以在教材的基础上，通过深入挖掘教材本质，通过某种“另类”行为，让学生自行深入数学世界，体会数学学习的乐趣，感受数学的魅力. 而这个“另类”行为在实施过程中充分地将数学抽象性、逻辑性、理论性的知识演变成学生看得到、听得到、说得出、感受得到的直观结果.

因此，如果教师能够突破常规，创造出一些“另类”行为，帮助初中生了解所学知识，特别是突破知识难点，让知识点呈现更加直观，在教学中植入无痕，我们就不能拒绝这样的“另类”行为. 下面就几个“另类”行为进行举例说明.

用折纸动态演示数学原理

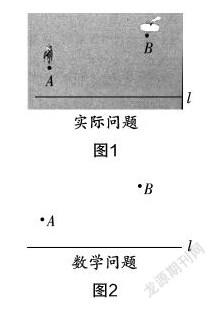
“最短路径问题”是初中义务教育阶段重要的课题学习内容. 我们来看一道数学经典名题“牧马人饮马”：如图1，牧马人从A地出发，到一条笔直的河边l饮马，然后再到B地，牧马人到河边的什么地方饮马，可使所走的路径最短？

这个生活实际问题经过提炼建立数学模型后，其实是两点在直线同一侧的时候，在直线上找一点到两点距离之和最小的问题. 教师一般会引导学生想到利用轴对称原理将问题化为两点在直线异侧情况，从而利用“两点之间线段最短”公理来得到问题的解决方案.

但是往往在这个过程中，大部分学生总觉得很抽象，很难想出具体的解决方案. 教师作为分析问题的引导者，如何让学生进行充分思考、合情推理，进而联想到利用轴对称相关知识将问题转化为已知模型是关键. 笔者认为可以将模型在一张A4纸上呈现，如图3，学生在纸上能更加直观清晰地看到问题本质，再结合小时候的折纸经验，激发学生强烈的动手欲望，就很容易找到解决问题的方案. 学生将纸张部分对折变成两点异侧模型，如图4、图5，从而获得突破难点的解题体验. 在这个过程中，两点同侧是基本模型，考查的只是“两点之间线段最短”，两点异侧模型只要叠加上轴对称知识就可以得到转化与解决. 因此，学生折纸这个有形动作使其很自然地联想到轴对称的知识，从而将问题完美过渡到两点同侧的基本模型.

常规的路径之和最短问题的教学中，大部分教师都采用启发式教学，但在启发过程中部分教师还是会出现一瞬间抛出“轴对称”相关知识的情况. 因此我们需要慢下来，做个改变，可以给学生足够的时间，比如本节课重点让学生在一张白纸上画一画、折一折、叠一叠、看一看，使其在眼睛、双手、大脑的全面结合中，在充分渗透数学思维的行为中找到解决途径，同时把轴对称知识的应用无痕地植入了学生的大脑. 相信这个参与行为会让学生学习数学的积极性有质的飞跃.

让流行音乐进入数学课堂

初中生对新鲜事物常常表现出强烈的好奇心，如果教师能够在常规的数学课堂中加入学生喜欢的元素，比如流行音乐，在提升教学效果上将起到事半功倍的作用. 比如在“代入法解二元一次方程组”（人教版七年级下册）的教学中，笔者为了提高学生学习的热情，在课堂总结的时候，按照当年流行的歌曲《野狼disco》编了一首《代入法disco》，歌词如图6所示.

用代入法解二元一次方程组，不是对数学问题进行正面击破，而是侧面转化. 这种代入转化思想在学生后续的学习中会经常遇到，学生后面还会学习整体代入转化思想，这在一些方程组求解和代数式计算中都是非常重要的思路. 因此，在这个节骨眼，我们要慢下来，研究如何让学生对代入转化思想有深刻记忆. 实际教学时，在歌声的聆听与哼唱中，学生对代入消元法产生了巨大的兴趣，对其有了深刻的记忆和理解. 这首歌起了桥梁的作用，帮助学生从会解决单一的一元一次方程过渡到能够解决二元一次方程组，这个知识点的升华虽然无痕，但是记忆有痕.

用站位体现整数点

《数学课程标准》中指出：数学教学是数学活动的教学，是师生交往互动以及共同发展的过程. 在初中生的数学学习中，特别是在一些较难或易错知识点的学习中，教师应想方设法创造性地加入一些“另类”活动帮助学生理解知识点，让学生在活动中形成深刻记忆，固化正确认识，加强学生对概念的认识与掌握.

七年级学生在学习绝对值这一章节的时候，常常对绝对值的概念理解不是特别透彻，导致解题时生搬硬套，造成错解、漏解. 例如这道填空题：当x=2时，x=______;当x-1=2时，x=______;当x+1=2时，x=______. 可以预见学生在做题时很容易漏解、错解. 这时我们可以选派若干学生来讲台站成一排，如圖7.

选定某人为原点，其他人左右依次排开为整数点，这时候学生从绝对值定义出发，看人识数，很容易意识到x=2的x代表到原点距离为2的人有两个，所对应的数也有两个，即±2. x-1=2的x代表到1距离为2的人有两个，所对应的数为3和-1. x+1=2的x代表到-1距离为2的人有两个，所对应的数为-3和1. 在这个站位活动中学生能够看人说数，形象直观，这种活动刺激比一遍又一遍强调概念更加有效，很好地突破了绝对值概念理解上的难点.

教师在教学中能选用的教学手段千千万万，但是教师要努力确保学生能力的养成和提升，就可以多挖掘类似于“站位体现整数点”的活动让知识难点呈现得更加直观丰满，使学生的知识内化更加深入.

就地取材举例子

大部分初中生还是以直观思维作为思考的起点，所以对于教学的某些知识难点教师可以采用直观模型演示的方式对其进行呈现，让学生基于现有材料就地取材，科学地发现思维通路，主动发现问题所在，从而掌握一个知识难点，获得对数学知识的深层认知.

比如我们知道“两个三角形若满足两条边相等和其中一条边的对角相等，这两个三角形不一定全等”，但这个命题对学生来讲比较抽象、生涩，难以理解. 这时候教师可以让学生拿出笔或直尺，摆出满足以上条件但不全等的两个三角形，学生在动手操作过程中会产生强烈的求知欲以及一定要成功的愿望. 学生在同桌或小组的合作探究中摆出了如图8的模型，完成了任务. 在这个过程中学生摆脱了机械记忆知识难点的方式，用现成的材料实现了对知识难点的突破，培养了学生“自主发展”的核心素养.

用魔术还原数学概念

兴趣对学生学习有着积极的影响是教师们的共识. 教师应该从兴趣出发，积极寻找能让学生或参与，或观察，或配合的活动，让学生在自主探究活动中自然深入课堂，进入学习状态. 比如教学“中心对称图形”这一章节时，教师可以引入魔术活动，在充分吸引学生注意力的基础上，让学生尽快进入学习新知的状态，为深刻理解概念做好铺垫.

教师先抛出一个魔术：如图9，教师背对学生，随机指定某位学生在五张扑克牌中任选一张，绕牌的中心点进行180°旋转，然后教师能快速找出被旋转的是哪张扑克牌. 这个活动与其说是魔术，不如说是中心对称图形的一个应用活动. 我们知道扑克牌中的“梅花10”是中心对称图形，如果学生将這张牌旋转180°，则图形完全没有改变，但是学生旋转其他四张牌中的任何一张，因为它们不是中心对称图形，就很容易识别哪一张牌发生了变化. 这个活动大大激起了学生探究中心对称图形的兴趣. 魔术过程中学生恍然大悟，这个“悟”能够很自然地引入新知，因此学生在魔术活动中直观清晰又毫无痕迹地了解了“中心对称”的概念，对知识的掌握也从感性认知上升到理性认知.

2014年，教育部发布了《关于全面深化课程改革，落实立德树人根本任务的意见》，其明确提出将研究制定各学段学生发展核心素养体系. 初中数学内容知识点较多，其中体现出来的核心素养有：数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析. 为培养学生的核心素养，教师可以将学生的形象思维作为思路点拨的起点，并且在实际教学中帮助学生找到问题条件和答案之间的联系，把题目变得清晰明朗，让学生准确分析出解决问题的途径和方法. 这样的教学能实现技能叠加，突破知识难点，让知识点无痕植入. 在教师的这些“另类”行为中，学生的思维活动是充分的，并且学会了用数学的思维观察事物、解释现象，从而解决问题，同时培养了学生的数学核心素养.

相对于知识本身，学生获取知识的过程更重要，如果说“知其然”是知识，那么“知其所以然”才是智慧. 伴随着社会的高速发展和教育改革的深入，初中数学教学不能满足于现状，教师应该在初中数学教学中用创造性的“另类”行为让知识点无痕植入，开拓学生思维，培养学生的数学核心素养，提高学生在未来的竞争力，从而实现其自我价值.

3759501908266