放缩法证明数列不等式的策略探究
甘肃省兰州市第六中学(730060) 焦永垚
数列不等式的证明是高中数学中的重点和难点,是历年高中各类考试中的热门考点,这类问题通常难度较大,具有很高的综合性与灵活性.本文以2019年全国高中数学联赛贵州省预赛试题(B)卷第16 题为例,从不同角度探寻放缩法证明数列不等式的策略与方法,重点阐述如何选择合理地放缩思路,如何准确把握放缩的“尺度”,以期能帮助同学们从根本上认识放缩法的规律,从而优化解题方法,提升解题能力,提高解题效率.
一、试题分析
题目设数列{an}的前n项和Sn满足:Sn=k·qn−k,其中k,q为非零常数,且a1=3,a4=81.
(1)求数列{an}的通项公式;
(2)设bn=an −证明:
分析第(1)问考查数列的基础知识,易求得an= 3n.第(2)问是数列不等式的证明,数学归纳法是解决这类问题的优选方案.
当n=1 时,不等式成立.
假设当n=k(k ∈N∗) 时结论成立, 即那么当n=k+1 时, 因为bn −3bn−1=>0, 所以bn >3bn−1, 即(n≥2), 则即当n=k+1 时不等式也成立.
综上,对于一切正整数n,不等式都成立.
可以看到,上述方法中我们需要克服以下三个难点:
(1)如何利用归纳假设?
要证明当n=k+1 时结论也成立,如何利用归纳假设,是解决问题的的关键, 为了利用假设, 我们需要找出与的关系, 要找出的等量关系难度太大,所以考虑它们的不等关系,也就是放缩.
(2)怎样放缩?
因为bn= 3n −容易发现{bn}为递增数列,所以(n≥2), 因此我们会首先做这样的尝试: 当n=k+ 1 时,放缩过度了.
(3)如何调整放缩度?
经历(2)的尝试,发现放缩过度了,需要调整放缩的度:如果忽略bn= 3n −中的则有bn= 3bn−1(n≥2),于是我们猜想bn >3bn−1,是否成立呢? 因为bn −3bn−1=>0,所以bn >3bn−1,可得(n≥2),再进行计算发现刚刚好.
从以上过程可以看到,放缩法是证明数列不等式的重点和难点,因此我们有必要进一步探究放缩法证明数列不等式的思路与策略.
二、思路探究
思路1放缩成一个等比数列
策略1利用不等式放缩,其中a >b >0.因为于是,当n=1 时,不等式成立;当n≥2 时,

综上,对于一切n ∈N∗,都有
点评在证明数列不等式的问题中, 对于形如(a >b >0) 的数列,通常可以利用不等式将其放缩为一个等比数列.
策略2利用不等式3n≥2·3n−1+ 1 放缩.因为3n −2·3n−1= 3n−1≥1, 所以, 对任意n ∈N∗, 都有3n≥2·3n−1+1 成立.所以,于是, 当n= 1 时,当n= 3 时,当n≥4 时,

综上,对于一切n ∈N∗,都有
点评此证法中如果只保留第一项,从第二项开始放大,则放缩过度了;如果保留前两项,从第三项放大,则<依然太大了,只有保留前三项,从第四项开始放大,才能得到符合的结果.因此,当出现放缩过度的情况时,就要适时进行“局部调整”,保持前若干项不变,从后面的项开始放缩,反复尝试,直至成功.
思路2向裂项相消放缩
宫颈成熟能够提高顺利分娩的几率,近来常用的促进宫颈成熟的方法有乳房按摩方法[6]。本篇文章设置对比实验,对照组使用常规孕产妇检查方法,实验组在常规方法基础上使用乳房按摩方法。实验结果说明实验组孕产妇的宫颈评分以及总有效率,远远高于对照组,说明乳房按摩能够促进宫颈成熟。
策略1放缩成的形式,λ为常数.当n≥2 时,
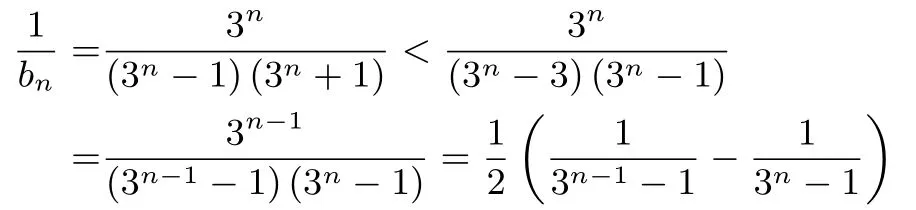
所以,当n= 1 时,; 当n= 2 时,当n≥3 时,
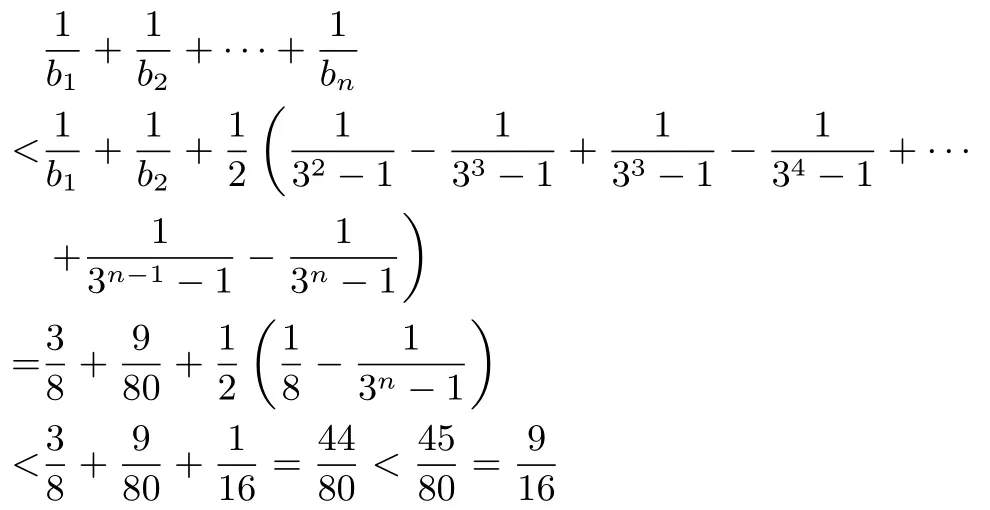
综上,对于一切正整数n,都有
策略2放缩成
的形式,λ为常数.因为为了便于用裂项相消法求和, 所以我们联想能否把中的全部或者部分项放大成的形式.我们先逆向进行探索, 因为所以要使, 只需只需只需3n+3<2·3n −2, 即3n >5, 显然当n≥2 时成立, 所以, 当n≥2 时, 有于是当n= 1 时,当n= 2 时,当n= 3 时,当n≥4 时,
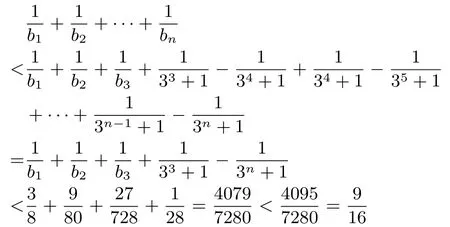
综上,对于一切正整数n,都有
思路3利用“糖水不等式”放缩
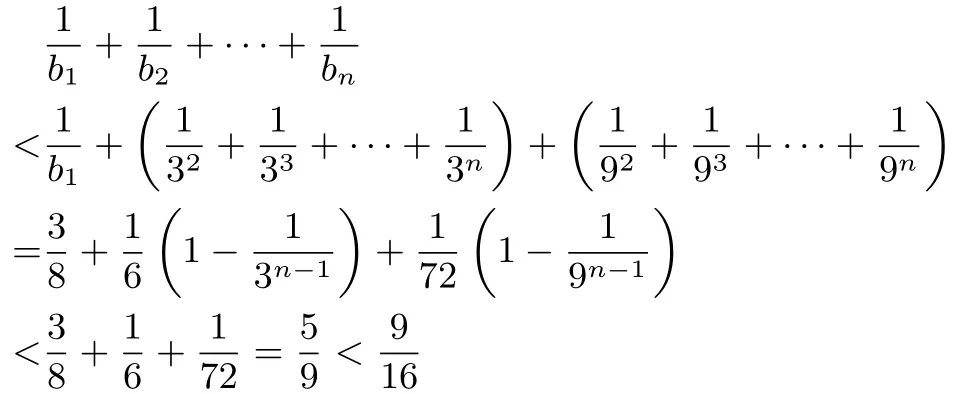
综上,对于一切正整数n,都有
思路4利用分项比较法放缩
策略1执果索因, 逆推探源.不等式的左边是数列的前n项和, 右边为一个常数, 结合的结构, 我们联想, 把右边常数缩小成某个等比数列{cn}的前n项和, 然后只需证明≤ck就可以了, 其中k= 1,2,···n.那么{cn}究竟等于什么呢? 我们可以逆推回去: 要证成立, 只需证成立, 设数列{cn}的前n项和Tn=则当n≥ 2 时,cn=Tn −Tn−1=,当n=1 时,c1=T1=符合上式,故cn=.于是,由≤0 可得≤ck, 其中k= 1,2,···n, 所以即
策略2逆用累加法.同思路4, 先把常数缩小为即要证,只需证
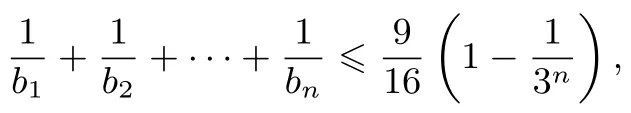
而
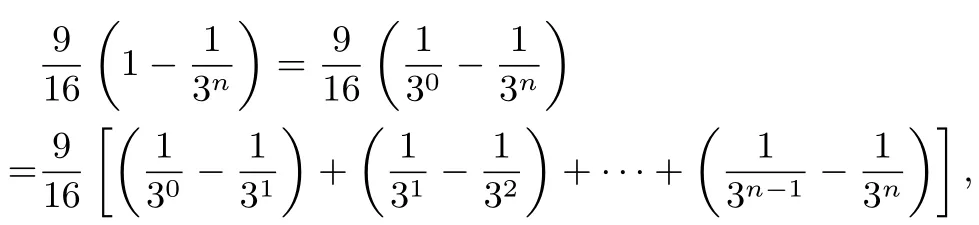
三、小结反思
数学归纳法和放缩法都是证明数列不等式的常用方法,而放缩法通常学生感觉无从下手,不知所措,主要表现在以下几个方面:
(1)用什么方法放缩? 首先要搞清楚到底是放大还是缩小,再考虑采用哪种放缩方法.常见的方法有利用均值不等式、“糖水”不等式、放大(或缩小)分子(或分母)、一些常用的不等式等等.
(2)向什么方向放缩? 对于像母题中与数列前n项和有关的不等式,放缩的原则是经过放缩后能够求和,比如放缩成一个等比数列、向裂项相消放缩等等.
(3)如何把握放缩的度? 我们经常会遇到放得“太大”或“太小”的问题,这就要求调整放缩的尺度,例如在本文中,当我们发现放缩得“太大”时,就要采取补救措施,即保留前若干项不变,对后面的项进行放缩,逐一尝试,直至成功.
另外,本文中的这道竞赛题是一道典型而设置巧妙的考题,它之所以能引起我们强烈的共鸣与反响,不仅仅是因为其独特的解题思路与技巧,更是因为问题中所蕴含的丰富的数学知识思维和思想方法.这样的题目有利于学生模式化解题的总结,不仅仅教会了学生怎样解题,而且还有效地培养了学生思维的广阔性和灵活性,提高了解题效率.

