待定系数法结合均值不等式解决多元条件极值问题

北京大学附属中学(100190) 单治超

均值不等式是高中数学的重要内容, 其内容容易理解,但是具体运用时则灵活多变.国家课标对均值不等式的要求难度并不高.但是2020年的北大和复旦强基计划数学试题都考查了利用待定系数法结合均值不等式解决给定条件下多元函数的最值问题.我们又注意到前两年的清华领军计划也都考查了类似的题目.这类题目的频繁出现,使得准备强基计划的同学必须引起高度重视.为此,我们撰写本文对这种方法进行一点梳理.

我们用到的工具很简单:

定理1(具有待定系数的二元均值不等式) 对任意C ＞0,x ＞0,y ＞0,当且仅当y=C2x时取等号.

证明显然.

例1(2020年北大强基计划第9 题) 求使得5x+12>xy≤a(x+y) 对所有正实数x,y都成立的实数的最小值a.

解易见这个最小值就是二元函数f(x,y) =在条件x ＞0,y ＞0 下的最大值.对任意C ＞0,

为了让不等式的右端除以x+y是个定值, 我们令5 + 6C=即C=此时我们得到f(x,y) ≤9.很容易验证等号可以取到.所以f(x,y) =在条件x ＞0,y ＞0 下的最大值是9.因此a的最小值是9.

从这个例题我们领会到, 利用待定系数的均值不等式,关键点在于令待定的系数能够使得两个式子的比例为定值.

我们再做一道例题巩固对这种方法的理解.

例2(2020年复旦强基计划第2 题)已知实数x,y满足x2+2xy −1=0,求x2+y2的最小值.

解对任意C ＞0,

为了令不等式的右端与x2+y2的比例为定值, 我们令1+C=即C=于是x2+y2≥容易验证等号可以取到,所以x2+y2的最小值是

前面两个例子都是2020年强基计划的试题.事实上,这种方法在以往的清华领军计划试题中已经有所考查.

例3(2018年清华领军计划第10 题)设a,b,c为正数,且a2+b2+c2=1,求a(a+b+c)的最大值.

分析这道例题相对前两道例题的难度在于出现了三个变量,但是容易发现b,c两个变量的地位是相同的,因此我们在利用均值不等式对只涉及b,c的解析式进行放缩时,不需要利用待定系数的均值不等式.

解对任意k ＞0,

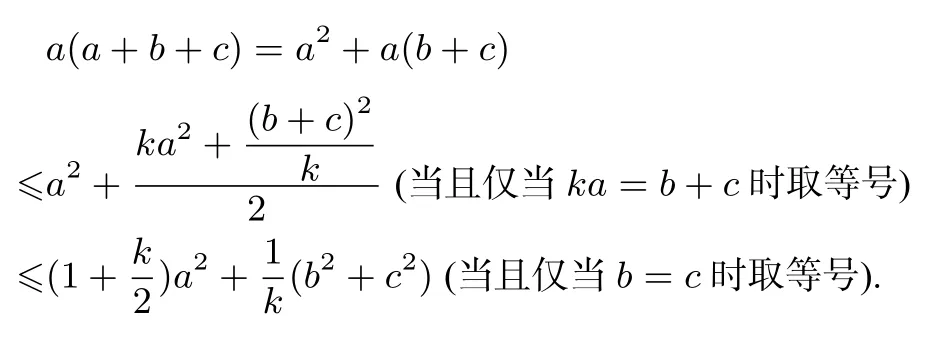
为了令不等式的右端与a2+b2+c2的比例为定值,我们令于是

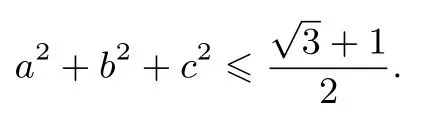
容易验证等号可以取,所以a(a+b+c)的最大值是

2019年清华领军计划还出过一道更难的题,需要利用待定系数的三元均值不等式.

定理2(具有待定系数的三元均值不等式) 对任意k ＞0,l ＞0,x ＞0,y ＞0,z ＞0,当且仅当kx=ly=z时取等号.

证明显然.

例4(2019年清华领军计划第23 题)已知ab(a+8b)=20,求a+3b的最小值.

解对任意正实数k,l,

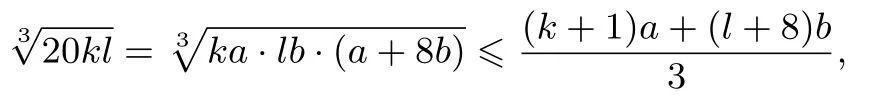
为了令不等式的右边与a+3b的比例是定值,我们需要令

注意到满足这个等式的正有序实数对(k,l)具有无数个,但是仅满足这个等式的(k,l)不足以让我们达到目的,因为此时我们必须考虑不等式取等号的条件ka=lb=a+8b能否实现.容易发现,这个条件能够实现当且仅当

联立方程组(1)(2),它的正实数对解只有一个:k=5,l=10.于是可求得a+3b的最小值是5.

我们运用例4 的方法,可以对例4 的结论一般化:

定理3设p,q是给定的正常数,在已知ab(a+pb)=1,a,b ＞0 的条件下,a+qb的最小值是其中

证明对任意正实数k,l,

为了令不等式的右边与a+qb的比例是定值,我们需要令

不等式取等号的条件是ka=lb=a+pb.这个条件能够实现当且仅当

联立方程组(1) (2), 它的正实数对解只有一个:k0=因此我们就得到了想要的结论.