一道最大值高考模拟题的探究

湖南省会同县第一中学(418300) 于先金 杨 瑜

一、试题呈现,简洁对称

题目(江苏省镇江市2018 届高三上学期期末(一模)统考试题第13 题)设a,b ∈R,且a+b=4,则的最大值为____.

这道试题简洁、对称、优美,设有陷阱并有一定难度,主要考查转化化归思想与运算能力, 考查基本不等式的应用,考查的核心素养是逻辑推理和数学运算.

二、几点疑问,引发探究

不少学生一拿到这道题,认为这还不简单,这是一道填空题,只要结果不要过程,根据题设条件和目标式的对称性,显然应该当a=b=2 时,y=取得最大值,所以所要求的最大值为

答案错了! 错在哪里?

对这道模拟题,各种资料和网上都这样写道: 本题考查的内容是基本不等式,是一道原创题,考查的技能和能力是转化化归思想与运算能力,答案是遗憾的是都没有给出详细的解答过程,也许是解答过程过于简单的缘故.

三、解法探究,殊途同归

解法1(化归一元,不等放缩)

因为a+b=4,所以可将目标式通分化简

因为a+b= 4,所以16 = (a+b)2=a2+b2+2ab≥2ab+2ab= 4ab,所以ab≤4.令x= 9−ab,所以x≥5,当且仅当x=即x=时等号成立.所以的得最大值为

这种解法也许是命题人所希望的解法,真正体现了转化化归思想,考查了学生的运算能力,考查的数学核心素养是逻辑推理和数学运算.

解法2(导数登台,单调唱戏)

由解法1 得y=及ab≤4,令x=ab,则y=f(x)=其中x ∈(−∞,4].易求得从而f(x) 在区间(−∞,9−上单调递增, 在区间上单调递减,则所以的得最大值为由上可知,当x →−∞时,f(x)→0,所以y的取值范围是

利用函数的单调性来解最值问题,对函数值的变化情况就一目了然了.

解法3(均值换元,判别式法)

因为a+b=4,令a=2−t,b=2+t,所以y=令t2+ 5 =x, 所以x≥ 5,y=即yx2−(16y+ 2)x+ 80y= 0.因为y ＞0,x≥5, 所以∆= (16y+2)2−320y2≥0, 即16y2−16y −1 ≤0, 解得0＜y≤又当x=时,y=所以的得最大值为

四、推广探究,开拓视野

推广1 设a,b ∈R, 且a+b= 4, 0＜k≤12, 则的最大值为

证明(换元化归,不等式法)

因为a+b= 4,所以a2+b2= 16−2ab,且ab≤4,令于是

令x=k+8−ab≥k+4,所以ab=k+8−x≤4.所以

y≤当且仅当x=即x=时等号成立.因为0＜k≤12, 所以≥k+ 4 成立.所以的最大值为

推广2设a,b ∈R, 且a+b= 2m,m≥则的最大值为

更一般地,我们有:

推广3设a,b ∈R,且a+b= 2m,3m2≥k ＞0,则的最大值为

类似于推广1 的证明,不难证明推广2、3,证明略.

推广4设a,b ∈R,且a+b=4,则的最大值为

证明(换元化归,利用单调)

因为a+b=4,易求得a3+b3=4(16−3ab),且ab≤4.令y=易求得y=令x=ab, 则y=f(x) =其中x ∈(−∞,4].易求得f′(x) ==从而f(x) 在区间(−∞,4−上单调递减,在区间

对于如下问题,有兴趣的读者可作进一步探究:

问题1若正数a,b满足a+b= 4, 求(n ∈N,n≥4)的最大值.

问题2若正数设a,b,c满足a+b+c= 4, 求的最大值.

问题3设正实数a1,a2,··· ,an(n ∈N,n≥3) 满足a1+a2+···+an=4,求的最大值.

五、变式探究,精彩纷呈

变式1已知正数a,b满足a+b=4,则的最大值为

变式2已知正数a,b满足a+b=4,则的最大值为

类似于原模拟题的解法,不难证明变式1、2,证明略.

变式3已知正数a,b满足a+b=1,则的最大值为

证明(代入消元,一步到位)

因为正数a,b满足a+b=1,所以b=1−a.所以

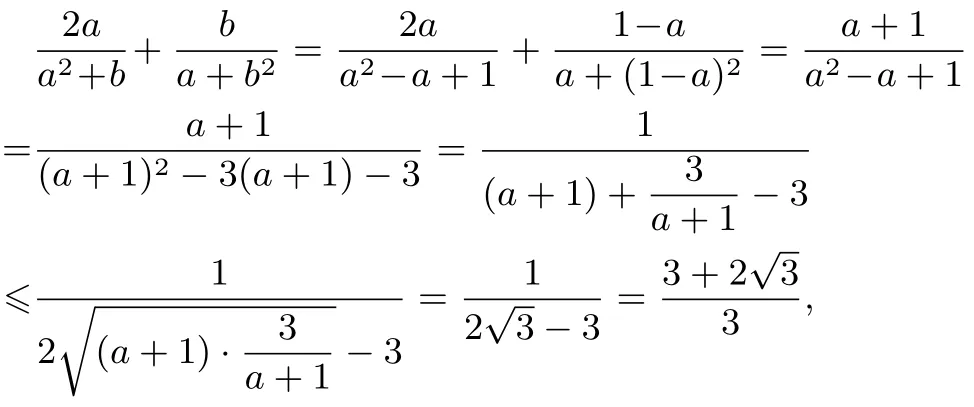
当且仅当a+1=即时等号成立.所以的最大值为

变式4已知正数a,b满足a+b=4,则的最大值为

类似于变式3 的证明,不难证明变式4,证明略.

变式5已知正数a,b,m,n, 且a+b= 4, 则的最小值为

由柯西不等式可知,结论显然成立,证明略.

变式6已知正数a,b满足a+b=4,则的最小值为

证明(利用原解,函数性质)

由原题的解法2 得y=f(x) =x ∈(0,4],f(x) 在区间(0,9−√上单调递增, 在区间上单调递减,又f(0)=所以f(x)的最小值为所以的得最小值为

变式7已知正数a,b满足a+b=4,则的最小值为

变式8设正实数a1,a2,··· ,an满足a1+a2+···+an=nr,m ＞1,0＜k ＜则的最小值为

证明(加权凹凸,化难为易)

由加权不等式可得

所以

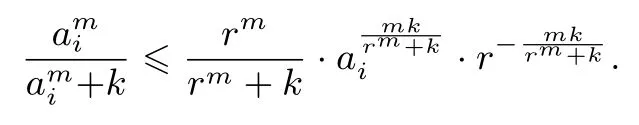
所以

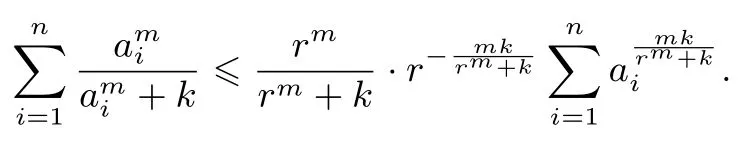
因为m ＞1,0＜k ＜所以0＜＜1,由函数的凹凸可知

所以

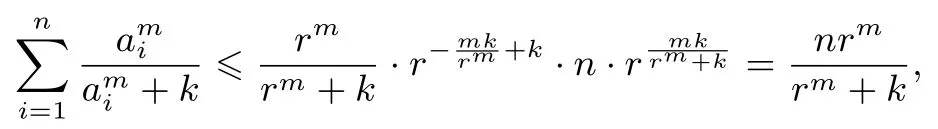
所以

当且仅当a1=a2=···=an=r时等号成立.所以的最小值为

特别地, 如果正数a,b,c满足a+b+c= 4, 则的最小值为(在变式8 中,取n=3,m=2,k=1,r=便可.)

六、一点思考,教学相长

数学是有用的,数学是自然的,数学是清楚的,数学是优美的,数学是好玩的.

在数学教学中,时常会遇到各种各样的问题,这时我们要善于引导学生积极开动脑筋,乐于思考,勤于思考,善于思考,逐步培养学生独立思考的习惯,引导学生进行探究.

探究必须植根于具体问题之中.探究是一个计划、行动、反思,再计划、再行动、再反思的过程.探究不仅是一把金钥匙,帮助我们打开智慧殿堂的大门;探究还是一叶方舟,承载我们到达理想的彼岸.在教学中,要为学生提供微探究的机会,让学生在探究中体会到学习的快乐,体会到“数学好玩”,让探究成为一种习惯.