对一道全国大联考试题的拓展探究
福建省福州市闽侯县第一中学(350100) 黄美琴
各类试题均是命题者集体智慧的结晶,含有丰富的数学内涵,具有可探究性和进一步拓展的空间,值得我们去深入探究.引导学生对一些典型的试题进行分析思考、多角度探究拓展,这对培养和提升学生的创新能力、数学学科核心素养无疑是有益的.正如美国数学家波利亚所说:“一个专心备课的教师能够拿一个有意义的但又不太复杂的题目,去帮助学生发掘问题的各个方面,使得通过这道题,就好像通过一道门户,把学生引进一个完整的理论领域”.下面是通过引导学生对一道全国大联考试题进行的纵向、横向和变式拓展.
题目(2020 届高三全国第一次大联评数学试题(理科) 第19 题)已知抛物线y2= 2x, 过点P(1,1)分别作斜率为k1,k2的抛物线的动弦AB,CD, 如图, 设M,N为线段AB,CD的中点.(1) 略; (2) 若k1+k2= 1, 求证直线MN恒过定点,并求出定点坐标.
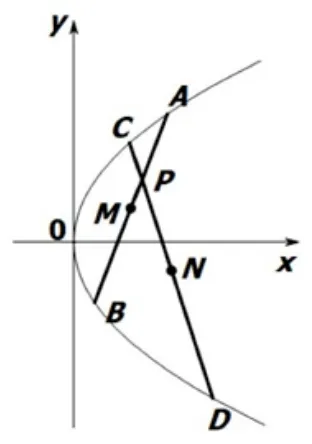
本题(2)的答案是直线MN恒过定点(0,1).本小题内涵丰富,意境深邃,具有拓展空间,值得我们引导学生进行适当的探究拓展.
1 纵向拓展: 由特殊到一般的拓展
对本题(2)的结论, 我们不禁要问: 对于一般的抛物线y2= 2px(p >0),定点P(m,n),k1+k2=λ(λ为常数),直线MN是否恒过某个定点? 经探究,可得
性质1.1已知抛物线y2= 2px(p >0), 过不在抛物线上的定点P(m,n)分别作斜率为k1,k2的抛物线的动弦AB,CD,设M,N为线段AB,CD的中点,若k1+k2=λ(λ为常数),则当λ= 0 时,直线MN的斜率k=(定值);当λ ̸=0 时,直线MN恒过定点
证明设A(x1,y1),B(x2,y2),M(xM,yM),N(xN,yN),则相减并整理, 得·(y1+y2) =2p.又由条件知,y1+y2=2yM,则·yM=p,即+pm= 0.同理可得+pm=0.这表明点M,N的轨迹方程为y2−px −ny+pm= 0.平移坐标轴, 把原点移至P(m,n),以x=x′+m,y=y′+n代入上式,得(y′+n)2−p(x′+m)−n(y′+n)+pm=0,即y′2−(px′−ny′)=0.设直线MN的方程为ux′+vy′=1,代入上式,使之成为关于x′、y′的二次齐次方程y′2−(px′ −ny′)(ux′+vy′) = 0,整理得(1 +nv)y′2−(pv −nu)x′y′ −pux′2= 0, 化 为−pu= 0.易知直线AB(即PM),CD(即PN) 的斜率k1,k2为其两根, 据韦达定理,得k1+k2=则当λ= 0 时,k1+k2=0⇒pv −nu=0⇒直线MN的斜率k=(平移不改变直线的斜率); 当λ ̸= 0 时, 有λ ⇒u(−n)+v(p −nλ)=λ ⇒−n)=1⇒直线MN恒过定点(在新坐标系中)⇒直线MN恒过定点(m −)(在原坐标系中).证毕.
特别地,当p= 1,m=n= 1,λ= 1 时,直线MN恒过定点(0,1).这就是上述试题第(2)小题的答案.
2 横向拓展: 由抛物线到椭圆、双曲线的拓展
以上性质揭示了抛物线共定点的两动弦中点连线的一个性质,那么,椭圆、双曲线是否具有类似性质? 经探究,对于椭圆=1(a >b >0),有
性质2.1已知椭圆= 1(a >b >0), 过不在椭圆上的定点P(m,n)分别作斜率为k1,k2的椭圆的动弦AB,CD,设M,N为线段AB,CD的中点,若k1+k2=λ(λ为常数),则当λ= 0 时,直线MN的斜率k=(定值);当λ ̸=0 时,直线MN恒过定点
证明设A(x1,y1),B(x2,y2),M(xM,yM),N(xN,yN),则相减并整理, 得又由条件知,x1+x2=2xM,y1+y2=2yM,则= 0.同理可得这表明点M,N的轨迹方程为b2x2+a2y2−b2mx −a2ny= 0.平移坐标轴,把原点移至P(m,n),以x=x′+m,y=y′+n代入上式,得b2(x′+m)2+a2(y′+n)2−b2m(x′+m)−a2n(y′+n)=0.即b2x′2+a2y′2+(b2mx′+a2ny′)=0.设直线MN的方程为ux′+vy′=1,代入上式,使之成为关于x′、y′的二次齐次方程b2x′2+a2y′2+(b2mx′+a2ny′)(ux′+vy′) = 0,整理得b2(1+mu)x′2+a2(1+nv)y′2+(a2nu+b2mv)x′y′=0,化为
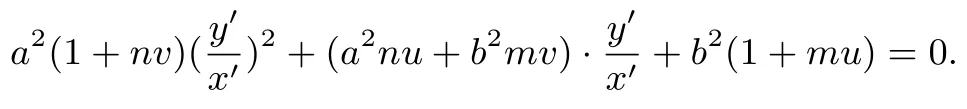
易知直线AB(即PM),CD(即PN)的斜率k1,k2为其两根,据韦达定理得
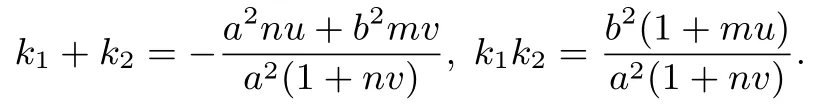
则当λ= 0 时,k1+k2= 0⇒a2nu+b2mv= 0⇒直线MN的斜率k=(平移不改变直线的斜率);当λ ̸=0 时
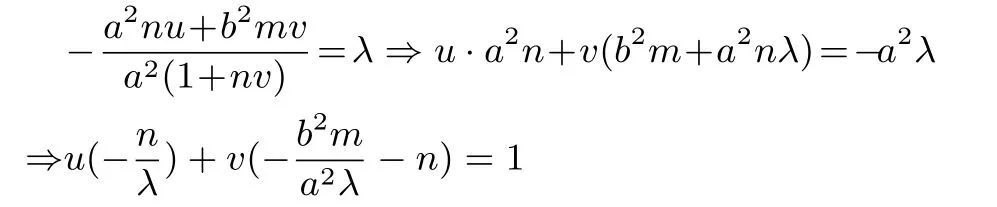
⇒直线MN恒过定点(在新坐标系中)
⇒直线MN恒过定点(在原坐标系中).证毕.
对于双曲线E:= 1(a >0,b >0),只要把上述证明中的“b2”替换为“−b2”,容易得到
性质3.1已知双曲线E:= 1(a >0,b >0),过不在双曲线上的定点P(m,n) 分别作斜率为k1,k2的双曲线的动弦AB,CD, 设M,N为线段AB,CD的中点,若k1+k2=λ(λ为常数), 则当λ= 0 时, 直线MN的斜率k=(定值) ; 当λ ̸= 0 时, 直线MN恒过定点
3 变式拓展: 由“k1+k2 =λ”到“k1k2 =λ”的拓展
以上性质揭示了抛物线、椭圆、双曲线在“k1+k2=λ”条件下的共定点两动弦中点连线的一个性质,如果把该条件变为“k1k2=λ”,会有什么相应的结论?
由性质1.1 的证明, 可得k1k2=若k1k2=λ(λ为非零常数),则=λ ⇒u·0+v(−p −nλ)=λ ⇒ u ·0 +−n) = 1⇒直线MN恒过定点−n)(在新坐标系中)⇒直线MN恒过定点)(在原坐标系中).由此可得
性质1.2已知抛物线y2= 2px(p >0), 过不在抛物线上的定点P(m,n)分别作斜率为k1,k2的抛物线的动弦AB,CD, 设M,N为线段AB,CD的中点, 若k1k2=λ(λ为非零常数),则直线MN恒过定点
由性质2.1 的证明, 可得k1k2=若k1k2=λ(λ为非零常数),则=λ ⇒u·b2m+v(−a2nλ)=a2λ −b2.当λ=时,u·b2m+v(−a2nλ)=0⇒直线MN的斜率k=(平移不改变直线的斜率);当λ ̸=时,直线MN恒过定点(在新坐标系中)⇒直线MN恒过定点(在原坐标系中).由此可得
性质2.2已知椭圆= 1(a >b >0), 过不在椭圆上的定点P(m,n) 分别作斜率为k1,k2的椭圆的动弦AB,CD, 设M,N为线段AB,CD的中点, 若k1k2=λ(λ为非零常数), 则当λ=时, 直线MN的斜率k=(定值) ; 当λ ̸=时, 直线MN恒过定点
类似可得:
性质3.2已知双曲线E:= 1(a >0,b >0),过不在双曲线上的定点P(m,n)分别作斜率为k1,k2的双曲线的动弦AB,CD, 设M,N为线段AB,CD的中点, 若k1k2=λ(λ为非零常数), 则当λ=时, 直线MN的斜率k=(定值);当λ ̸=时,直线MN恒过定点
以上通过对一道全国大联考试题的纵向、横向和变式的探究拓展,得到了抛物线、椭圆和双曲线的一类性质,揭示了问题的本质和规律.这确实是一道值得探究拓展的试题,正如著名数学教育家G·波利亚所形象比喻的:“好问题同某种蘑菇有些相像,它们都成堆地成长,找到一个以后,你应当在周围找一找,很可能附近有好几个.”对一些典型的试题,引导学生进行归纳、类比、联想、发散等拓展探究,获得一系列有价值的结论,这既是对原问题的深化与拓展,也是培养学生创新能力的有效途径.经历丰富多彩的充分探究,主动反思、合作交流等探究过程,学生的创造意识和创新思维能力以及数学学科核心素养就在不知不觉中得到培养和提升.

