选取角为自变量解题

云南省玉溪第一中学(653100) 武增明

选取以角为自变量解题,是高中数学解题的一种常用方法,但多数同学往往想不到、用不上.选取以角为自变量的解题方法,有着十分广泛的运用,如: 求点的横坐标或纵坐标的取值范围(最值),求圆锥曲线离心率的取值范围(最值),求三角形的边长、面积、周长的取值范围(最值),求三角形的两边之和或之差或之积或之商的取值范围(最值),求多面体的体积的取值范围(最值)、求平面凸多边形的边长、面积、周长的取值范围(最值)等等.如何选取角为自变量进行解题研究,以下举例说明,旨在抛砖引玉,以飨读者.

1.求点的横(纵)坐标的取值范围(最值)

例1(2014年高考全国Ⅱ卷理科第16 题) 设点M(x0,1), 若在圆O:x2+y2= 1 上存在点N,使得∠OMN= 45◦,则x0的取值范围是____.

图1

分析选取∠MNO为自变量,记∠MNO=α,应用正弦定理建立x0与α的关系式,问题转化为求角α的三角函数的值域问题.

解因为点M(x0,1) 在直线y= 1 上运动, 记∠MNO=α, 如 图1, 则∠MON+α= 135◦, 所 以0◦ ＜ α ＜135◦, 又因为MO≥ON, 所以在∆MON中知,α≥45◦, 于是45◦≤α ＜135◦.在∆MON中,因为MO=√ON= 1, 所以由正弦定理, 得从而问题转化为求角α的三角函数的值域.因为45◦≤α ＜135◦,所以解之,得−1 ≤x0≤1,从而x0的取值范围是[−1,1].

2.求线段长度的最值(取值范围)

例2在边长为2 的正三角形ABC的边AB,AC上分别取M,N两点,点A关于线段MN的对称点A′正好落在BC边上,则AM长度最小值为____.

分析连接A′M, 如图2, 因为AM=A′M, 所以问题转化为求A′M长度的最小值.在∆BMA′中, 因 为∠B= 60◦,又 设AM=x, 则A′M=x,BM= 2−x, 选取∠BA′M为自变量, 记∠BA′M=θ, 运用正弦定理建立x与θ的关系式,问题又转化为求x关于角θ的三角函数的最值问题.

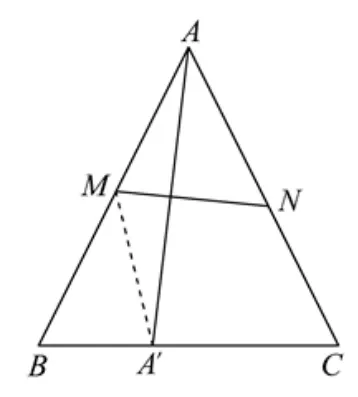
图2

解连接A′M, 如图2, 设AM=x, 则A′M=x,BM= 2−x, 记∠BA′M=θ, 则在∆BMA′中, 因为∠B= 60◦,所以∠BMA′+θ= 120◦,所以0◦＜θ ＜120◦.由正弦定理, 得从而因为0◦＜θ ＜120◦,所以即所以当θ= 90◦, 即∠BA′M=90◦时,AM长度取得最小值为

3.求平面凸多边形的边长的取值范围(最值)

例3(2015年高考全国I 卷理科第16 题)在平面四边形ABCD中,∠A=∠B=∠C=75◦,BC=2,则AB的取值范围是____.

解析连接BD, 如图3, 记∠BDC=θ,选取角θ为自变量,运用正弦定理建立AB与角θ的关系式.在∆BCD中, 由正弦定理, 得在∆ABD中,由正弦定理,得于是故AB=即AB=

图3

在∆BDC中,因为∠C=75◦,所以∠DBC+θ=105◦,又0◦＜∠DBC ＜75◦, 所以0◦＜105◦−θ ＜75◦, 于是30◦＜θ ＜105◦.当θ= 90◦时,AB=√当θ ̸= 90◦时,AB=(30◦＜θ ＜90◦或90◦＜θ ＜105◦),此时,综上,即AB的取值范围是

评注(1)选取∠BAC为自变量也可以.(2)此题解法较多,详见文[1].

4.求平面凸多边形面积的取值范围(最值) [3]

例4如图4, 圆O的直径为2,A为直径延长线上一点, 且OA= 2,B为半圆周长上任意一点,以AB为边作等边∆ABC,问B点在什么位置时,四边形OACB的面积最大,并求出这个最大面积.

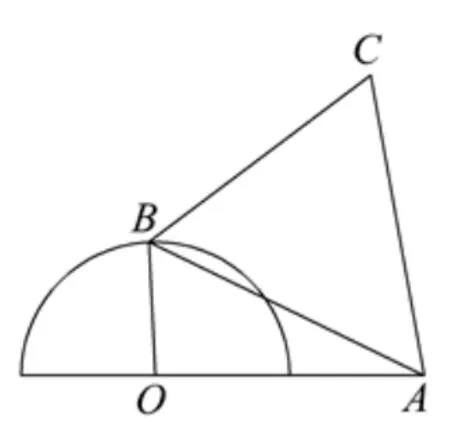
图4

解选取∠AOB为自变量,记∠AOB=x,则S∆AOB=×1×2 sinx=sinx.在∆AOB中,由余弦定理,得AB2=12+22−2×1×2 cosx=5−4 cosx,所以S∆ABC=(5−4 cosx),于是

从而当x=时,S四边形OACB有最大值2+

评注(1)确定B点的位置的方法有两种,方法1 是求B的坐标,方法2 是求∠AOB的大小.(2)由于要用变量表示四边形的面积,所以选取∠AOB为自变量求解较为便捷.

5.求三角形面积的取值范围(最值)

例5(2019年高考全国Ⅲ卷文理科第18 题) ∆ABC的内角A,B,C的对边分别为a,b,c, 已知=bsinA.

(1) 求B; (2) 若∆ABC为锐角三角形, 且c= 1, 求∆ABC面积的取值范围.

解析(1)B=60◦(过程略).

(2) 角A,C都是变量, 在这里选取角C为自变量.由题设及(1)知,∆ABC的面积S∆ABC=由此知问题转化为求边a的取值范围.由(1) 知,A+C= 120◦, 由正弦定理,得a=由此知问题又转化为求三角函数的值域.由于∆ABC为锐角三角形,故0◦＜A ＜90◦,0◦＜C ＜90◦.结合A+C= 120◦,得30◦＜C ＜90◦,所以＜a ＜2,从而因此,∆ABC面积的取值范围是

6.求三角形两边之积的最值(取值范围)

例6[2]已知线段AB= 24,直线l//AB,且直线l到直线AB的距离为5,P为直线l上任意一点,则|PA|·|PB|的最小值为____.

图5

解析选取∠APB为自变量,记∠APB=α, 则运用三角形的面积公式, 利用等面积法思维, 建立|PA| · |PB|与角α的关系式,问题转化为求角α的三角函数的最小值问题.如图5, 根据三角形的面积公式, 可得·AB·h,即|PA|·|PB|sinα=24×5,所 以|PA| · |PB|=(0＜α ＜π).故当α=时,|PA|·|PB|取得最小值120.

7.求圆锥曲线离心率的取值范围(最值)

例7已知双曲线= 1(a ＞0,b ＞0)的左、右焦点分别为F1,F2,若在双曲线的右支上存在一点P,使得|PF1|=3|PF2|,则双曲线离心率e的取值范围是____.

解析为了书写方便,不妨记|PF1|=m,|PF2|=n.选取∠F1PF2为自变量,记∠F1PF2=θ,则解得在∆F1PF2中, 由余弦定理得(2c)2=9a2+a2−6a2cosθ, 所以cosθ=故问题转化为求角θ的三角函数cosθ的值域.因为0＜θ≤π, 所以−1 ≤cosθ ＜1,故−1 ≤＜1,解得1＜e≤2,故双曲线离心率e的取值范围是(1,2].

评注用此法求解此题, 不是最简捷, 笔者认为运用如下性质求解速度快,|PF1|≥a+c,|PF2|≥c −a,|PF1|+|PF2|≥|F1F2|.笔者在这里用此法求解此题,旨在与同仁一道体验选取角为自变量来解题的过程.

8.求多面体体积的最值(取值范围)

例8已知P,A,B,C是半径为2 的球面上的点,PA=PB=PC= 2, ∠ABC=点B在AC上的射影为D,则三棱锥P −ABD体积的最大值为____.

解析由PA=PB=PC知点P在平面ABC上的射影E是∆ABC的外心, 如图6,PE ⊥平面ABC,PE ⊥AC, 又∠ABC=因此E是AC的中点,延长PE交球面于F,连接AF,则∠PAF=,PF是球的直径,PF=2×2=4.

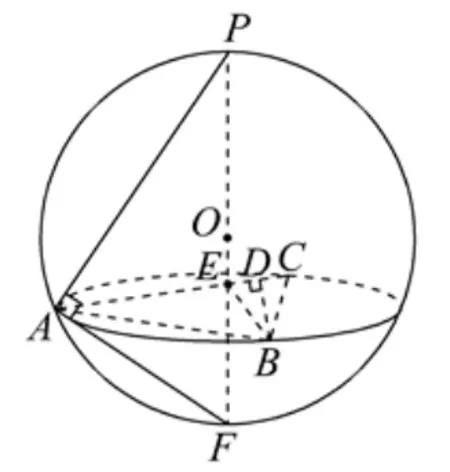
图6

因 为PA2=PE · PF, 所 以PE= 1,AE=故AC= 2AE=在Rt∆ABC中,选取∠BAC为自变量,记∠BAC=θ,则cosθ=所以AB=又sinθ=cosθ=故BD=AD=所以

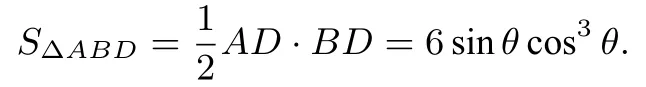
令sin2θ=x(0＜x ＜1), 则三棱锥P −ABD的体积为令f(x)=x(1−x)3(0＜x ＜1),通过求导可解得Vmax=即三棱锥P −ABD的体积的最大值为

究竟怎样选取自变量角解题? 通过以上几例的解答,我们可以发现,要先找出题设中的变量,然后确定变量中的角为自变量,再从多个变量角中选取一个变量角为自变量,结合正弦定理、余弦定理、三角公式、三角形的面积公式、三角函数等相关知识点,建立所求取值范围(最值)的变量与所选取自变量角的关系式,由此把问题转化为求所选取自变量角的三角函数的值域(最值)问题,同时要注意所选取自变量角的取值范围.