一个二元条件极值问题的解法探析
安徽省芜湖市第一中学(241000) 刘海涛
《中国高考评价体系》指出:“高考要求学生能够触类旁通、融会贯通,既包括同一层面、横向的交互融合,也包括不同层面之间、纵向的融会贯通”.在教学过程中,对于一些典型问题,如果我们能够从不同角度思考,寻求不同的解法,以一题多解的方式寻求知识间的内在联系,构建知识的网络体系,加深对问题的本质认识,定会拓宽解题视野,发散解题思维,提升学习兴趣,提高解题能力.在清华大学2020年9月举办的中学生标准学术能力测试中,有一道二元二次函数最值题,笔者从四个角度予以分析,给出8 种解法,现与读者分享交流.
1 试题呈现与分析
题目(2020 清华中学生标准能力测试理科第16 题)已知实数x,y满足4x+y+2xy+1=0,则x2+y2+x+4y的最小值为____.
分析该题形式上以二元二次方程为背景命题,主要考查分析、解决二元二次问题的能力,强化对转化与化归、函数与方程、消元与不等式求最值等数学思想方法的考查,体现了逻辑推理、数学运算、直观抽象等数学核心素养.试题结构虽简单、明了,但内涵丰富[2],值得研究,以发挥该题的最大价值.
2 解法探究
角度一: 借助不等式,化等式为不等式求出最值
解法1(消元+基本不等式法)由4x+y+2xy+1=0得y=则


评注化二元为一元是解决二元函数的最直接做法,通法是消去其中一个变量,得到关于另一变量的函数,接着利用不等式、对勾函数、求导等求出最值.
解法2(因式分解+基本不等式法)由4x+y+2xy+1=0 得(2x+1)(y+2)=1,则
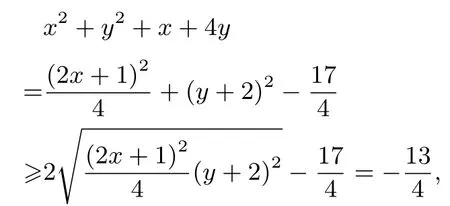
评注通过代数化简, 发现问题可转化关于2x+1 与y+2 的问题,特征为积为定值,求关于平方和的最小值,自然借助基本不等式求最值.
解法3(配凑+基本不等式法)设
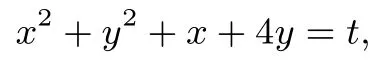
又4x+y+2xy+1=0,则t −1=(x+y)2+5(x+y),即而
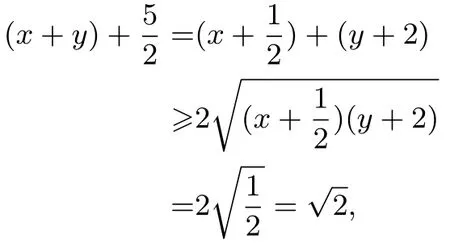
当且仅当x+=y+2 时取等号, 所以t+≥2, 即t≥故x2+y2+x+4y取最小值
评注发现目标式中的与条件式中的相加恰好凑成完全平方式,接着利用基本不等式求出(x+y)+的范围,最后得到答案.
角度二: 借助三角,转化为三角函数最值题
解法4(三角换元法)设

由
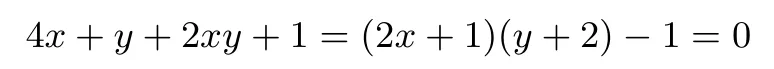
知x+与y+2 均不为零,再设代入(2x+1)(y+2)−1=0,得a2sin 2θ=1,即a2=当θ=kπ+(k ∈Z)时a2取最小值为1,故x2+y2+x+4y取最小值
评注着眼于目标式的特征,三角换元带入条件式,得到利用三角函数的取值范围得到a2的最小值.
角度三: 数形结合,挖掘问题几何背景
解法5(换元+数形结合法)设u=x+,v=y+2,则uv=,x2+y2+x+4y=u2+v2−,再设u2+v2=a2,则问题转化为求a2−的最小值.
如图, 容易知道动圆u2+v2=a2与双曲线uv=相切,对应着a2的最小值, 设切点为(u0,v0),则公切线有两种表示方程:u0u+v0v=a2,u0v+v0u=1, 则相切时a2= 1, 即所以故x2+y2+x+4y的最小值为

评注在解法2 的基础上, 换元后根据式子特征, 发现问题可以转化为动圆与双曲线有公共点的问题, 结合图像不难发现相切为所求最小值对应情形.另外,二次曲线Ax2+Bxy+Cy2+Dx+Ey+F=0 以其上点(x0,y0)为切点的切线方程是Ax0x+
角度四: 回归函数本质,多元函数找对策
解法6(函数偏导法)设

对x求导得
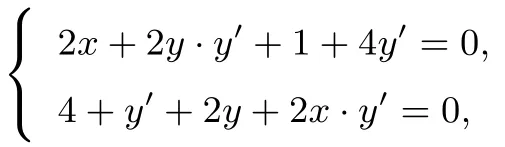
解得x=y=−2, 此时t=故x2+y2+x+4y的最小值为
解法7(拉格朗日乘数法)设函数
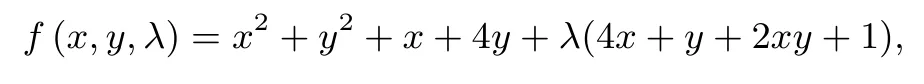
令f(x,y,λ)对x,y,λ的一阶偏导数为零,则

解得

经验证, 当x=−2,λ=−1 或x=−2,λ=−1 时x2+y2+x+4y取最小值
评注函数偏导法与拉格朗日乘数法都是是高等数学背景下的解法,提供给读者参考.
3 教学启示
数学解题的目的是什么? 是求出问题的答案吗? 是,但不全是! 解题的目的是巩固数学基础知识、落实数学基本技能、感悟数学思想方法、提升数学思维活动经验,所以对一道典型问题的多角度分析与解答是非常有必要的.用多种方法解答同一道数学题, 不仅能更牢固地掌握相关的数学知识,还能更灵活地运用所学知识.通过一题多解,分析、比较各种解法,可以找到最佳的解题途径,从而发散学生的思维能力,对巩固知识和解题能力大有裨益,是提高数学成绩的一条捷径[3].但是我们在日常学习中,要结合自身掌握程度和实际情况,选择最佳的解题方法,不要一味追求某一种解法,要学会从不同解法中汲取不同的数学思想,提高自身的数学核心素养[4].

